§4. Математический анализ бесконечного

1.Основные понятия. Последовательность натуральных чисел

1, 2, 3, . . .

представляет собой первый и самый важный пример бесконечного множества. Не нужно видеть ничего таинственного в том, что она — бесконечная, что у нее «нет конца»: как бы велико ни было натуральное число n, можно построить другое, следующее за ним число, еще большее — n + 1. Но при переходе от прилагательного «бесконечный», означающего просто-напросто «не имеющий конца», к существительному «бесконечность» никоим образом не следует привносить допущения, что «бесконечность», обыкновенно изображаемая особым символом ∞, может быть рассматриваема как обыкновенное число. Нельзя включить символ ∞ в числовую систему действительных чисел, не нарушая при этом основных законов арифметики. И тем не менее идея бесконечности пронизывает всю математику, так как математические объекты изучаются обыкновенно не как индивидуумы — каждый в отдельности, а как члены классов или совокупностей, содержащих бесчисленное множество элементов одного и того же типа; таковы совокупности натуральных чисел, действительных чисел или же треугольников на плоскости. Именно по этой причине возникает необходимость в точном математическом анализе бесконечного. Современная теория множеств, созданная Георгом Кантором и его школой в конце XIX столетия, приступив к разрешению этой задачи, достигла значительных успехов. Канторова теория множеств глубоко проникла во многие области математики и оказала на них огромное влияние; она стала играть особо выдающуюся роль в исследованиях, связанных с логическим и философским обоснованием математики. Исходным в канторовой теории является общее понятие совокупности или множества. При этом имеется в виду собрание объектов (элементов), которое определяется некоторым правилом, позволяющим с полной определенностью судить о том, входит ли данный объект в число элементов собрания или не входит. Примерами могут служить множество всех натуральных чисел, множество всех периодических десятичных дробей, множество всех действительных чисел или множество всех прямых в трехмерном пространстве.

Для того чтобы сравнивать множества с точки зрения «количества» содержащихся в них элементов, нужно ввести основное в этой теории понятие «эквивалентности» множеств. Если элементы двух множеств A и B могут быть приведены в попарное соответствие такого рода, что каждому элементу множества A сопоставлен один и только один элемент множества B, а каждому элементу множества B сопоставлен один и только один элемент множества A, то установленное таким образом соответствие называется взаимно однозначным, а о самих множествах A и B

тогда говорят, что они между собой эквивалентны. Понятие эквивалентности в случае конечных множеств совпадает с обыкновенным понятием числового равенства, так как два конечных множества в том и только том случае могут быть приведены во взаимно однозначное соответствие, если содержат одно и то же число элементов. На этом и основывается, нужно заметить, идея счета: когда мы «считаем» элементы множества, то процесс счета как раз и заключается в установлении взаимно однозначного соответствия между элементами множества и числами 1, 2, . . . , n.

Чтобы установить эквивалентность двух конечных множеств, иногда нет необходимости «считать» элементы. Так, например, не считая, можно утверждать, что конечное множество кругов единичного радиуса эквивалентно множеству их центров.

Перенося понятие эквивалентности на бесконечные множества, Кантор имел в виду создать «арифметику» бесконечного. Множество действительных чисел и множество точек на прямой линии эквивалентны, так как после того, как выбраны начало и единичный отрезок, данная прямая становится «числовой прямой», и каждой ее точке P в качестве координаты взаимно однозначно сопоставляется некоторое совершенно определенное действительное число x:

P ↔ x.

Четные числа образуют правильное подмножество множества всех

натуральных чисел, а все целые числа образуют правильное подмножество множества всех рациональных чисел. (Говоря о «правильном» подмножестве некоторого множества S, мы имеем в виду множество S0, состоящее из элементов множества S, но не из всех его элементов.) Совершенно ясно, что если данное множество конечно, т. е. содержит какое-то число n элементов и не более того, то оно не может быть эквивалентно никакому своему правильному подмножеству, так как всякое правильное его подмножество содержало бы самое большее n − 1

элемент. Но если данное множество содержит бесконечное число элементов, то, как это ни парадоксально, оно может быть эквивалентно некоторому своему правильному подмножеству. Например, схема

устанавливает взаимно однозначное соответствие между множеством натуральных чисел и множеством всех четных целых положительных чисел, и эти два множества оказываются эквивалентными, хотя второе есть правильное подмножество первого. Такое противоречие с ходячей истиной «целое больше своей части» показывает, какие сюрпризы нас ждут в области «арифметики бесконечного».

2. Счетность множества рациональных чисел и несчетность континуума. Одно из первых открытий Кантора в области анализа бесконечного заключалось в том, что множество рациональных чисел (содержащее в качестве правильного подмножества бесконечное множество натуральных чисел и потому само бесконечное) эквивалентно множеству натуральных чисел. На первый взгляд кажется странным, что всюду плотное множество рациональных чисел не более богато элементами, чем множество натуральных чисел, элементы которого «рассеяны» редко и стоят на значительном расстоянии один от другого. И в самом деле, с сохранением порядка возрастания нельзя расположить положительные рациональные числа так, как это можно сделать с натуральными: самое маленькое число a будет первым, следующее за ним по величине b вторым, и т. д.; дело в том, что рациональные числа расположены везде плотно, и потому ни для одного из них нельзя указать «следующего по величине». Но Кантор заметил, что если отказаться от требования «располагать по величине», то тогда оказывается возможным расставить все рациональные числа в ряд r1, r2, r3, r4,

. . ., подобный ряду натуральных чисел. Такое расположение предметов некоторого множества в виде последовательности часто называют пересчетом («нумерацией») этого множества. Множества, для которых пересчет может быть выполнен, называются счетными или исчислимыми. Указывая один из способов пересчета множества рациональных чисел и устанавливая, таким образом, его счетность, Кантор тем самым показал, что это множество эквивалентно множеству натуральных чисел, так как схема

создает взаимно однозначное соответствие между двумя множествами. Мы опишем сейчас один из возможных способов пересчета множества рациональных чисел.

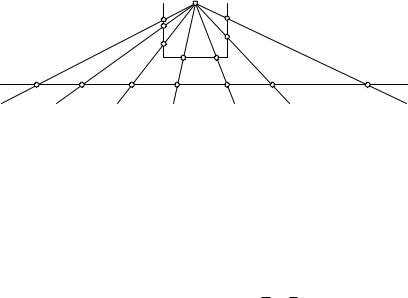
Каждое рациональное число записывается в виде ab , где a и b —

целые числа; все эти числа могут быть расположены в виде таблицы, где число ab стоит в a-м столбце и в b-й строчке. Например, 34 станет

в третьем столбце и в четвертой строчке таблицы. Предположим, что все свободные места, или «клеточки», в таблице заполнены соответствующими числами, а затем проведем по таблице непрерывную ломаную линию, которая пройдет через все клеточки. Начиная с 1, мы сделаем сначала один шаг вправо и получим 2 в качестве второго члена последовательности; затем по диагонали налево и вниз — получим третий член 12 ; следующий шаг прямо вниз даст нам четвертый член 13 ; потом

Раз оказалось, что множество рациональных чисел счетно, то могло бы возникнуть подозрение, что и всякое бесконечное множество также счетно, и на этом, естественно, закончился бы весь анализ бесконечного. Но это совсем не так. Тому же Кантору принадлежит открытие исключительной важности: множество всех действительных (рациональных и иррациональных) чисел несчетно. Другими словами, совокупность всех действительных чисел совершенно иного (так сказать более высокого) «типа бесконечности», чем совокупность одних только целых или одних только рациональных чисел. Принадлежащее Кантору остроумное «косвенное» доказательство этого факта стало моделью для многих иных доказательств в математике. Идея рассуждения такова. Мы исходим из допущения, что все действительные числа удалось перенумеровать, располагая их в виде последовательности, и после этого демонстрируем число, которое никак не может быть числом этой последовательности. Отсюда возникает противоречие: ведь было предположено, что все действительные числа вошли в состав последовательности, и это предположение должно быть признано ложным, если хотя бы одно число оказывается за пределами последовательности. Таким образом обнаруживается несостоятельность утверждения, что все действительные числа поддаются «пересчету», и ничего другого не остается, как только признать вместе с Кантором, что множество действительных чисел несчетно.

Однако проведем это рассуждение фактически. Допустим, что все действительные числа, представленные в виде бесконечных десятичных дробей, расположены в порядке последовательности, или списка:

1-е число N1,a1a2a3a4a5 . . .

2-е число N2,b1b2b3b4b5 . . .

3-е число N3,c1c2c3c4c5 . . .

. . . . . . . . . . . . . . . . . . . . . . . . .

где буквы Ni обозначают целую часть, а буквы a, b, c, . . . представляют собой десятичные знаки, стоящие вправо от запятой. Мы допускаем, что эта последовательность дробей охватывает все действительные числа. Существенной частью доказательства является построение с помощью «диагональной процедуры» такого нового числа, относительно которого можно показать, что оно не входит в наш список.

Построим такое число. Для этого возьмем первую цифру после запятой a, какую угодно, но отличную от a1, а также от 0 и 9 (последнее — чтобы избежать затруднений, возникающих из равенств вроде следующего: 0,999 · · · = 1,000 . . .); затем вторую цифру b возьмем отличной от b2, а также от 0 и 9; третью цифру c — отличной от c3 и т. д. (Для большей определенности можно условиться в следующем: мы берем a =

1, если только a1 6= 1, а в случае a1 = 1 возьмем a = 2; и аналогично для всех прочих цифр b, c, d, e, . . .) Теперь рассмотрим число

z = 0,abcde . . .

Это новое число z наверняка не входит в наш список; действительно, оно не равно первому числу, стоящему в списке, так как от него отличается первой цифрой после запятой, оно не равно второму числу, так как от него отличается второй цифрой после запятой, и вообще отлично от n-го числа по списку, так как от него отличается n-й цифрой после запятой. Итак, в нашем списке, составленном будто бы из всех действительных чисел, нет числа z. Значит, множество всех действительных чисел несчетно.

Рис. 20. Взаимно однозначное соответствие между точками согнутого интервала и точками прямой линии

Читателю может прийти в голову мысль, что несчетность континуума обусловливается неограниченной протяженностью прямой линии и что конечный отрезок прямой будет содержать лишь счетное множество точек. Чтобы убедиться в ложности такого предположения, достаточно установить, что весь числовой континуум в целом эквивалентен некоторому конечному интервалу, скажем, единичному интервалу от 0 до 1. Получить необходимое для этой цели взаимно однозначное соответствие можно, например, сгибая интервал в точках 13 и 23 и затем проектируя

так, как показано на рис. 20. Отсюда видно, что даже конечный интервал (и, конечно, отрезок) содержит несчетное множество точек.

Упражнение. Покажите, что любой отрезок [A, B] числовой прямой эквивалентен любому другому отрезку [C, D] (рис. 21).

Стоит привести еще другое доказательство несчетности континуума, носящее, пожалуй, более интуитивный характер. Достаточно (принимая

больше элементов, чем B. Но если мы заменим понятие «множеств, имеющих одно и то же конечное число элементов» более общим понятием «эквивалентных множеств», то — в случае бесконечных множеств — предыдущее утверждение уже не будет справедливо: множество всех целых чисел содержит «больше» элементов, чем множество всех четных чисел, а множество всех рациональных чисел — «больше» элементов, чем множество всех целых чисел; и, однако, как мы видели, все эти множества эквивалентны. Можно было бы заподозрить, что все бесконечные множества между собой эквивалентны, но Кантор опроверг это предположение: существует множество — континуум действительных чисел, — которое не эквивалентно никакому счетному множеству.

Итак, существует по меньшей мере два различных «типа бесконечности»: счетная бесконечность натуральных чисел и несчетная бесконечность континуума. Если два множества A и B, конечные или бесконечные, эквивалентны, мы скажем, что им соответствует одно и то же кардинальное число (или мощность). В случае конечных множеств кардинальное число сводится к обыкновенному натуральному числу, но понятие кардинального числа носит более общий характер. Далее, если случится, что множество A эквивалентно некоторому подмножеству (части) множества B, но само B неэквивалентно ни множеству A, ни какой бы то ни было его части, то говорят, следуя Кантору, что множеству B соответствует большее кардинальное число, чем множеству A. Это употребление термина «число» также согласуется с обычным употреблением в случае конечных множеств. Множество целых чисел есть подмножество множества всех действительных чисел, тогда как множество действительных чисел не эквивалентно ни множеству целых чисел, ни какому бы то ни было его подмножеству (оно ни счетное, ни конечное). Значит, по данному определению, континууму действительных чисел соответствует большее кардинальное число, чем множеству натуральных чисел.

* Кантор показал фактически, как можно построить бесконечную последовательность бесконечных множеств, которым соответствуют все б´ольшие и б´ольшие кардинальные числа. Так как можно исходить из множества натуральных чисел, то достаточно показать, что, каково бы ни было данное множество A, можно построить другое множество B, у которого кардинальное число будет больше, чем у A. Вследствие большой общности этой теоремы доказательство ее по неизбежности несколько абстрактно. Множество B мы определяем как множество, элементами которого являются все возможные подмножества множества A. Говоря о «подмножествах» A, мы в данном случае имеем в виду не только «правильные подмножества» A, но не исключаем и самого множества A, а также «пустого» множества , не содержащего никаких элементов. (Так, если A состоит из трех целых чисел 1, 2, 3, то B содержит 8 различных элементов {1, 2, 3}, {1, 2}, {1, 3}, {2, 3}, {1}, {2}, {3} и .) Каждый

элемент множества B сам есть множество, состоящее из каких-то элементов множества A. Допустим теперь, что B эквивалентно A или некоторому подмножеству A, т. е. что существует некоторое правило, приводящее во взаимно однозначное соответствие элементы A или некоторого подмножества A со всеми элементами B, т. е. всеми подмножествами A:

где через Sa обозначено то подмножество A, которому соответствует элемент a множества A. Мы придем к противоречию, если укажем некоторый элемент B, т. е. некоторое подмножество T множества A, которому не может соответствовать никакой элемент a. Чтобы построить подмножество T , заметим прежде всего, что для всякого элемента x из A существуют две возможности: либо множество Sx, сопоставляемое зависимостью (2) элементу x, содержит элемент x, либо не содержит. Мы определим T как подмножество A, состоящее из всех таких элементов x, что Sx не содержит x. Определенное таким образом множество T отличается от всякого Sa по крайней мере элементом a, так как если Sa содержит a, то T не содержит a, а если Sa не содержит a, то T содержит a. Итак, T не включено в соответствие (2). Это и показывает, что невозможно установить взаимно однозначное соответствие между элементами A (или некоторого подмножества A) и элементами B. Но соотношение

a ↔ {a}

устанавливает взаимно однозначное соответствие между всеми элементами A и подмножеством B, состоящим из одноэлементных подмножеств A. Значит, по данному выше определению, множеству B соответствует большее кардинальное число, чем множеству A.

* Упражнение. Если множество A содержит n элементов, то определенное выше множество B содержит 2n элементов. Если A есть множество натуральных чисел, то B эквивалентно континууму действительных чисел, заключенных между 0 и 1. (Указание: сопоставьте каждому подмножеству A символ, состоящий из последовательности — конечной в первом примере, бес-

конечной во втором —

a1a2a3 . . . ,

где an = 1 или 0, смотря по тому, принадлежит или не принадлежит n-й элемент A рассматриваемому подмножеству.)

Могло бы показаться легкой задачей построить множество точек, обладающее б´ольшим кардинальным числом, чем множество точек единичного отрезка. Казалось бы, что квадрат со стороной 1, как «двумерная» фигура, должен содержать «больше» точек, чем «одномерный» отрезок. Но, как это ни странно, дело обстоит иначе: кардинальное число точек квадрата в точности равно кардинальному числу точек отрезка. Для доказательства достаточно установить взаимно однозначное соответствие между точками квадрата и точками отрезка. Постараемся это сделать.

Если (x, y) есть какая-нибудь точка единичного квадрата, то ее координаты x и y могут быть представлены в виде десятичных разложений

причем пусть будет условлено (ради избежания всяких сомнений), что, например, число 14 будет записываться в виде 0,25000 . . ., а не в виде 0,24999 . . .

Названной точке квадрата (x, y) мы сопоставим точку единичного отрезка

z = 0,a1b1a2b2a3b3a4b4 . . . .

Очевидно, различным точкам квадрата (x, y) и (x0, y0) сопоставляются различные же точки отрезка z и z0; это и значит, что кардинальное число множества точек квадрата не превышает кардинального числа множества точек отрезка.

(Собственно говоря, в данном случае построено взаимно однозначное соответствие между множеством всех точек квадрата и некоторым подмножеством точек отрезка: никакая точка квадрата не будет соответствовать, например, точке отрезка 0,2140909090 . . ., так как мы условились писать 0,25000 . . ., а не 0,24999 . . . Но можно слегка видоизменить построение таким образом, чтобы действительно осуществлялось взаимно однозначное соответствие между множеством всех точек квадрата и множеством всех точек отрезка.)

Аналогичнее рассуждение показывает, что кардинальнее число точек куба не превышает кардинального числа точек отрезка.

Все эти результаты, казалось бы, стоят в противоречии с интуитивным представлением о «размерности». Но нужно обратить внимание на то, что вводимые нами соответствия не являются «непрерывными»; когда мы перемещаемся по отрезку от 0 к 1 непрерывно, соответствующие точки в квадрате не образуют непрерывной кривой, а будут появляться в порядке совершенно «хаотическом». Размерность множества точек зависит не только от кардинального числа точек, но и от того, как они расположены в пространстве. Мы вернемся к этому вопросу в главе V.

4. Косвенный метод доказательства. Теория кардинальных чисел представляет собой лишь один из аспектов общей теории множеств, созданной Кантором несмотря на суровую критику со стороны наиболее выдающихся математиков того времени. Многие из критиков, например Пуанкаре и Кронекер, возражали против неопределенности общего понятия «множества» и против неконструктивного характера рассуждений, применявшихся при определении некоторых множеств.

Возражения против неконструктивных рассуждений относятся к тем доказательствам, которые можно было бы назвать «существенно косвенными». Сами по себе «косвенные» доказательства есть самый обыкновенный элемент математического мышления: желая установить истинность предложения A, мы вначале допускаем, что справедливо иное предложение A0, противоположное A; затем некоторая цепь рассуждений приводит нас к утверждению, противоречащему A0, и тем самым обнаруживается несостоятельность предложения A0. Тогда на базе основного логического принципа «исключенного третьего» из ложности A0 следует истинность A.

В разных местах этой книги читатель найдет ряд таких примеров,

для которых косвенное доказательство легко может быть превращено в прямое, но «косвенная» форма создает преимущества краткости и освобождает от рассмотрения подробностей, имеющих второстепенный интерес с точки зрения поставленной ближайшей цели. Но попадаются и такие теоремы, для которых до настоящего времени не удалось дать иных доказательств, кроме косвенных. О некоторых из этих теорем можно даже сказать, что, по-видимому, по самой их природе прямые, конструктивные их доказательства принципиально невозможны. Сюда относится, например, теорема, приведенная на стр. 102. Не раз бывали случаи в истории математики, когда все усилия математиков были направлены в сторону построения («конструкции») решения тех или иных проблем, разрешимость которых предполагалось установить, а затем кто-нибудь приходил, если так можно выразиться, со стороны и ликвидировал все трудности с помощью «косвенного» неконструктивного рассуждения.

Когда речь идет о доказательстве существования объекта определенного типа, то имеется существенное различие между тем, чтобы построить осязаемый пример объекта, и тем, чтобы доказать, что из несуществования объекта можно вывести противоречивые заключения. В первом случае получается осязаемый объект, во втором — ничего, кроме противоречия. Не так давно некоторые математики (весьма заслуженные) провозгласили более или менее полное устранение из математики всех неконструктивных доказательств. Даже если бы выполнение этой программы признать желательным, необходимо указать, что это повлекло бы за собой в настоящую эпоху чрезвычайные усложнения, и можно было бы даже опасаться, что в процессе совершающихся потрясений подверглись бы разрушению существенные части организма математики. Поэтому нечего удивляться, что школа «интуиционистов», принявшая упомянутую программу, встретила упорное сопротивление, и что даже наиболее ортодоксальные интуиционисты не всегда в состоянии жить согласно своим убеждениям.1

5. Парадоксы бесконечного. Хотя бескомпромиссная позиция, занятая интуиционистами, с точки зрения большинства математиков является слишком экстремистской, волей-неволей приходится согласиться, что для внешне прекрасной теории бесконечных множеств возникла серьезная угроза, когда в пределах самой этой теории обнаружились совершенно явные логические парадоксы. Очень скоро было замечено, что неограниченная свобода в пользовании понятием «множество» неиз-

1Об интуиционизме и выросшем из него конструктивном направлении в математике и логике, на исчерпывающую характеристику которых никак не претендуют эти строки, см., например, [11] и [15] в списке литературы в конце книги (номера по которому всюду указываются в квадратных скобках). — Прим. ред.

бежно ведет к противоречиям. Мы приведем здесь один из парадоксов, обнаруженный Бертраном Расселом. Вот в чем он заключается.

Как правило, множества не содержат себя в качестве элемента. Например, множество A всех целых чисел содержит в качестве элементов только целые числа; так как само A не есть целое число, а есть множество целых чисел, то A себя в качестве элемента не содержит. Условимся называть такие множества «ординарными». Но могут существовать и такие множества, которые содержат себя в качестве элемента. Рассмотрим, например, множество S, определенное следующим образом: «S содержит в качестве элементов все множества, которые можно определить посредством предложения, содержащего меньше двадцати слов». Так как само множество S определяется предложением, содержащим меньше двадцати слов, то выходит, что оно является элементом множества S. Такие множества назовем «экстраординарными». Как бы то ни было, большинство множеств — ординарные; попробуем не иметь дела с дурно ведущими себя экстраординарными множествами и будем рассматривать только множество всех ординарных множеств. Обозначим его буквой C. Каждый элемент C есть множество, притом ординарное множество. Но вот возникает вопрос: а само множество C —

ординарное или экстраординарное? Несомненно, оно должно быть или тем, или другим.1 Если C — ординарное множество, то оно содержит себя в качестве элемента, так как C определено как множество всех ординарных множеств. Раз дело обстоит так, значит, C — экстраординарное множество, так как экстраординарными, согласно определению, названы множества, содержащие себя в качестве элемента. Получается противоречие. Значит, C должно быть экстраординарным множеством. Но тогда множество C содержит в качестве элемента себя, т. е. оно есть экстраординарное множество, а это противоречит определению C как множества всех ординарных множеств. Итак, мы видим, что уже одно только допущение существования множества C внутренне противоречиво.

6. Основания математики. Парадоксы вроде вышеприведенного побудили Рассела и других подвергнуть систематическому изучению основания математики и логики. Конечная цель этих исследований заключается в создании для математических рассуждений такой логической базы, относительно которой можно было бы доказать, что она свободна от возможных противоречий, и которая вместе с тем была бы достаточно обширной, чтобы из нее можно было путем дедукции

1Получаемое далее противоречие может быть выведено и без использования так называемого закона исключенного третьего, подразумеваемого в этой фразе. См., например, Френкель А. и Бар-Хиллел И. Основания теории множеств. — М.: Мир, 1966, гл. I, § 2. — Прим. ред.