
- •К русскому читателю
- •Как пользоваться книгой
- •Что такое математика?
- •Натуральные числа
- •Введение
- •Операции над целыми числами
- •Бесконечность системы натуральных чисел. Математическая индукция
- •Введение
- •Математическая числовая система
- •Введение
- •Рациональные числа
- •Несоизмеримые отрезки. Иррациональные числа, пределы
- •Рациональные числа и периодические десятичные дроби.
- •Замечания из области аналитической геометрии
- •Математический анализ бесконечного
- •Комплексные числа
- •Алгебраические и трансцендентные числа
- •Геометрические построения. Алгебра числовых полей
- •Введение
- •Основные геометрические построения
- •Неразрешимость трех классических проблем
- •Геометрические преобразования. Инверсия
- •Построения с помощью других инструментов. Построения Маскерони с помощью одного циркуля
- •Еще об инверсии и ее применениях
- •Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- •Введение
- •Основные понятия
- •Двойное отношение
- •Параллельность и бесконечность
- •Применения
- •Аналитическое представление
- •Конические сечения и квадрики
- •Аксиоматика и нееклидова геометрия
- •Топология
- •Введение
- •Формула Эйлера для многогранников
- •Топологические свойства фигур
- •Другие примеры топологических теорем
- •Топологическая классификация поверхностей
- •Приложение
- •Функции и пределы
- •Введение
- •Независимое переменное и функция
- •Пределы
- •Пределы при непрерывном приближении
- •Точное определение непрерывности
- •Две основные теоремы о непрерывных функциях
- •Теорема Вейерштрасса об экстремальных значениях.
- •Некоторые применения теоремы Больцано
- •Максимумы и минимумы
- •Введение
- •Задачи из области элементарной геометрии
- •Общий принцип, которому подчинены экстремальные задачи
- •Стационарные точки и дифференциальное исчисление
- •Треугольник Шварца
- •Проблема Штейнера
- •Экстремумы и неравенства
- •Существование экстремума. Принцип Дирихле
- •Экстремальные проблемы элементарного содержания.
- •Изопериметрическая проблема
- •Вариационное исчисление
- •Вариационное исчисление. Принцип Ферма в оптике.
- •Экспериментальные решения задач на минимум. Опыты с мыльными пленками
- •Математический анализ
- •Введение
- •Интеграл
- •Примеры интегрирования. Интегрирование функции xr.
- •Производная
- •Техника дифференцирования
- •Обозначения Лейбница и «бесконечно малые»
- •Основная теорема анализа
- •Определение и свойства логарифма. Эйлерово число e.
- •Дифференциальные уравнения
- •Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- •Дополнительные замечания. Задачи и упражнения
- •Арифметика и алгебра
- •Аналитическая геометрия
- •Геометрические построения
- •Проективная и неевклидова геометрия
- •Топология
- •Функции, пределы, непрерывность
- •Максимумы и минимумы
- •Дифференциальное и интегральное исчисления
- •Техника интегрирования
- •О создании книги «Что такое математика?»
- •Рекомендуемая литература
- •Предметный указатель

338 |
ФУНКЦИИ И ПРЕДЕЛЫ |
гл. VI |
поведение функции f(x) только при больших положительных значениях, то условие |x| > K мы должны заменить условием x > K; напротив, для случая больших по абсолютной величине отрицательных значений x вводим условие x < −K. Чтобы символизировать эти два способа «одностороннего» стремления к бесконечности, мы пишем, соответственно,
x → +∞, x → −∞.
§4. Точное определение непрерывности
В§ 1, пункт 5, мы ввели следующее определение непрерывности функции: функция f(x) непрерывна в точке x = x1, если при стремлении x к x1 величина f(x) стремится к пределу, равному f(x1). Если мы проанализируем эту формулировку, то увидим, что она подразумевает выполнение следующих двух требований:
а) существует предел a функции f(x) при стремлении переменной x
кx1,
б) этот предел a должен быть равен f(x1).
Если в определении предела на стр. 326 мы подставим вместо a его значение f(x1), то условие непрерывности принимает следующий вид:
функция f(x) непрерывна при x = x1, если, как бы мало ни было положительное число e, можно подобрать такое положительное число d (зависящее от e), что неравенство
|f(x) − f(x1)| < e
будет выполнено для всех x, удовлетворяющих условию
|x − x1| < d
(ограничение x 6= x1, введенное в определении предела, здесь излишне, поскольку неравенство |f(x) − f(x1)| < e при x = x1 удовлетворяется автоматически).
В качестве примера постараемся установить непрерывность функции f(x) = x3, скажем, в точке x1 = 0. Мы имеем
f(x1) = 03 = 0.
Выберем теперь маленькое положительное число e, например, e = 10001 .
Мы должны показать, что, ограничивая значения x числами, достаточно близкими к 0, получим соответствующие значения функции f(x),
отличающиеся от 0 меньше, чем на 10001 , т. е. заключенные между −10001
и + 10001 . Мы сразу видим, что значения f(x) не выйдут из этих границ, если мы ограничим изменение x значениями, отличающимися от 0 мень-
r
ше чем на d = 3 |
|
1 |
= |
|
1 |
; в самом деле, если |x| < |
|
1 |
, то |f(x)| = |x3| < |
1000 |
10 |
10 |
|||||||
§ 4 |
|
ТОЧНОЕ ОПРЕДЕЛЕНИЕ НЕПРЕРЫВНОСТИ |
|
339 |
||||||||
1 |
. Совершенно так же мы можем взять вместо e = |
1 |
любое мень- |
|||||||||
1000 |
|
4 |
, 10− |
5 |
|
3 |
1000 |
|
|
|||
|
|
|
|
|
|
|
||||||
шее значение e = 10− |
|
и т. д.; числа d = √e будут удовлетворять на- |
||||||||||
шему |
|
|
|
|
|
|
|
|
|
|||
требованию, так как из неравенства |
|
|
|
|
||||||||
|x| |
<3 |
3 |
|
|
|
|
|
|
|
|
|
|
√e следует неравенство |f(x)| = |
u |
|
|
|
||||||||
= |x |
| < e. |
|
|
|
|
|
|
|
|
|
||
|
Основываясь |
на |
определении |
|
|
|
|
|||||
непрерывности с помощью e, d, |
u1 |
|
|
|
||||||||
|
|
2 |
||||||||||
можно доказать аналогично, что все |
|
|
|
|
||||||||
полиномы, рациональные функции и |
|
|
2 |
|
||||||||
тригонометрические функции непре- |
|
|
|
|
||||||||
рывны в любой точке, за исключени- |
|
|
x1 |
x |
||||||||
ем, может быть, тех изолированных |
|
|
|
|
||||||||
значений x, около которых функции |
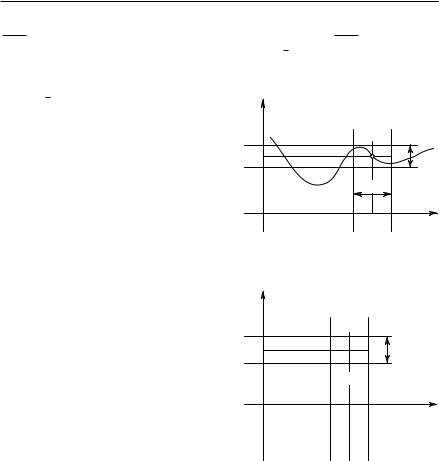
Рис. 170. Функция, непрерывная в |
|||||||||||
становятся бесконечными. |
|
|||||||||||
|
точке x = x1 |
|
||||||||||
|
Связывая определение непрерыв- |
|
|
|
|
|||||||
ности с графиком функции u = f(x), |
u |
|
|
|
||||||||
можно придать ему следующую гео- |
|
|
|
|
||||||||
метрическую форму. Выберем неко- |
|
|
|
|
||||||||
торое положительное число e и на- |
|
|
|
|
||||||||
чертим прямые, параллельные оси x |
|
|
|
|
||||||||
на |
высоте f(x1) − e |
и |
|
f(x1) + e |
|
2 |
|
|
||||
над ней. Тогда должно найтись та- |
|
|
|
|
||||||||
кое положительное число d, что вся |
|
|
|
x |
||||||||
часть графика, лежащая внутри вер- |
|
|
|
|
||||||||
тикальной полоски шириной в 2d око- |
|
|
|
|
||||||||
ло x1, содержится также и в горизон- |
|
|
|
|
||||||||
тальной полоске шириной в 2e око- |
Рис. 171. Функция имеет разрыв в |
|||||||||||
ло f(x1). Рис. 170 показывает функ- |
||||||||||||
точке x = x1 |
|
|||||||||||
цию, непрерывную в точке x1, в то |
|
|||||||||||
|
|
|
|
|||||||||
время как рис. 171 показывает функ- |
|
|
|
|
||||||||
цию, имеющую разрыв в этой точке. В последнем случае, как бы ни |
||||||||||||
была узка вертикальная полоска около x1, она всегда будет содержать |
||||||||||||
часть графика, лежащую вне горизонтальной полоски ширины 2e. |
||||||||||||
Если я утверждаю, что данная функция u = f(x) непрерывна в точке x = x1, то это значит, что я беру на себя по отношению к вам следующие обязательства: вы можете выбрать любое положительное число e, сколь угодно малое, но определенное. Тогда я обязуюсь подыскать такое положительное число d, чтобы неравенство |x − x1| < d влекло за собой неравенство |f(x) − f(x1)| < e. Но при этом я не обязуюсь найти такое число d, которое подошло бы ко всякому e, которое вы назовете потом: мой выбор d зависит от вашего выбора e. Если вы можете выбрать хоть одно e, для которого я не смогу подобрать подходящего d, то моя игра проиграна — мое утверждение опро-
