366 |
МАКСИМУМЫ И МИНИМУМЫ |
гл. VII |
||
качестве упражнения). Но мы видели, что отрезки P R и QR образуют |
||||
одинаковые углы с эллипсом в точке R, и так как эллипс в точке R |
||||
касается кривой C, то отрезки P R и QR образуют в той же точке также |
||||
одинаковые углы и с C. Совершенно аналогичное рассуждение приво- |
||||
дит нас к тому же результату и в случае, если в точке R сумма p + q |
||||
обращается в минимум. |
|
|
||
Итак, мы пришли к теореме: дана замкнутая кривая C и две точ- |
||||
ки P и Q вне ее; |
тогда в каждой из точек R, в которых сумма p + q |
|||
принимает наибольшее или наименьшее значение на кривой C, отрез- |
||||
ки P R и QR образуют одинаковые углы с самой кривой (т. е. с ее |
||||
касательной). |
|
|
|
|
Если точка P внутри C, а точка Q вне C, то теорема остается спра- |
||||
ведливой для той точки, где p + q принимает наибольшее значение, но |
||||
|
|
она теряет смысл для точки, |
||
|
|
где p + q принимает наименьшее |
||
|
|
значение, так как эллипс вырож- |
||
|
|
дается в отрезок прямой. |
||
|
P |
Рассуждая |
аналогичным об- |
|
|
разом (воспользовавшись вместо |
|||
|
|
|||
Q |
|
свойств эллипса свойством гипер- |
||
R |
|
болы), читатель сможет доказать |
||
C |
|
следующую теорему: дана замк- |
||
|
нутая кривая C и две точки P |
|||
|
|
|||
|
|
и Q — одна внутри, другая вне C; |
||
|
|
тогда в каждой из тех точек R |
||
|
|
на C, где разность p − q прини- |
||
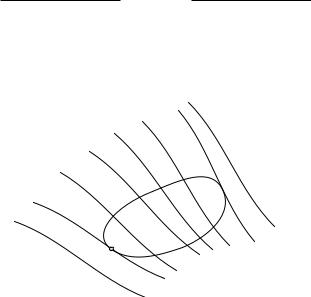
Рис. 186. Минимум разности P R − QR |
мает наибольшее или наимень- |
|||
шее значение, отрезки P R и QR |
||||
|
|
|||
образуют одинаковые углы с самой кривой C. Но нужно вместе с тем |
||||
отметить, что между случаем, когда C — прямая, и случаем, когда C — |
||||
замкнутая кривая, есть существенное различие: в первом случае при- |
||||
ходится разыскивать максимум абсолютной величины разности, т. е. |
||||
максимум |p − q|, тогда как во втором сама разность p − q достигает |
||||
инаибольшего и наименьшего значений.
§2. Общий принцип, которому подчинены экстремальные задачи
1.Принцип. Предыдущие задачи являются частными случаями некоторой общей проблемы, которую удобнее всего сформулировать аналитически. Возвращаясь к первой из рассмотренных задач, касающейся суммы p + q, мы видим, что она заключается в том, чтобы, обозначив через x, y координаты точки R, через x1, y1, координаты точки P и через
§ 2 |
ОБЩИЙ ЭКСТРЕМАЛЬНЫЙ ПРИНЦИП |
367 |
x2, y2 координаты точки Q, найти экстремальные значения функции
f(x, y) = p + q,
где положено
p p
p = (x − x1)2 + (y − y1)2, q = (x − x2)2 + (y − y2)2.
Рассматриваемая функция непрерывна во всей плоскости, но точка R с координатами x, y подчинена требованию находиться на кривой C. Эта последняя кривая, допустим, определена уравнением g(x, y) = 0; например, уравнением x2 + y2 − 1 = 0, если C — единичная окружность.
f (x, y)
R2
R1
Рис. 187. Экстремумы функции на кривой
Обратимся теперь к общей задаче: найти экстремальные значения некоторой данной функции f(x, y), если переменные x и y подчинены условию g(x, y) = 0. Постараемся охарактеризовать решение этой задачи. Для этого рассмотрим семейство кривых f(x, y) = c; при этом под «семейством» кривых понимаем совокупность всех кривых, определяемых указанным уравнением при различных значениях постоянной c (но такое значение неизменно для всех точек каждой кривой в отдельности). Предположим, что через каждую точку плоскости — или по крайней мере некоторой ее части, содержащей кривую C, — проходит одна и только одна кривая семейства f(x, y) = c. Тогда при непрерывном увеличении c кривая f(x, y) = c «заметает» некоторую часть плоскости, однако при этом ни одну точку не «заметает» дважды. (Примеры такого рода семейств: x2 + y2 = c, x + y = c, x = c.) В частности, одна кривая рассматриваемого семейства пройдет через точку R1, в которой f(x, y) принимает наибольшее значение на кривой C, и другая — через точку R2, в которой f(x, y) принимает наименьшее значение на C. Пусть наибольшее значение есть a, наименьшее — b. По одну сторону кривой f(x, y) = a значение f(x, y) = a меньше, чем a, по другую — больше, чем a. Так как
368 |
МАКСИМУМЫ И МИНИМУМЫ |
гл. VII |
на кривой C имеет место неравенство f(x, y) 6 a, то кривая C должна целиком лежать по одну и ту же сторону кривой f(x, y) = a; отсюда следует, что она в точке R1 касается кривой f(x, y) = a. Точно так же кривая C касается в точке R2 кривой f(x, y) = b.
Итак, доказана общая теорема: если в точке R на кривой C функция f(x, y) имеет экстремальное значение a, то кривая f(x, y) = a в точке R касается кривой C.
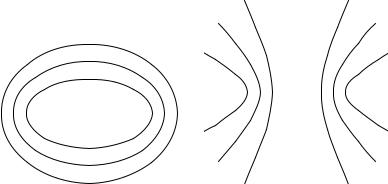
2. Примеры. Легко понять, что ранее полученные результаты являются частным случаем этой общей теоремы. Если речь идет об экстремуме суммы p + q, то функция f(x, y) есть p + q, а кривые f(x, y) = c — софокусные эллипсы с фокусами P и Q. В согласии с общей теоремой эллипсы, проходящие через те точки кривой C, где достигается экстремум одного или другого вида, касаются кривой C в этих точках. Если речь идет об экстремуме разности p − q, то функция f(x, y) есть p − q, и тогда кривые f(x, y) = c — софокусные гиперболы с фокусами P и Q; и в этом случае гиперболы, проходящие через точки, где достигается экстремум, касаются кривой C.
Рис. 188. Софокусные эллипсы Рис. 189. Софокусные гиперболы
Вот еще пример задачи того же типа. Дан отрезок прямой P Q и прямая l, его не пересекающая; требуется установить: из какой точки l отрезок P Q виден под наибольшим углом?
Функция, максимум которой надлежит определить в этой задаче, есть угол j, под которым из точки, движущейся по прямой l, виден отрезок P Q; если R — какая угодно точка плоскости с координатами x, y, то угол, под которым отрезок P Q виден из R, есть функция j = f(x, y) от переменных x, y. Из элементарной геометрии известно, что семейство кривых j = f(x, y) = const состоит из окружностей, проходящих через P и Q, так как хорда круга видна под одним и тем же углом из всех точек дуги окружности, расположенной по одну сторону хорды. Из рис. 190