ная Французской революцией, подготовила большое число офицеров, оказавших на военной службе выдающиеся услуги своей республике. В числе ее питомцев был Жан-Виктор Понселе (1788–1867), написавший свой «Трактат о проективных свойствах фигур» в 1813 г., будучи в плену

вРоссии.

ВXIX в. под влиянием Штейнера, Штаудта, Шаля и других проективная геометрия стала одним из излюбленных предметов математических исследований. Своей популярностью она обязана отчасти присущей ей особенной эстетической привлекательности, отчасти же способности проливать свет на геометрическую науку в целом, а также глубокой внутренней связи с неевклидовой геометрией и с алгеброй.

§2. Основные понятия

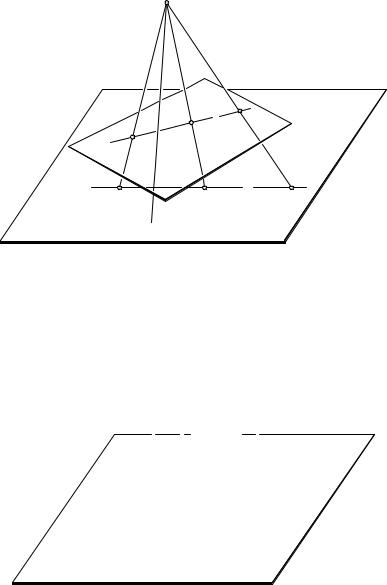
1.Группа проективных преобразований. Прежде всего определим класс, или «группу»1, проективных преобразований. Пусть в пространстве заданы две плоскости p и p0, параллельные или непараллельные между собой. Мы выполняем центральную проекцию p на p0 с данным центром O, не лежащим ни на p, ни на p0, сопоставляя каждой

точке P плоскости p такую точку P 0 плоскости p0, что P и P 0 лежат на одной и той же прямой, проходящей через O. Аналогично мы выполняем подобным же образом параллельную проекцию, предполагая, что проектирующие прямые параллельны между собой. Точно так же определяется проекция прямой или кривой линии l в плоскости p на некоторую линию l0 в плоскости p0, причем и в этом случае проекция может быть центральной или параллельной.

Всякое отображение одной фигуры на другую, получающееся посредством проектирования (центрального или параллельного) или же посредством конечной последовательности таких проектирований, называется проективным преобразованием2. Проективная геометрия плоскости или прямой составляется из системы геометрических теорем, сохраня-

1Термин «группа» в применении к классу преобразований подразумевает, что последовательное выполнение двух преобразований из рассматриваемого класса есть также преобразование этого класса и что преобразование, «обратное» по отношению к преобразованию из рассматриваемого класса, также принадлежит этому классу. Групповые свойства математических операций играли и продолжают играть очень большую роль во многих областях, однако по отношению к геометрии значение понятия «группы» в свое время, возможно, было несколько преувеличено.

2Если две фигуры связаны только одним проектированием, то говорят обычно,

что они перспективны. Таким образом, если сказано, что фигура F в результате проективного преобразования переходит в фигуру F 0, то это значит, что или фигуры F и F 0 перспективны, или же можно указать последовательность таких фигур F , F1, F2, . . . , Fn, F 0, что любые две рядом стоящие в ней фигуры перспективны.

ющихся при произвольных проективных преобразованиях соответствующих фигур. Проективной геометрии противопоставляется метрическая геометрия, которая понимается как система теорем, устанавливающих связи между величинами в рассматриваемых фигурах, инвариантные только относительно класса движений.

Некоторые проективные свойства можно формулировать непосредственно. Точка, разумеется, проектируется в точку. Далее, прямая линия проектируется в прямую: в самом деле, если прямая l в плоскости p проектируется на плоскость p0, то линия пересечения l0 плоскости p с плоскостью, проходящей через O и l, — обязательно прямая1. Если точка A и прямая l инцидентны2, то точка A0 и прямая l0, возникающие из них при проективном преобразовании, также инцидентны. Другими словами, инцидентность точки и прямой есть свойство, инвариантное относительно группы проективных преобразований. Из этого обстоятельства вытекает ряд простых, но весьма важных следствий. Если три точки (или более трех точек) коллинеарны, т. е. инцидентны с одной и той же прямой, то их отображения также коллинеарны. Аналогично, если в плоскости p три прямые (или более трех прямых) конкуррентны, т. е. инцидентны с одной и той же точкой, то их отображения — также конкуррентные прямые. В то время как эти простые свойства — инцидентность, коллинеарность, конкуррентность — являются проективными свойствами (т. е. свойствами, инвариантными относительно проективных преобразований), величины отрезков и углов, а также и отношения этих величин, вообще говоря, изменяются при проектировании. Равнобедренные или равносторонние треугольники могут, например, спроектироваться на треугольники с тремя различными сторонами. Отсюда следует, что хотя понятие «треугольник» принадлежит проективной геометрии, понятие «равносторонний треугольник» ей не принадлежит, а принадлежит только метрической геометрии.

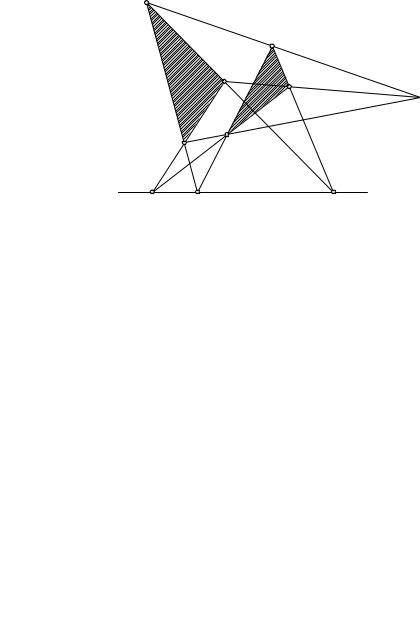
2. Теорема Дезарга. Одним из самых ранних открытий в области проективной геометрии является замечательная теорема Дезарга (1593– 1662): если на плоскости два треугольника ABC и A0B0C0 расположены таким образом, что прямые, соединяющие соответственные вершины, конкуррентны, то три точки, в которых пересекаются, будучи продолжены, три соответственные стороны, коллинеарны. Эта теорема здесь иллюстрируется чертежом (рис. 72), но пусть читатель проверит ее справедливость, экспериментируя на самостоятельно построенных

1За исключением того случая, когда прямая OP (или плоскость, проходящая через O и l) оказывается параллельной плоскости p. Такие исключения будут устранены в § 4.

2Точка и прямая называются инцидентными, если прямая проходит через точку или точка лежит на прямой. Этот «нейтральный» термин подчеркивает взаимность рассматриваемого отношения.

чертежах. Доказательство теоремы не является тривиальным, несмотря на всю простоту чертежа, состоящего только из прямых линий. Теорема явственно принадлежит проективной геометрии, так как при проектировании рассматриваемый чертеж не теряет свойств, упомянутых в теореме. В дальнейшем мы еще вернемся к этой теореме (стр. 207). В на-

C

O

Рис. 72. Конфигурация Дезарга на плоскости

стоящий же момент мы хотели бы привлечь внимание читателя к тому любопытному обстоятельству, что теорема Дезарга справедлива также и

втом предположении, что рассматриваемые треугольники расположены

вдвух различных (непараллельных) плоскостях и что подобного рода «трехмерная», или «пространственная» теорема Дезарга доказывается без малейших затруднений. По предположению, прямые AA0, BB0 и CC0 пересекаются в одной и той же точке O (рис. 73). В таком случае прямые AB и A0B0 лежат в одной плоскости и, значит, пересекаются в некоторой точке R; пусть, таким же образом, AC и A0C0 пересекаются в точке Q, а BC и B0C0 — в точке P . Так как точки P , Q и R находятся на продолжениях сторон треугольников ABC и A0B0C0, то все они лежат

вплоскости каждого из этих треугольников и потому — на прямой пересечения этих двух плоскостей. Значит P , Q и R коллинеарны, что и требовалось доказать.

Это простое доказательство наводит на мысль, что можно попытаться доказать «двумерную» теорему Дезарга, так сказать, с помощью перехода к пределу, постепенно сплющивая всю пространственную конструкцию таким образом, чтобы две плоскости в пределе совпали в одну, и в этой последней, вместе с другими, оказалась и точка O. Выполнить, однако, указанный предельный переход не так просто, так как прямая пересечения P QR при совмещении плоскостей не определяется