35 Http://joxi.Ru/19jGUhjKtjbaAdNjO7m

36Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции вокрестности некоторой точки.

Теорема:

Пусть функция имеет производную в некоторой окрестности точки ,  Пусть  Пусть  — произвольное положительное число, тогда: точка при или при :

Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).

Различные формы остаточного члена

В форме Лагранжа:

В форме Коши:

В интегральной форме:

37 http://nww13.narod.ru/vm1/5-2-3-3.html

38 Эйлера формулы

Эйлера формулы в математике, важнейшие формулы, установленные Л. Эйлером.

1) Э. ф., связывающие тригонометрические функции с показательной (1743):

e^ix = cos х + i sin х,

 , .

2) Э. ф., дающая разложение функции sin х в бесконечное произведение (1740):

 .

3) Тождество Эйлера о простых числах:

39 http://joxi.ru/-9rGUhjKTJBIAeZmUek

40Выпуклость функции

        Определение 7.5   Функция называется выпуклой вниз (или просто выпуклой) на интервале , если график функции идёт не выше хорды, соединяющей любые две точки графика и при .

Пусть . Тогда любую точку отрезка можно задать как , , а любую точку хорды -- как . Выражение задаёт линейную функцию переменного , график которой на отрезке совпадает с хордой.

То, что график функции идёт не выше хорды, означает, что

(7.4)

при всех .

Аналогично определяется выпуклость вверх: функция называется выпуклой вверх (или вогнутой) на интервале , если график функции идёт не ниже хорды, соединяющей любые две точки графика и при . Это означает, что

(7.5)

при всех .     

Рис.7.30.Графики выпуклой и вогнутой функций

Легко видеть, что функция вогнута на интервале в том и только том случае, когда функция выпукла на .

41 Введение в специальность – искать там

42 Интегрирование простейших дробей первого типа 

Для решения этой задачи идеально подходит метод непосредственного интегрирования: 

Интегрирование простейших дробей второго типа 

Для решения этой задачи также подходит метод непосредственного интегрирования:

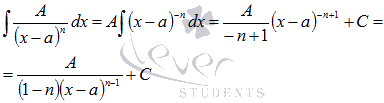
Интегрирование простейших дробей третьего типа 

Формула интегрирования простейших дробей третьего типа принимает вид: 

Интегрирование простейших дробей четвертого типа 

Первый шаг – подводим под знак дифференциала: 

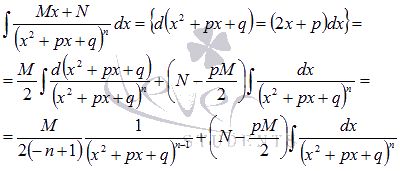
Второй шаг – нахождение интеграла вида . Интегралы подобного вида находятся с использованием рекуррентных формул. (Смотрите раздел интегрирование с использованием рекуррентных формул). Для нашего случая подходит следующая рекуррентная формула: 

43 http://joxi.ru/Tt3GUv3JTJCiESAqgrM

Необходимое условие интегрируемости функции на отрезке, виды интегрируемых функций.

Сформулируем необходимое условие существования определенного интеграла функции на отрезке.

Если функция y = f(x) интегрируема на отрезке [a; b], то она ограничена на нем.

Немного поясним. Это условие является необходимым, но не является достаточным. Что это значит? Если функция ограничена на отрезке, то не обязательно она интегрируема на нем. Но, если функция не ограничена на отрезке, тогда она не интегрируема на нем. Это условие используется для проверки возможности интегрирования функции на отрезке, то есть, проверяется ограниченность функции.

Перечислим виды функций, для которых существует определенный интеграл.

• Если функция непрерывна на отрезке [a; b], то она интегрируема на нем.

• Если функция ограничена на отрезке [a; b] и непрерывна во всех точках, кроме конечного их числа, то она интегрируема на [a; b]. На рисунке ниже приведен пример такой интегрируемой функции.

http://joxi.ru/st7GUv3JTJCvEVuUtHk