
Kretov1
.pdf
§ 4.1. еВЪУ‰ НУУр‰ЛМ‡Ъ М‡ ФОУТНУТЪЛ
617. Определить декартовы координаты точек, заданных
полярными координатами: |
|
|
а) М1(6; π/2), |
б) М2(5; 0), |
в) М3(2; π/4), |
г) М4(10; – π/3), |
д) М5(8; 2/3 π), |
е) М6(12; – π/6), |
ж) М7(2; π/6), |
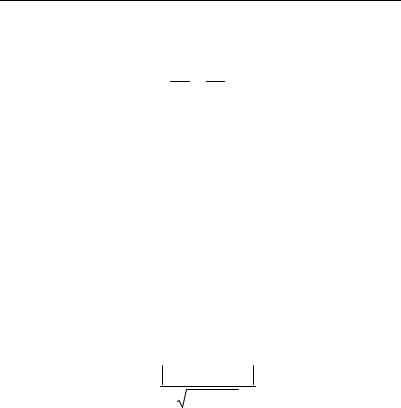
з) М8(√8; 3/4 π), |
и) М9(2; 11/6 π). |
618. Определить |
полярные координаты точек, заданных |
|
прямоугольными декартовыми координатами: |
||
а) М1(0; 5), |
б) М2(– 3; 0), |
в) М3(√3; 1), |
г) М4(– √2; –√2), |
д) М5(1; – √3), |
е) М6(0; – 3), |
ж) М7(1; – 1), |
з) М8(–3; 3), |
и) М9(2; 0). |
619. Определить полярные координаты точек, симметричных относительно полярной оси точкам:
а) М1(3; π/4), |
б) М2(2; π/2), |
в) М3(3; – π/3), |
г) М4(1; 2), |
д) М5(5; – 1). |
|
620. Определить полярные координаты точек, симметрич- |
||
ных относительно полюса точкам: |
|
|
а) М1(1; π/4), |
б) М2(5; π/2), |
в) М3(2; – π/3), |
г) М4(4; 5/6 π), |
д) М5(3; – 2). |
|
621. Вычислить полярные координаты середины отрезка,
соединяющего точки А и В: |
|
а) А(8; – 2/3 π), В(6; π/3); |
б) А(12; 4π/9), В(12; – 2/9 π). |
622.В полярной системе координат даны точки М1(ρ1; φ1)
иМ2(ρ2; φ2). Вычислить расстояние d между ними.
623.В полярной системе координат даны точки А и В, вычислить расстояние d между ними:
а) А(5; π/4), В(8; – π12), |
б) А(3; π/4), В(4; 3/4 π), |
в) А(2; π/12), В(1; 5/12 π), |
г) А(4; π/5), В(6; 6/5 π), |
д) А(3; 11/8 π), В(4; π/9 π). |
|
624. Вычислить площадь треугольника, одна из вершин которого помещается в полюсе, а две другие имеют полярные координаты (4; π/9) и (1; 5/18 π).
101

ЙО‡‚‡ IV. ДМ‡ОЛЪЛ˜ВТН‡fl „ВУПВЪрЛfl М‡ ФОУТНУТЪЛ
625. Вычислить площадь треугольника, заданного своими вершинами:
а) А(9; π/10), В(12; 4/15 π), С(10; 3/5 π), б) А(3; π/8), В(8; 7/24 π), С(6; 5/8 π).
626. Определить площадь квадрата, заданного двумя смежными вершинами:
а) М1(6; –7/12 π), М2(4; π/6), б) М1(12; –π/10), М2(3; π15).
§4.2. ирflП‡fl М‡ ФОУТНУТЪЛ
1.Уравнение прямой с угловым коэффициентом
y = kx + b, |
(4.2.1) |
где k = tg α (α — угол наклона прямой к оси Ох) называется угловым коэффициентом, b — начальная ордината.
Угол φ, отсчитанный против часовой стрелки от прямой y =k1x + b1 до прямой y = k2x + b2, определяется формулой:
tg φ = |
k2 −k1 |
. |
(4.2.2) |
|
|||
1+ k 1k2 |
|
||
Условие параллельности прямых: k1 = k2; |
|
||
Условие перпендикулярности прямых: k1 k2 = – 1 |
|
||
2. Общее уравнение прямой: |
|
||
Ах + Вy + С = 0, |
(4.2.3) |
||
где А и В одновременно не обращаются в нуль (А2 + В2 ≠ 0), А и В — координаты вектора, перпендикулярного прямой.
Частные случаи:
1)С = 0, Ах + Ву = 0 — прямая проходит через начало координат;
2)В = 0, А ≠ 0, С ≠ 0, Ах + С = 0 — прямая параллельна оси Оу;
3)В = 0, А ≠ 0, С = 0 — ось Оу;
4)А = 0, В ≠ 0, С ≠ 0, Ву + С = 0 — прямая параллельна оси Ох;
5)А = 0, В ≠ 0, С = 0 — ось Ох.
102
§ 4.2. ирflП‡fl М‡ ФОУТНУТЪЛ
Если две прямые заданы общими уравнениями
А1х + В1у + С1 = 0; А2х + В2у + С2 = 0, то условие их параллельности:
A1 = B1 ,
A2 B2
условие перпендикулярности: А1А2 + В1В2 = 0. 3. Уравнение прямой в отрезках:
|
x |
+ |
y |
=1. |
(4.2.4) |
|
a |
|
|||
|
|
b |
|
||
4. Нормальное уравнение прямой |
|
||||
x cosα + y sinα – ρ = 0, |
(4.2.5) |
||||
где ρ — длина перпендикуляра, опущенного из начала координат на прямую, α — угол наклона этого перпендикуляра к оси Ох.
Расстояние d от точки М(х0; у0) до прямой вычисляется по формуле:
d = |x0 cosα + y0 sinα – ρ| |
(4.2.6) |
или |
|
d = |
Ax0 + By0 +C |
, |
(4.2.7) |
|
A2 + B2 |
||||
|
|
|
||
если прямая задана общим уравнением. |
|
|
||
5. Уравнение прямой, проходящей |
через |
данную точку |
||
М(х0; у0) в данном направлении, имеет вид: |
|
|||
у – у0 = k(x – x0). |
|
(4.2.8) |
||
Уравнение прямой, проходящей через две точки М1(х1; у1),
М2(х2; у2):
y − y1 |
= |
x − x1 |
, |
(4.2.9) |
||||
|
|
|||||||
y |
2 |
− y |
|
x |
2 |
− x |
|
|
|
1 |
|
|
1 |
|
|
||
если х1 = х2, то уравнение прямой: х = х1, если у1 = у2, то уравнение прямой: у = у1.
103

ЙО‡‚‡ IV. ДМ‡ОЛЪЛ˜ВТН‡fl „ВУПВЪрЛfl М‡ ФОУТНУТЪЛ
бДСДзаь
627.Написать уравнение прямой, параллельной биссектрисе первого координатного угла и отсекающей на оси Оу отрезок, величина которого равна семи единицам.
628.Написать уравнение прямых, параллельных биссектрисе второго координатного угла и отсекающих на оси Оу отрезки:
а) b = 4; б) b = – 5; |
в) b = 3,5; г) b = – 2,7; д) b = 5. |
||
629. |
Найти уравнения прямых, отсекающих на оси Ох от- |
||
резок, равный 5, и образующих с осью Ох углы: |
|||
а) α = 45°; б) α = 30°; |
в) α = 60°; г) α = 135°; д) α = 180°. |
||
630. |
Привести к виду уравнений с угловыми коэффициен- |
||
тами уравнения следующих прямых: |
|
||
а) 5х – у + 3 = 0; |
б) 3х + 8у = 0; |
в) 4у – 7х = 0; |
|
г) 6х + 3у – 10 = 0; д) 2х – 5у + 15 = 0; е) 4х – 2у – 5 = 0. |
|||
631. |
Найти углы, образуемые с осью Ох прямыми: |
||
а) 2х + 2у – 5 = 0; б) 3х – 3у + 1 = 0; в) 4у + 7х = 0; |
|||
г) 2х + 9 = 0; |
д) 5х – 4у = 0; |
е) 4х – 5у + 6 = 0. |
|
632. |
Определить отрезки, отсекаемые на осях координат |
||
прямыми: |
|
|
|
а) 3х + 4у – 12 = 0; б) у = 6х + 1; в) 7х – 3у + 21 = 0; г) 4х – 5у – 20 = 0; д) у = 8 – 4х; е) 9х + 4у + 36 = 0.
633. |
При каком с прямая 3х + 5у + с = 0 отсекает на оси Оу |
||
отрезок: |
|
|
|
а) b = 2; б) b = – 3; |
в) b = 6; г) b = –0,2; д) b = 0,1. |
||
634. |
Найти значения В, при которых прямая 7х +Ву + 3 = 0 |
||
образует с осью Ох углы: |
|
|
|
|
а) φ = 45°; |
б) φ = 135°; |
в) φ = 60°; |
|
г) φ = 30°; |
д) φ = 120°; |
е) φ = 150°. |
635. |
Определить параметр b, при котором прямая у=5х+b |
||
отсекает на оси Ох отрезок: |
|
||
|
а) а = 4; б) а = – 3; в) а = 0,2; г) а = – 0,9. |
||
636. |
Составить уравнение прямой, отсекающей на оси ор- |
||
динат отрезок b = – 3 и образующей с осью Ох угол α = 30°.
104

§ 4.2. ирflП‡fl М‡ ФОУТНУТЪЛ
637.Составить общее уравнение прямой, отсекающей на осях координат отрезки а = 2/5; b = –0,1.
638.Определить площадь треугольника, образованного прямой 3х + 4у – 36 = 0 и осями координат.
639.Составить уравнение прямой, проходящей через начало координат и точку М(– 2; –3)
640.Составить уравнение прямой, проходящей через точку М(2; 5) и отсекающей на оси ординат отрезок b = 7.
641.Составить уравнения прямых, проходящих через точку М(– 3; – 4) и параллельных осям координат.
642.Через точку М(5; 2) провести прямую, отсекающую равные отрезки на осях координат.
643.Равнобедренная трапеция с основаниями 8 и 2 см имеет острый угол 45°. Написать уравнения сторон трапеции, приняв за ось Ох большее основание, а за ось Оу — ось симметрии трапеции.
644.Написать уравнения сторон ромба с диагоналями 10 и 6 см, приняв большую диагональ за ось Ох и меньшую — за ось Оу.
645.Найти углы между прямыми:
а) у=1/3х+4, у=2х–3; |
б) у=–1/5х+6, у=–3/2х+7; |
в) у=1/6х–10, х–6у+9=0; |
г) у=2/9х–1, 9х+2у–5=0; |
д) х + √3у – 2 = 0, 3х +√3у + 5 = 0; е) х – 3у + 4 = 0, 2х – у + 6 = 0; ж) 7х + 19у – 16 = 0, 5х – 4у – 12 = 0; з) 2х – 2у – 1 = 0, 6х – 2у + 5 = 0.
646. Указать, какие из следующих прямых параллельны и
перпендикулярны: |
|
а) 3х + 5у – 1 = 0; |
б) 6х + 10у – 3 = 0; |
в) 5х – 3у + 2 = 0; |
г) 6х – 10у + 7 = 0. |
647. Составить уравнение прямой, проходящей через точки |
|
М1 и М2: |
|
а) М1(–1; 3), М2(2; 5); |
б) М1(–2; 4), М2(–2; –1); |
в) М1(2; 2), М2(–4; –5); |
г) М1(8; 2), М2(0; 2); |
д) М1(0; 1), М2(6; 5); |
е) М1(1; 4), М2(6; –5). |
648. Вычислить площадь треугольника, стороны которого за-
даны уравнениями: 3х – 2у + 5 = 0; х + 3у + 9 = 0; 9х + 5у – 29 = 0.
105

ЙО‡‚‡ IV. ДМ‡ОЛЪЛ˜ВТН‡fl „ВУПВЪрЛfl М‡ ФОУТНУТЪЛ
649.Через точку М(2; –4) провести прямую, параллельную
иперпендикулярную прямой 3х + 5у – 6 = 0.
650.Данывершинытреугольника А(2; 2), В(–2; –8), С(–6; –2). Составить уравнения медиан треугольника.
651.Даны вершины треугольника А(0; 1), В(6; 5), С(12; –1). Составить уравнение высоты треугольника, проведенной из вершины С, и длину высоты.
652.Определитьрасстояниемеждупараллельнымипрямыми:
а) 3х + у – 3√10 = 0, 6х + 2у + 5√10 = 0; б) 6х + 8у – 35 = 0, 3х + 4у – 11 = 0; в) 3/5 х + 4/5 у – 2/5 = 0, 3х + 4у – 42 = 0; г) 12х + 5у – 13 = 0, 12х + 5у – 39 = 0.
653.Даны уравнения оснований трапеции: 4х + 3у – 20 = 0, 4х + 3у – 45 = 0. Вычислить длину ее высоты.
654.Вычислить площадь квадрата, две стороны которого лежат на прямых 8х + 6у + 10 = 0, 8х + 6у – 10 = 0.
655.Даны вершины треугольника А(1; 1), В(10; 13), С(13; 6). Составить уравнение биссектрисы угла А.
656.Составить уравнения прямых, проходящих через точку М(5; 1) и образующих с прямой 2х + у – 4 = 0 угол 45°.
657.Даны стороны треугольника х + у – 6 = 0, 3х – 5у + 14 = 0
и5х – 3у – 14 = 0. Составить уравнения высот треугольника.
658.Составить уравнения биссектрисы углов между пря-
мыми 3х + 4у – 20 = 0 и 8х + 6у – 5 = 0.
659.ДанывершинытреугольникаА(0; 0), В(–1; –3), С(–5; –1). Составить уравнения прямых, проходящих через вершины треугольника и параллельных сторонам треугольника.
660.Составить уравнения прямых, проходящих через точ-
ку М(2; 7) и образующих с прямой, проходящей через точки А(– 1; 7) и В(8; – 2) углы по 45°.
661.Определить расстояние от точки М(2; – 1) до прямой, отсекающей на осях координат отрезки а = 8, b = 6.
662.При каком значении m прямые 7х – 2у – 5=0, х+7у–8=0
иmx + my –8 = 0 пересекаются в одной точке.
106

§ 4.2. ирflП‡fl М‡ ФОУТНУТЪЛ
663.Точки А(1; 2) и С(3; 6) являются противоположными вершинами квадрата. Определить координаты двух других вершин.
664.На оси абсцисс найти точку, расстояние которой от прямой 8х + 15у + 10 = 0 равно 1.
665.Найти прямую, проходящую через точку пересечения прямых:
а) х + 6у + 5 = 0, 3х – 2у + 1 = 0 и через точку М(–4/5; 1);
б) х + 2у + 3 = 0, 2х + 3у + 4 = 0 и параллельную прямой
5х + 8у = 0;
в) 3х – у – 1 = 0, х + 3у + 1 = 0 и параллельную оси Ох; г) х + 2у + 1 = 0, 2х + у + 2 = 0 и образующую угол 135° с
осью абсцисс.
§ 4.3. äðË‚˚ ‚ÚÓðÓ„Ó ÔÓðfl‰Í‡
Определение 1. Линии, определяемые алгебраическими уравнениями второй степени относительно переменных x и y, то есть уравнениями вида
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0,
(A2 + B2 + C2 ≠ 0) |
(4.3.1) |
называются кривыми второго порядка.
Определение 2. Окружностью называется множество всех точек плоскости, удаленных от заданной точки А на одно и то же расстояние R. Точка А называется центром, а R — радиусом окружности.
В прямоугольной системе координат уравнение окружности имеет вид:
(x – a)2 + (y – b)2 = R2, |
(4.3.2) |
где (a; b) — координаты ее центра. Уравнение (4.3.2) называется каноническим уравнением окружности.
Определение 3. Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
107

ЙО‡‚‡ IV. ДМ‡ОЛЪЛ˜ВТН‡fl „ВУПВЪрЛfl М‡ ФОУТНУТЪЛ
Каноническое уравнение эллипса:
x2 |
+ |
y2 |
=1, |
(4.3.3) |
|
a2 |
b2 |
||||
|
|
|
где a — большая полуось, b — малая полуось эллипса. Координаты фокусов: F1(– c; 0), F2(c; 0), где c — половина
расстояния между фокусами (рис. 4.1). Числа a, b и c связаны соотношением
c2 = a2 – b2. |
(4.3.4) |
Рис. 4.1
Точки A, B, C, D называются вершинами эллипса, точка О — центром эллипса, расстояния r1 и r2 от произвольной точки М эллипса до его фокусов называются фокальными радиусами этой точки.
Определение 4. Эксцентриситетом ε эллипса называется отношение фокусного расстояния 2с к большой оси 2а:
ε = |
c |
(ε < 1). |
(4.3.5) |
|
|||
|
a |
|
|
Фокальные радиусы определяются формулами: |
|
||
r1 = a + εx, r2 = a – εx, (r1 + r2 = 2a). |
(4.3.6) |
||
Определение 5. Директрисами эллипса называются прямые l1 и l2, параллельные малой оси эллипса и отстоящие от нее на расстоянии, равном а/ε.
108

§ 4.3. äðË‚˚ ‚ÚÓðÓ„Ó ÔÓðfl‰Í‡
Уравнения директрис: |
|
|
|
|
|
x = |
a |
и x = – |
a |
. |
(4.3.7) |
ε |
|
||||
|
|
ε |
|
||
Замечание 1. Если a = b, то уравнение (4.4.3) определяет окружность x2 + y2 = a2.
Замечание 2. |
Если фокусы эллипса лежат на оси Oy, то |
|||||||||
|
|
b > a, c2 = b2 – a2, |
(4.3.8) |
|||||||
|
|
|
ε = |
c |
, |
|
(4.3.9) |
|||
|
|
|
||||||||
|
|
|
|
|
|
|
b |
|
||
уравнения директрисы y = ± |
b |
. |
|
|
|
|
||||
|
|
|
|
|
|
|||||
|
|
|
|
ε |
|
|
|
|
||
Замечание 3. |
Уравнение эллипса с осями, параллель- |
|||||||||
ными координатным, имеет вид |
|
|
|
|
||||||
|
(x − x0 )2 |
+ |
(y − y0 )2 |
=1, |
(4.3.10) |
|||||
|
|
|
||||||||
|
|
a2 |
|
b2 |
|
|||||
где (x0; y0) — координаты центра эллипса. |
|
|||||||||
Замечание 4. |
Уравнения |
|
|
|
|
|||||
|
|
x = accost, |
|
|||||||
|
|
y = b sin t, t [0; 2π] |
(4.3.11) |
|||||||
являются параметрическими уравнениями эллипса (t — величина угла между осью Ox и прямой OM, соединяющей центр эллипса О с его точкой М).
Определение 6. Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы
x2 |
− |
y2 |
=1, |
(4.3.12) |
|
a2 |
b2 |
||||
|
|
|
где a — действительная, b — мнимая полуось гиперболы.
109

ЙО‡‚‡ IV. ДМ‡ОЛЪЛ˜ВТН‡fl „ВУПВЪрЛfl М‡ ФОУТНУТЪЛ
Числа 2a и 2b называются соответственно действительной и мнимой осями гиперболы. Координаты фокусов F1(– c; 0), F2(c; 0), c — половина расстояния между фокусами (рис. 4.2).
Рис. 4.2 |
|
Числа a, b и c связаны соотношением: |
|
c2 = a2 + b2. |
(4.3.13) |
Точки A и B называются вершинами гиперболы, точка О — центром гиперболы, расстояния r1 и r2 от произвольной точки М гиперболы до ее фокусов называются фокальными радиусами этой точки.
Определение 7. Число
ε = |
c |
(ε > 1) |
(4.3.14) |
|
|||
|
a |
|
|
называется эксцентриситетом гиперболы. |
|
||
Фокальные радиусы определяются формулами: |
|
||
для точек правой ветви гиперболы: |
|
||
r1 = a + εx, r2 = – a + εx; |
(4.3.15) |
||
для точек левой ветви: |
|
||
r1 = – a – εx, r2 = a – εx. |
(4.3.16) |
||
Определение 8. Прямоугольник, центр которого совпадает с точкой О, а стороны равны и параллельны осям гиперболы, называется основным прямоугольником гиперболы.
110
