3.6. Доминирование стратегий

Принципы доминирования, изложенные в данном параграфе, позволяют упростить игровую задачу посредством ее сведения к задаче меньшей размерности.

Определение 6. Чистая стратегия игрокаP1 доминирует чистую стратегию (соответственно чистая стратегияигрокаP2 доминирует чистую стратегию ), если для всех() выполняются неравенства:

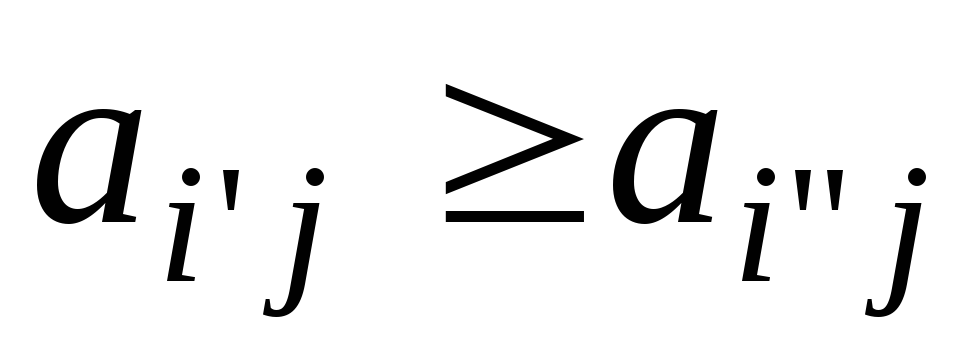( соответственно ).

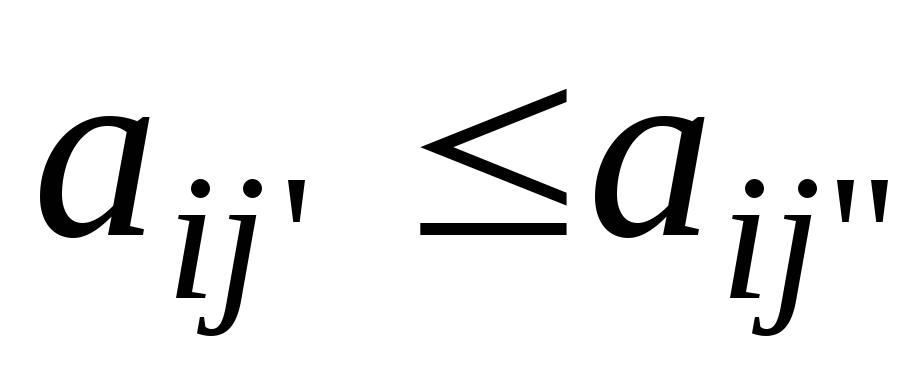Аналогичное определение можно ввести для смешанных стратегий.

Определение 7. Смешанная стратегия игрокаP1 доминирует (строго доминирует) смешанную стратегию в игре, если для всех чистых стратегийигрокаP2 выполнены неравенства:

,

().

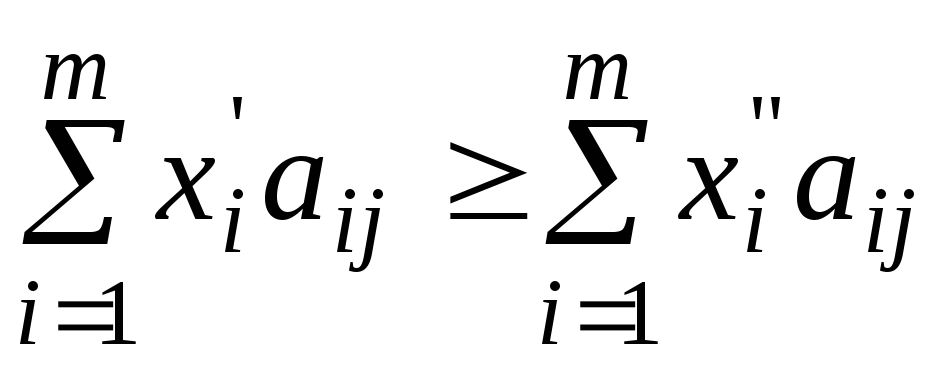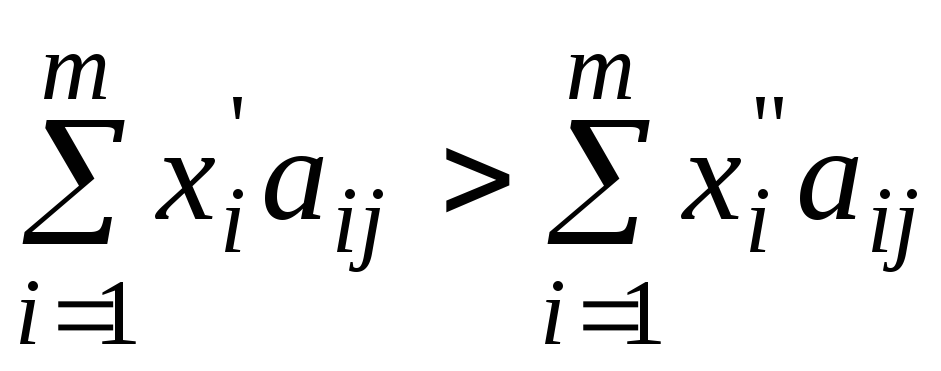Определение 7 означает, что выбор первым игроком стратегии для любой чистой стратегии второго игрокаj дает не меньшее математическое ожидание выигрыша P1, чем использование стратегии .

Аналогично вводится понятие доминирования для смешанных стратегий игрока P2.

Определение 8. Смешанная стратегия игрокаP1 доминирует (строго доминирует) смешанную стратегиюв игре, если для всех чистых стратегийигрокаP1 выполнены неравенства:

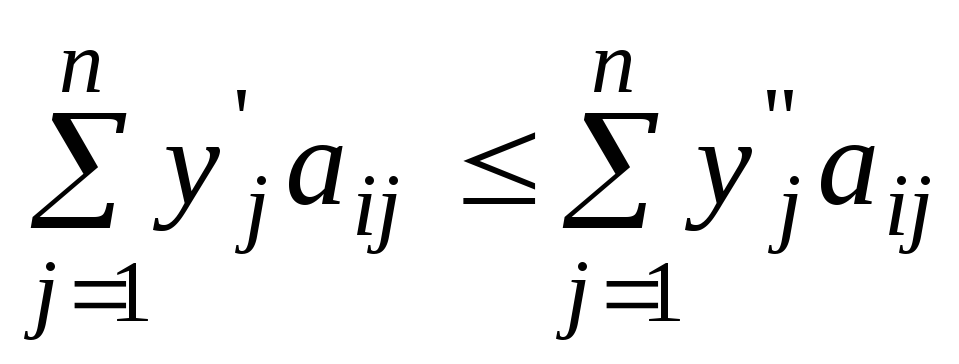(то есть ,),

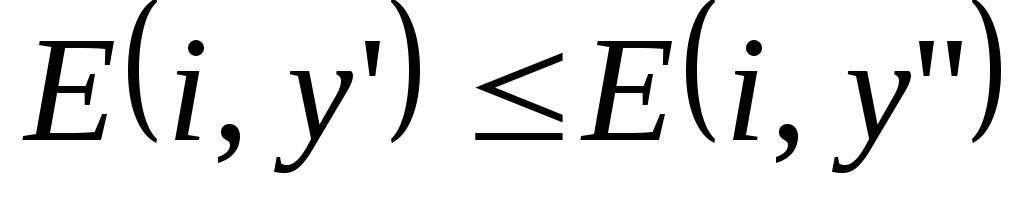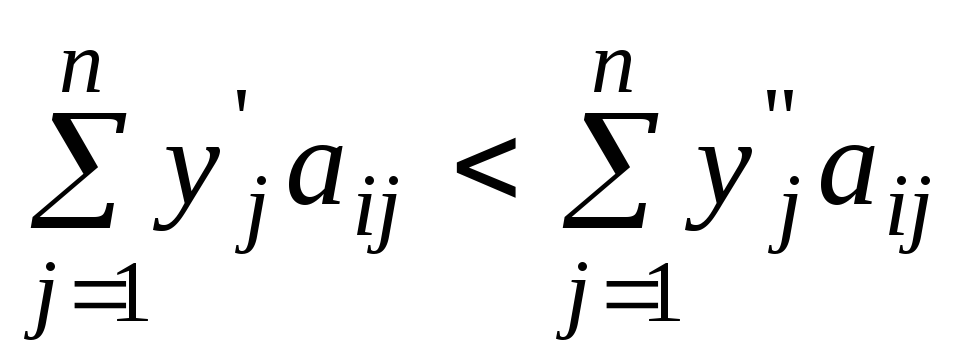(, то есть,).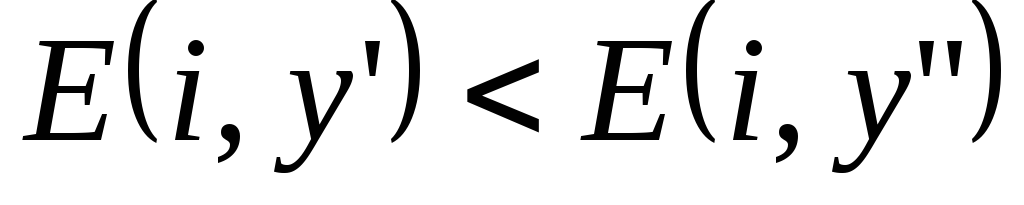

Определение 9. Стратегия () игрокаP1 (P2) называется (строго) доминируемой, если существует стратегия () игрокаP1 (P2), которая (строго) доминирует ().

В противном случае стратегия называется недоминируемой (соответственно строго недоминируемой).

Справедливы следующие теоремы.

Теорема 3. Если в игре стратегияигрокаP1 доминирует оптимальную стратегию тотакже оптимальна.

Теорема 4. Если в игре стратегияодного из игроков оптимальна, то– недоминируемая строго стратегия.

Замечание 3. Обратное утверждение теоремы 4 не всегда верно. Так, например, в игре с матрицей первая и вторая чистые стратегии Р1 недоминируемые, но не являются оптимальными.

Введенные ниже определение и теорема являются основополагающим моментом решения задачи упрощения матрицы антагонистической игры.

Определение 10. Рассмотрим смешанную стратегию первого игрока и число. Векторназываетсярасширением стратегии наi-ом месте.

Так, например, расширением стратегии на втором месте будет являться вектор, а расширением на четвертом месте – вектор.

Теорема 5. Пусть – антагонистическая игра. Предположим, что строкаi матрицы A доминируема (то есть доминируема i-ая чистая стратегия P1) и пусть – игра с матрицей, получаемой изA вычеркиванием i-ой строки.

Тогда:

1) ;

2) всякая оптимальная стратегия игрокаP2 в игре является оптимальной и в игре;

3. если 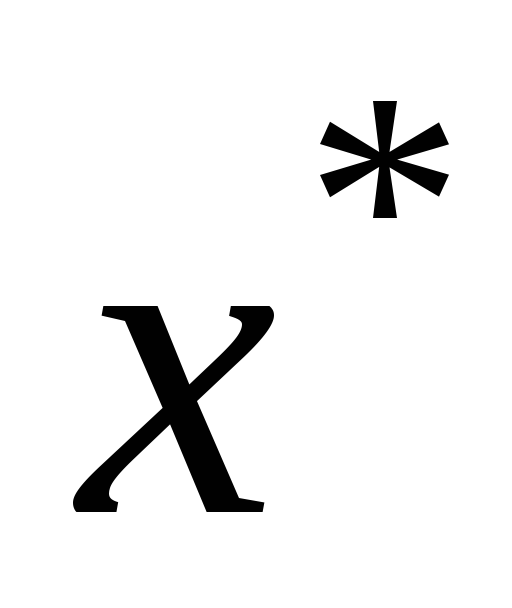– произвольная оптимальная стратегия игрока Р1 в игре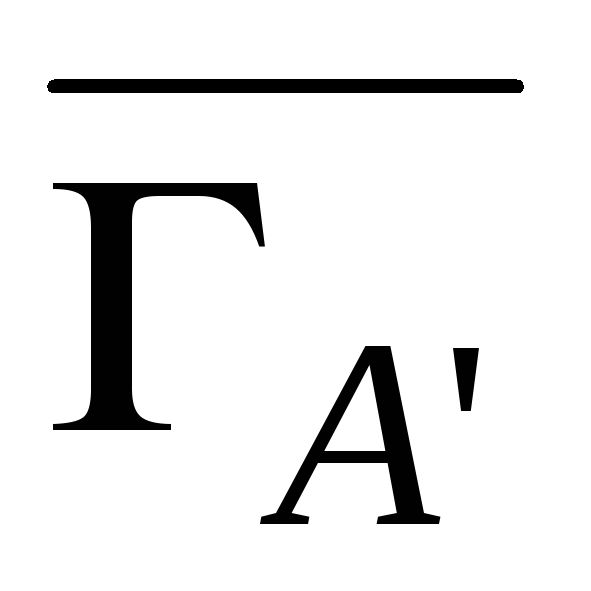и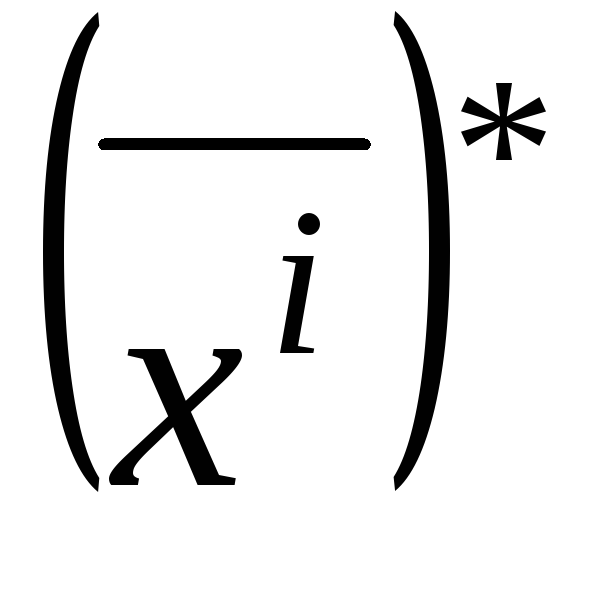– расширение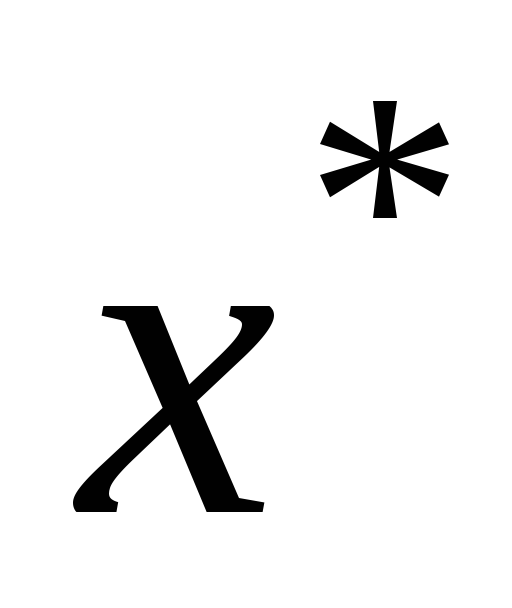наi-ом месте, то 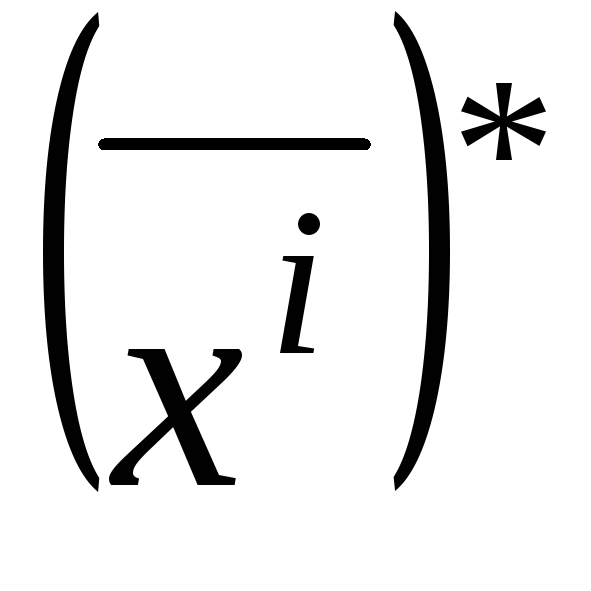оптимальна для Р1 в игре;

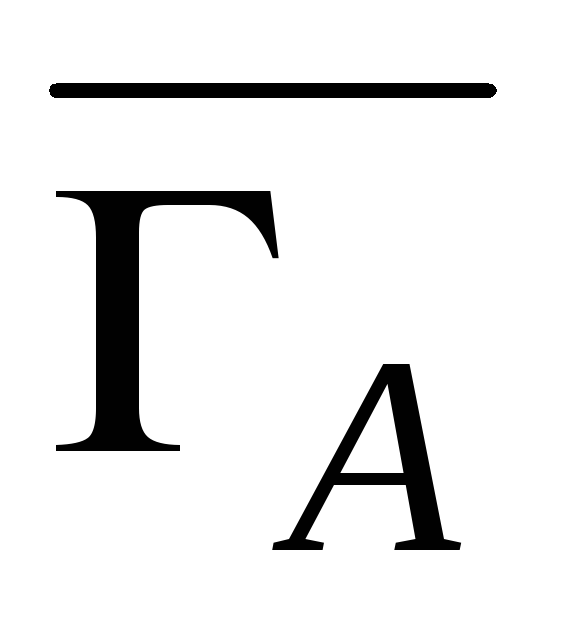4. если i–я строка матрицы A строго доминируема, то произвольная оптимальная стратегия 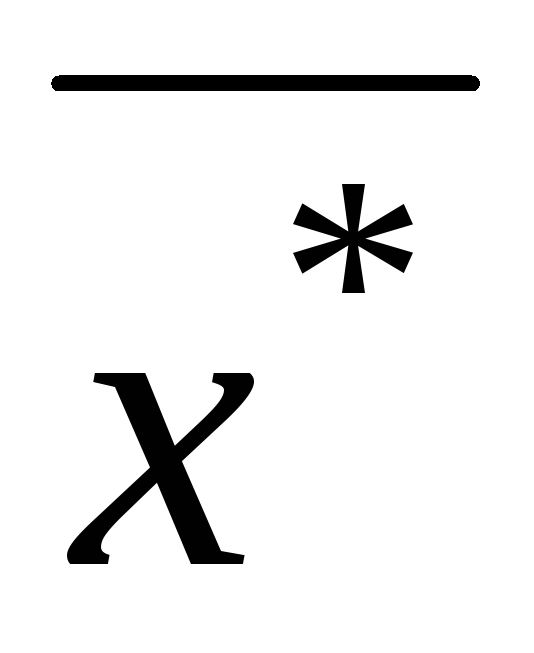игрока Р1 в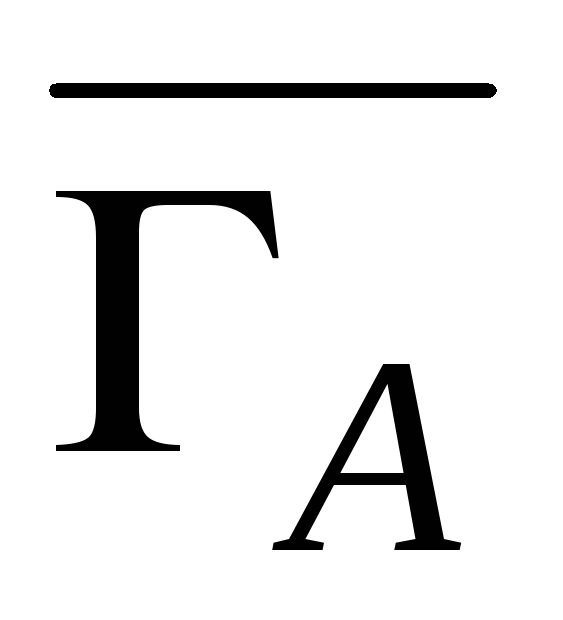может быть получена из некоторой оптимальной стратегии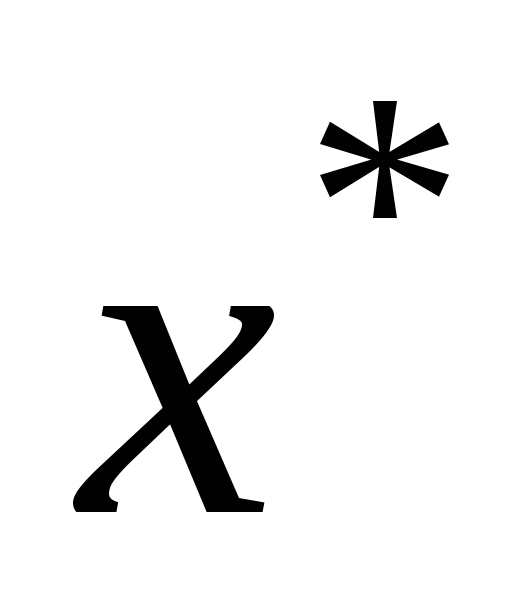в игре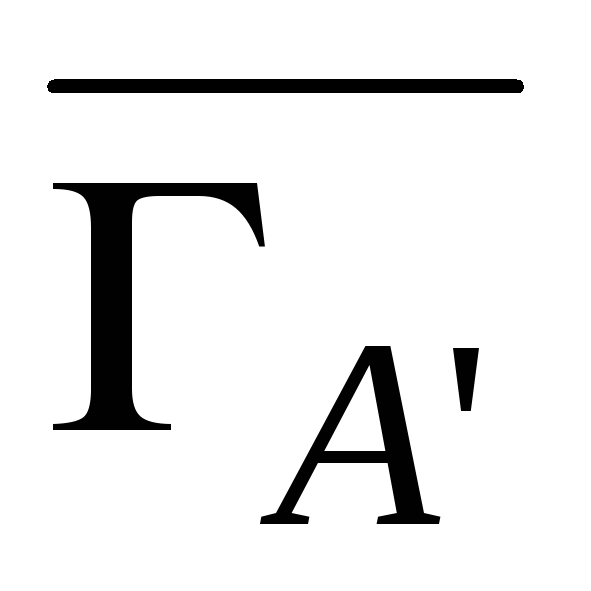расширением наi-ом месте.

Для практического решения задач полезно доказать следующую лемму.

Лемма 4. Если смешанная стратегия в игредоминируетi-ую чистую стратегию игрока Р1, то существует смешанная стратегия , доминирующаяi–ую чистую стратегию.

Доказательство

Предположим для определенности, что строка m матрицы A доминируема стратегией . Если, то построим стратегию, доминирующую стратегиюm.

Положим .

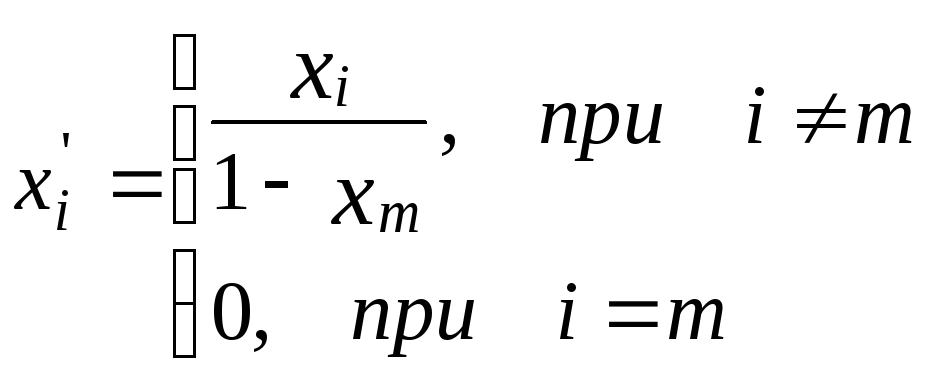Покажем, что – смешанная стратегия.

При этом , так как. Кроме того,. Следовательно,.

Покажем, что доминирует чистую стратегиюm.

Так как x доминирует m, то .

Тогда ;

;

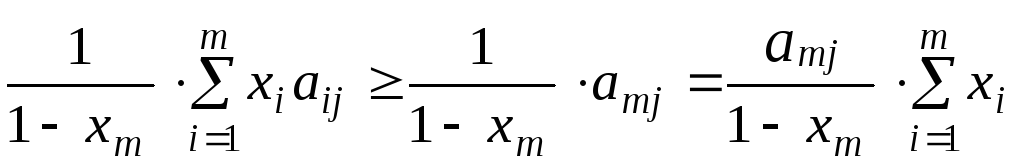, а так как , то, что означает доминирование стратегии.