
- •И.Н.Булгакова, ю.В.Бондаренко, г.Д.Чернышова
- •§ 1. Основные понятия исследования операций. Математическая модель операции
- •§ 2. Понятие игры. Классификация игр
- •§ 3. Антагонистические игры в нормальной форме
- •3.1 Определение антагонистической игры в нормальной форме. Матричные игры
- •Примеры
- •3.2 Ситуация равновесия в чистых стратегиях: понятие и существование
- •Упражнения к § 3.1. – 3.2
- •3.3 Смешанное расширение игры
- •3.4 Методы решения матричных игр
- •3. Сведение игры к задаче линейного программирования
- •3.5 Существование оптимальных стратегий. Теорема фон Неймана-Нэша
- •Упражнения к § 3.3–3.5
- •3.6. Доминирование стратегий
- •Примеры
- •Упражнения к § 3.6
- •3.7 Игры с частными случаями платежных матриц
- •§ 4. Игры в условиях неопределенности и риска (игры с природой)
- •Принятие решений в условиях полной неопределенности
- •Принятие решений в условиях риска
- •Примеры
- •Упражнения к § 4
- •§ 5 Позиционые игры
- •Упражнения
- •Список литературы
- •I. Основная литература
- •II. Дополнительная литература
3. Сведение игры к задаче линейного программирования
Пусть
![]() – матрица антагонистической игры с
элементами
– матрица антагонистической игры с
элементами![]() (это условие обеспечивает положительность
цены игрыv).
(это условие обеспечивает положительность
цены игрыv).
Пусть
![]() – смешанная стратегия первого игрока,
– смешанная стратегия первого игрока,![]() – смешанная стратегия второго игрока.
Тогда из неравенств свойства 2 оптимальных
стратегий смешанного расширения игры
получаем:
– смешанная стратегия второго игрока.
Тогда из неравенств свойства 2 оптимальных
стратегий смешанного расширения игры
получаем:
![]() ,
,
![]() ,
,
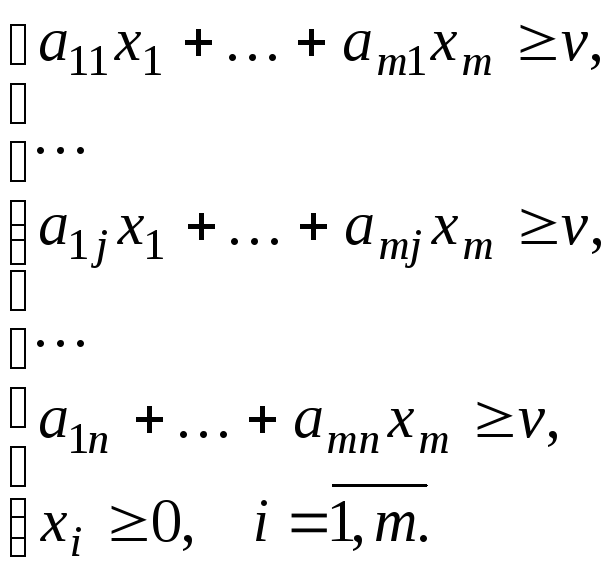
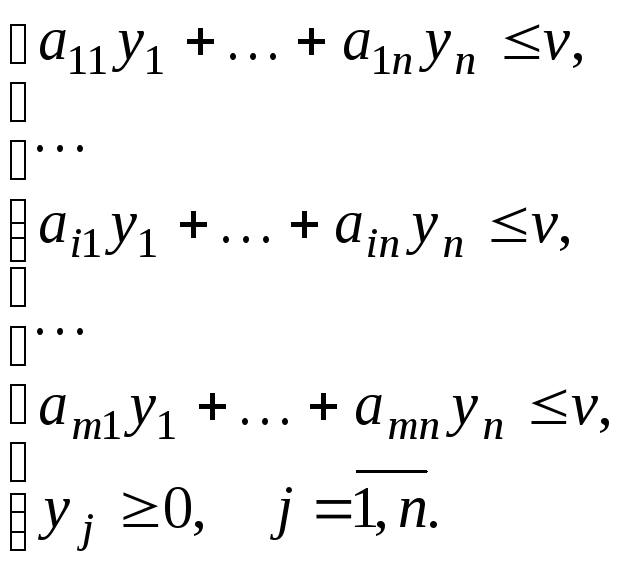
Разделим уравнения и неравенства систем на v>0:
 ,
,
![]() ,
,
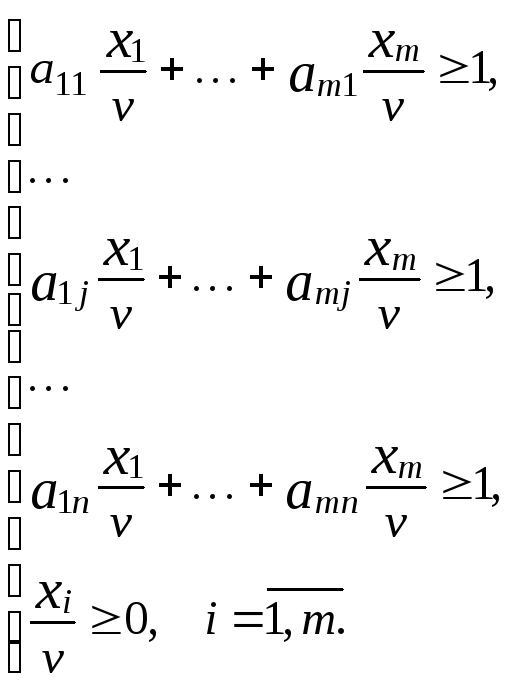
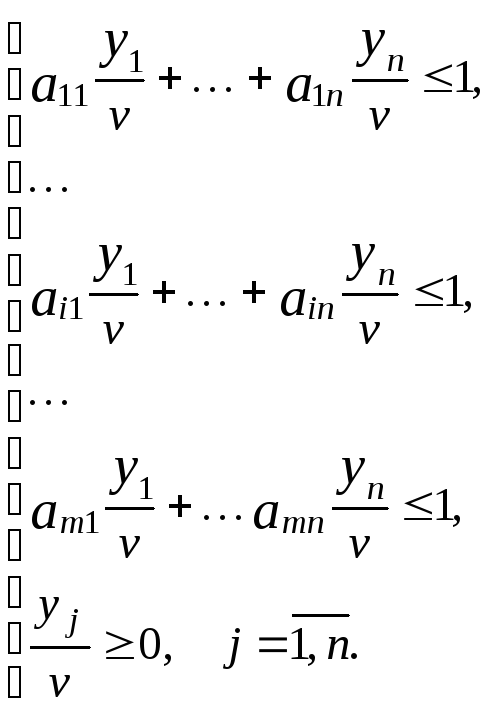
Введем
замену:
![]() ,
,![]() ,
,![]() ;
;![]() .
Тогда:
.
Тогда:
![]() ,
,
![]() ,
,
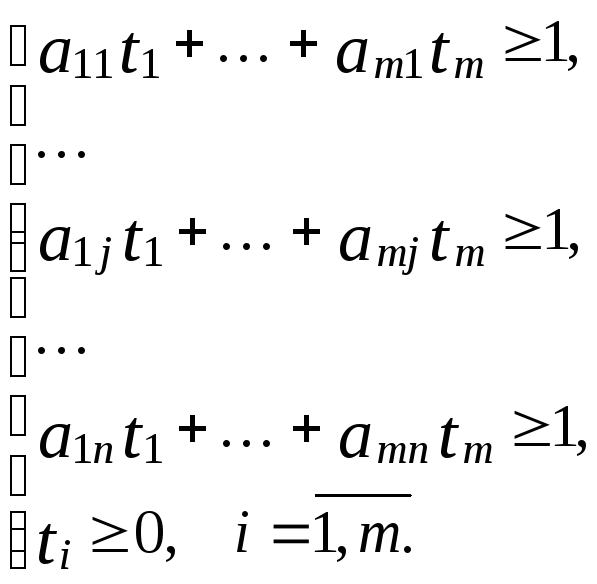
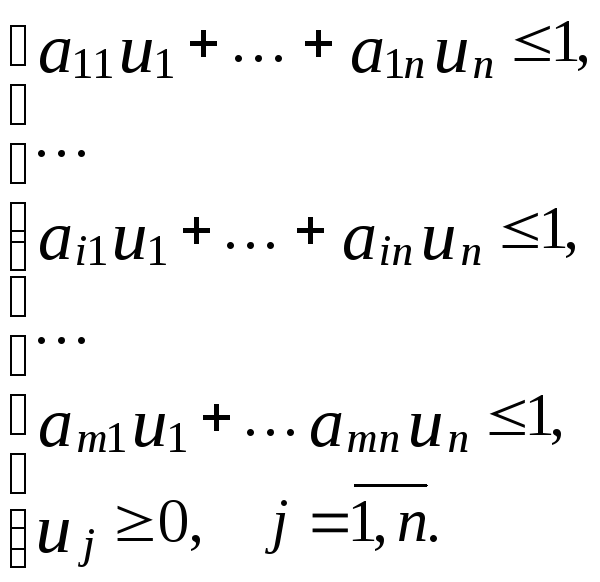
Так
как первый игрок максимизирует величину
гарантированного выигрыша (v)
и, соответственно, минимизирует величину
![]() ,
а второй игрок максимизирует величину
,
а второй игрок максимизирует величину![]() ,
то получаем следующие двойственные
друг другу задачи линейного программирования:
,
то получаем следующие двойственные
друг другу задачи линейного программирования:
![]() ,
,
![]() ,
,
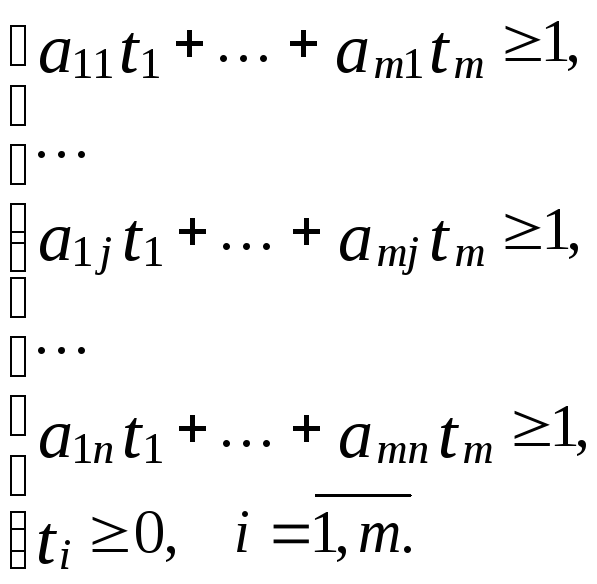 (4)
(4)
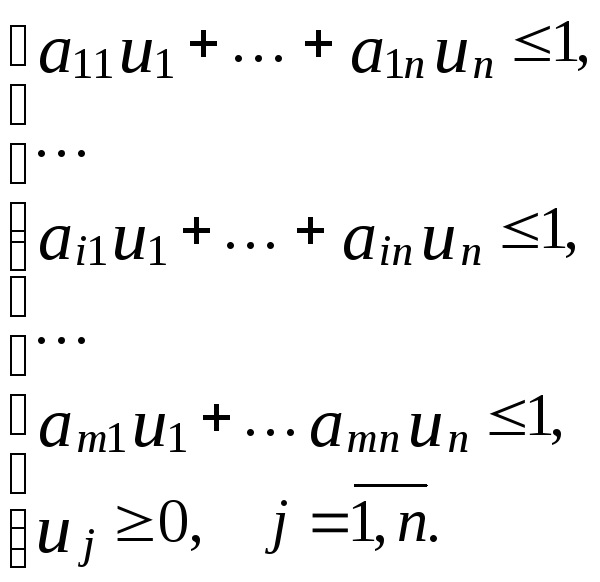 (4д)
(4д)
В
теореме фон Неймана-Нэша п. 2.5 будет
доказано, что если
![]() – решения задачи (4) и (4д) соответственно,
то
– решения задачи (4) и (4д) соответственно,
то![]() – цена игры, а координаты оптимальных
стратегий вычисляются по формулам:
– цена игры, а координаты оптимальных
стратегий вычисляются по формулам:
![]()
![]() ;
;
![]()
![]() .
.
При
этом, так как решения прямой и двойственной
задачи связаны соотношением:
![]() ,
где
,
где
![]() является матрицей обратной к оптимальной
базисной матрице, то для нахождения
ситуации равновесия достаточно решить
одну из задач (4) или (4д).
является матрицей обратной к оптимальной
базисной матрице, то для нахождения
ситуации равновесия достаточно решить
одну из задач (4) или (4д).
Если
матрица игры имеет произвольный вид,
то по лемме о масштабе всегда существует
матрица
![]() ,
где
,
где![]() такая, что элементы матрицы
такая, что элементы матрицы![]() положительны. В этом случае решается
задача с новой матрицей В, а решения
исходной задачи совпадают с ее решением.
положительны. В этом случае решается
задача с новой матрицей В, а решения
исходной задачи совпадают с ее решением.
Примеры
Пример 4. Решить матричную игру методом сведения к задаче линейного программирования, если матрица игры имеет вид:
 .
.
Решение
Так
как матрица игры содержит неположительные
элементы, то рассмотрим матрицу
![]() ,
где
,
где![]() ,
,![]() ,
,![]() .
Тогда матрица
.
Тогда матрица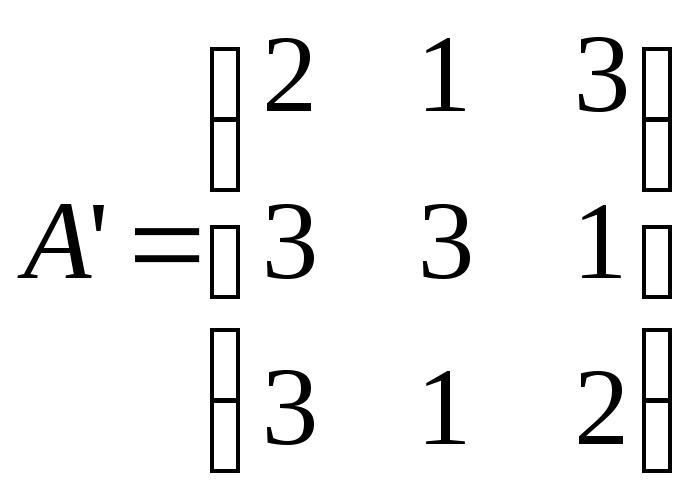 имеет положительные элементы. Найдем
оптимальные стратегии игроков в игре
имеет положительные элементы. Найдем
оптимальные стратегии игроков в игре![]() .
.
Выпишем задачу линейного программирования для второго игрока:
![]() ,
,
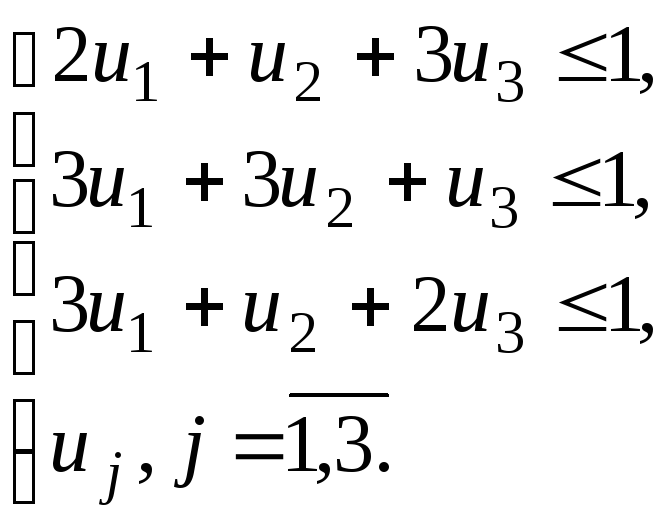 (5)
(5)
Каноническая форма задачи (5) имеет вид:
![]() ,
,

Таблица симплекс-метода решения задачи представлена ниже.
|
|
|
|
1 |
1 |
1 |
0 |
0 |
0 |
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
1 |
3 |
1 |
0 |
0 |
|
|
|
0 |
1 |
3 |
3 |
1 |
0 |
1 |
0 |
1/3 |
|
|
0 |
1 |
3 |
1 |
2 |
0 |
0 |
1 |
|
|
|
|
0 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
|
|
|
0 |
2/3 |
1 |
0 |
8/3 |
1 |
-1/3 |
0 |
1/4 |
|
|
1 |
1/3 |
1 |
1 |
1/3 |
0 |
1/3 |
0 |
|
|
|
0 |
2/3 |
2 |
0 |
5/3 |
0 |
-1/3 |
1 |
|
|
|
|
1/3 |
0 |
0 |
-2/3 |
0 |
1/3 |
0 |
|
|
|
1 |
1/4 |
3/8 |
0 |
1 |
3/8 |
-1/8 |
0 |
|
|
|
1 |
1/4 |
7/8 |
1 |
0 |
-1/8 |
3/8 |
0 |
|
|
|
0 |
1/4 |
11/8 |
0 |
0 |
-5/8 |
-1/8 |
1 |
|
|
|
|
1/2 |
1/4 |
0 |
0 |
1/4 |
1/4 |
0 |
|
Критерий
останова
![]() выполнен, оптимальным решением задачи
является вектор
выполнен, оптимальным решением задачи
является вектор![]() ,
оптимальное значение функции цели равно
,
оптимальное значение функции цели равно![]() .
Следовательно, цена игры
.
Следовательно, цена игры![]()
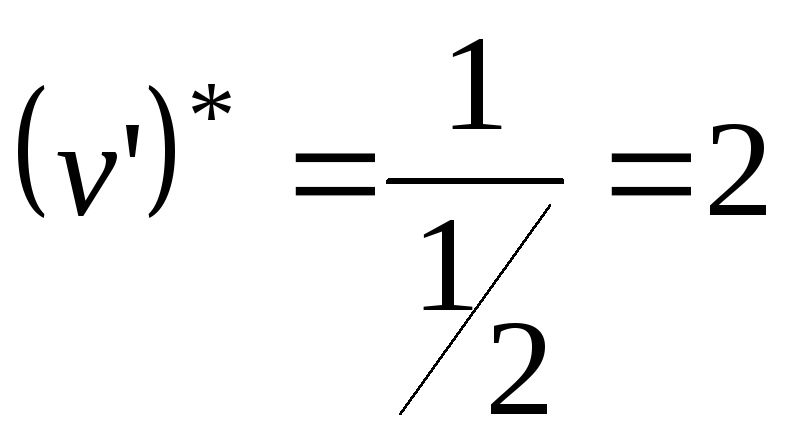 ,
а, согласно лемме о масштабе, цена
исходной игры
,
а, согласно лемме о масштабе, цена
исходной игры![]() .
Решение двойственной к (5) задачи находится
из симлексной таблицы как оценки
.
Решение двойственной к (5) задачи находится
из симлексной таблицы как оценки![]() ,
стоящие на последней итерации под
столбцами исходного базиса (в примере
,
стоящие на последней итерации под
столбцами исходного базиса (в примере![]() ,
,![]() ,
,![]() ).
Таким образом,
).
Таким образом,![]() .
Возвращаясь к исходным стратегиям
игроков, получаем:
.
Возвращаясь к исходным стратегиям
игроков, получаем:![]() ,
,![]() ,
,![]() ,
то есть
,
то есть![]() .
Аналогично
.
Аналогично![]() .
.
