
- •И.Н.Булгакова, ю.В.Бондаренко, г.Д.Чернышова
- •§ 1. Основные понятия исследования операций. Математическая модель операции
- •§ 2. Понятие игры. Классификация игр
- •§ 3. Антагонистические игры в нормальной форме
- •3.1 Определение антагонистической игры в нормальной форме. Матричные игры
- •Примеры
- •3.2 Ситуация равновесия в чистых стратегиях: понятие и существование
- •Упражнения к § 3.1. – 3.2
- •3.3 Смешанное расширение игры
- •3.4 Методы решения матричных игр
- •3. Сведение игры к задаче линейного программирования
- •3.5 Существование оптимальных стратегий. Теорема фон Неймана-Нэша
- •Упражнения к § 3.3–3.5
- •3.6. Доминирование стратегий
- •Примеры
- •Упражнения к § 3.6
- •3.7 Игры с частными случаями платежных матриц
- •§ 4. Игры в условиях неопределенности и риска (игры с природой)
- •Принятие решений в условиях полной неопределенности
- •Принятие решений в условиях риска
- •Примеры
- •Упражнения к § 4
- •§ 5 Позиционые игры
- •Упражнения
- •Список литературы
- •I. Основная литература
- •II. Дополнительная литература
Примеры
Пример 1. Используя понятие доминирования, упростить матрицу игры, если
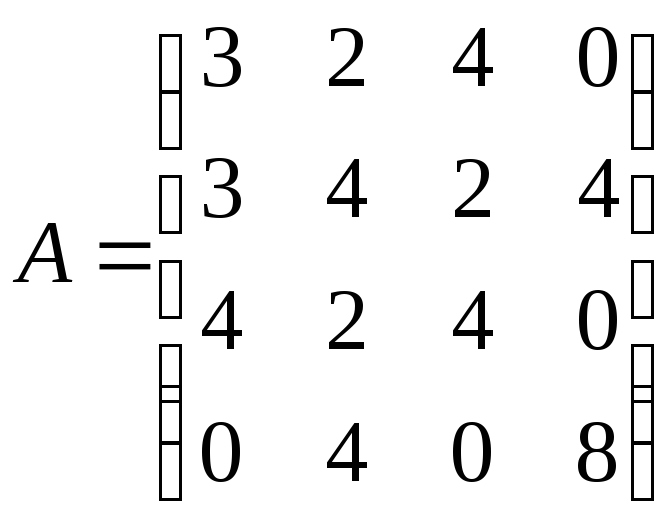 .
.
Решение
Рассмотрим первоначальную матрицу А, занумеровав стратегии игроков

Первоначально упростим матрицу игры, исключив чистые стратегии, доминируемые чистыми стратегиями.
Для игрока P1
стратегия
![]() доминирует стратегию
доминирует стратегию![]() так как, например,
так как, например,![]() ,
,![]() и, следовательно,
и, следовательно,![]() .
Аналогично для остальных элементов
этих строк выполнены неравенства:
.
Аналогично для остальных элементов
этих строк выполнены неравенства:![]() ,
,![]() .
Вычеркивая доминируемую стратегию,
переходим к матрице
.
Вычеркивая доминируемую стратегию,
переходим к матрице
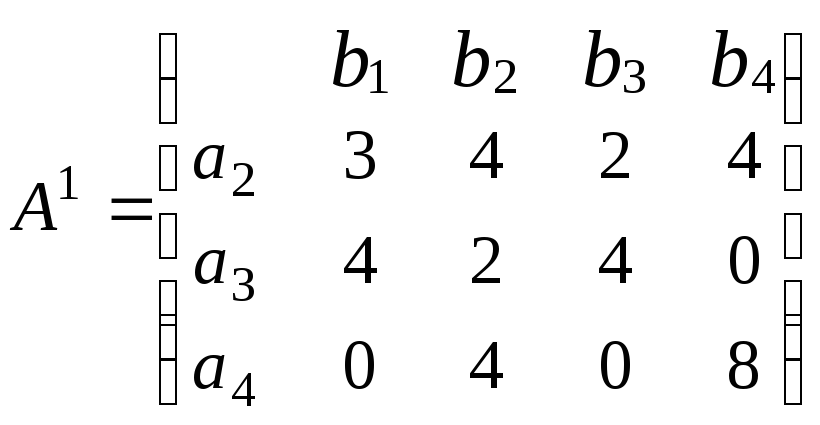
В матрице
![]() для стратегий
для стратегий![]() и
и![]() второго игрока выполнены неравенства:
второго игрока выполнены неравенства:![]() ,
,![]() .
Следовательно,
.
Следовательно,![]() доминирует
доминирует![]() .
.
Вычеркивая первый
столбец матрицы
![]() ,
получим
,
получим
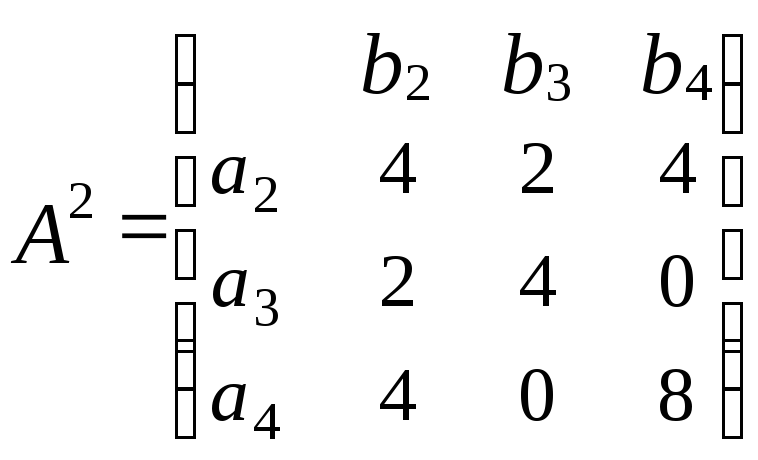 .
.
В матрице
![]() нет доминирования чистых стратегий
игроков чистыми стратегиями. Найдем
(если это возможно) те стратегии, которые
доминируются смешанными стратегиями
игроков.
нет доминирования чистых стратегий
игроков чистыми стратегиями. Найдем
(если это возможно) те стратегии, которые
доминируются смешанными стратегиями
игроков.
Рассмотрим игрока Р1.
Проверим, существует
ли смешанная стратегия игрока, доминирующая
стратегию
![]() .
Согласно лемме 4, в качестве такой
стратегии достаточно рассмотреть
.
Согласно лемме 4, в качестве такой
стратегии достаточно рассмотреть![]() и найти такое
и найти такое![]() ,
для которого выполнена система неравенств:
,
для которого выполнена система неравенств: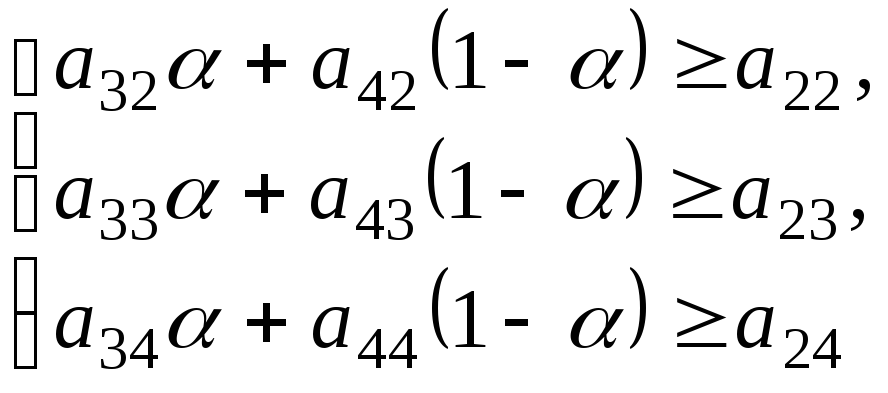 то есть
то есть
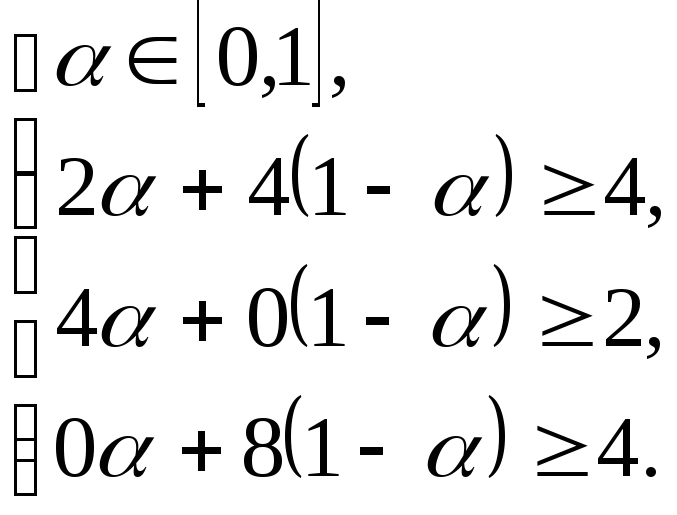
Из первого
неравенства системы следует, что
![]() ,
а так как
,
а так как![]() ,
то остается полагать, что
,
то остается полагать, что![]() .
Однако данное
.
Однако данное![]() не удовлетворяет второму неравенству
системы, а, следовательно, система не
имеет решения и чистая стратегия
не удовлетворяет второму неравенству
системы, а, следовательно, система не
имеет решения и чистая стратегия![]() не доминируется никакой смешанной.
не доминируется никакой смешанной.
Рассматривая
аналогично чистые стратегии
![]() и
и![]() приходим к выводу, что и они также не
домируются смешанными стратегиями.
приходим к выводу, что и они также не
домируются смешанными стратегиями.
![]() Проверим
наличие доминируемых стратегий у второго
игрока.
Проверим
наличие доминируемых стратегий у второго
игрока.
Проверим, существует
ли смешанная стратегия игрока
![]()
![]() ,
доминирующая стратегию
,
доминирующая стратегию![]() .
Найдем такое
.
Найдем такое![]() ,
для которого выполнена система неравенств:
,
для которого выполнена система неравенств: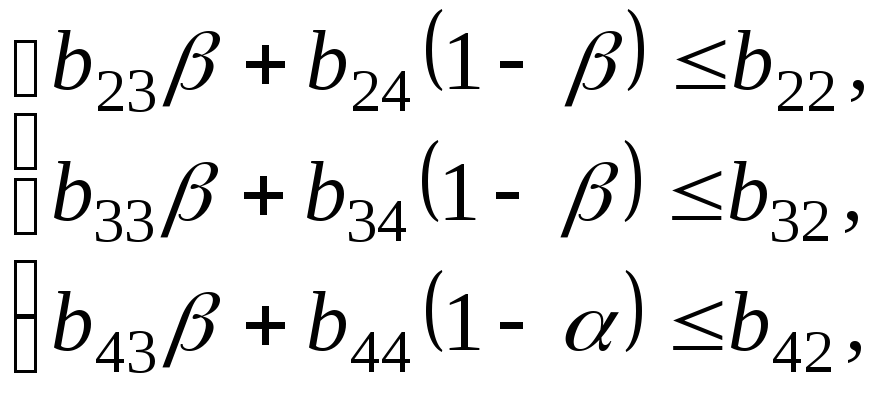 то есть
то есть
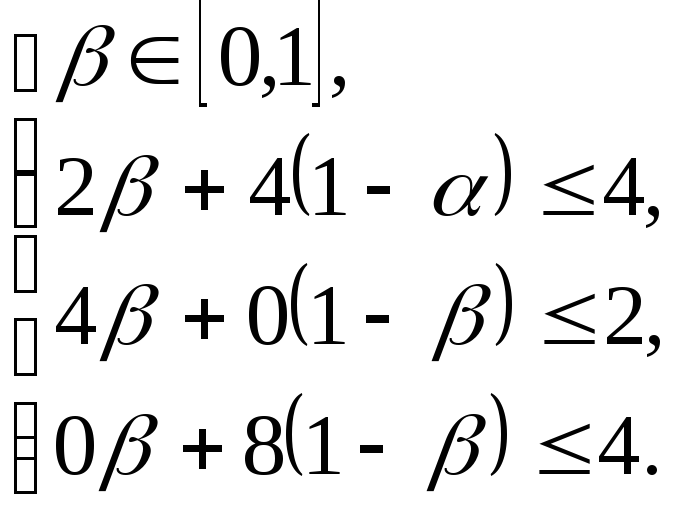
Решением системы
является
![]() .
Следовательно,
.
Следовательно,![]() доминирует
доминирует![]() .
Вычеркивая вторую стратегию второго
игрока, переходим к матрице
.
Вычеркивая вторую стратегию второго
игрока, переходим к матрице
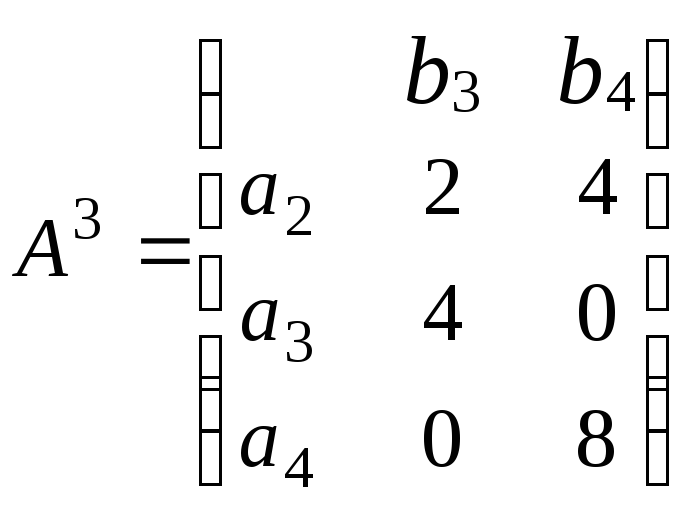 .
.
В матрице
![]() для первого игрока выполнены равенства:
для первого игрока выполнены равенства:![]() .
Следовательно, смешанная стратегия
.
Следовательно, смешанная стратегия![]() доминирует
доминирует![]() .
Вычеркивая
.
Вычеркивая![]() ,
получаем матрицу
,
получаем матрицу
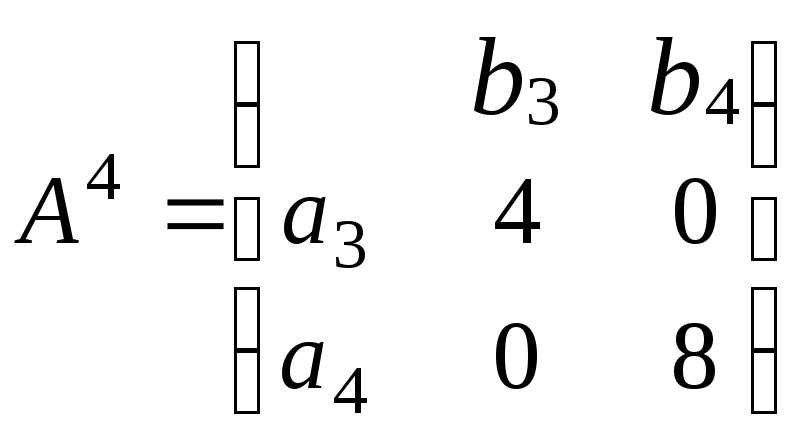 .
.
Решением игры
![]() являются стратегии
являются стратегии![]() ,
расширяя которые на 1 и 2 местах, получим
оптимальные стратегии исходной игры:
,
расширяя которые на 1 и 2 местах, получим
оптимальные стратегии исходной игры:![]() .
.
Упражнения к § 3.6
№ 1. Найти оптимальные стратегии игроков, предварительно упростив матрицу игры, используя понятие доминирования, если матрица игры имеет вид:
1)
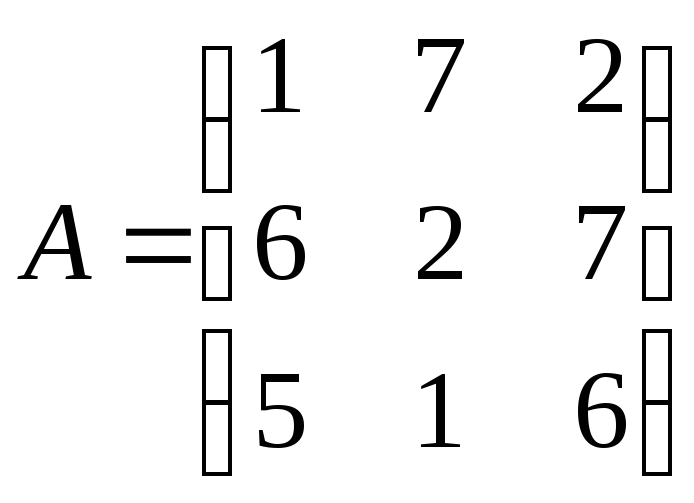 ;
2)
;
2)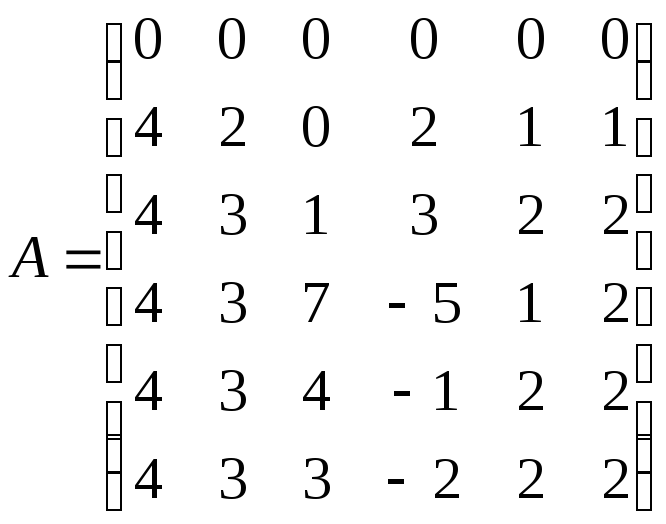 ;
3)
;
3)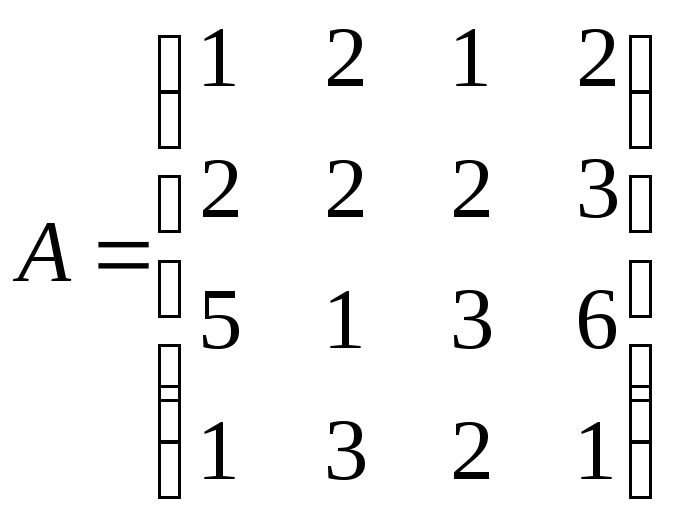 ;
4)
;
4)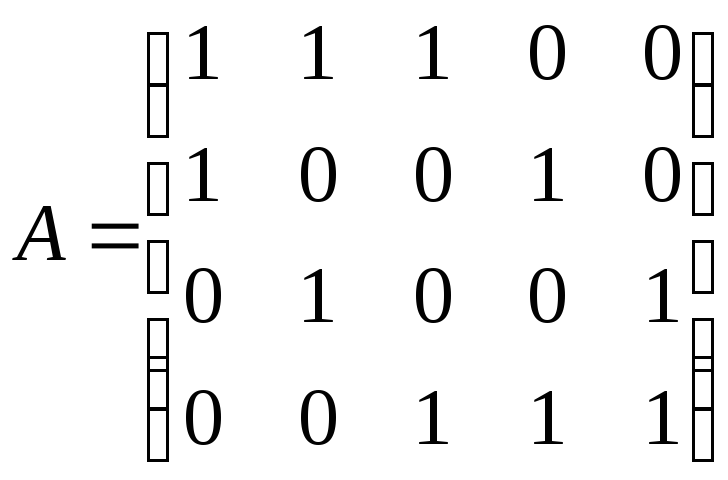 .
.
№ 2. Найти оптимальные стратегии игроков: 1) непосредственно используя свойство 2 оптимальных стратегий; 2) предварительно упростив матрицу, используя понятие доминирования. Совпадут ли множества оптимальных стратегий, полученные данными способами? Если нет, то объяснить почему.
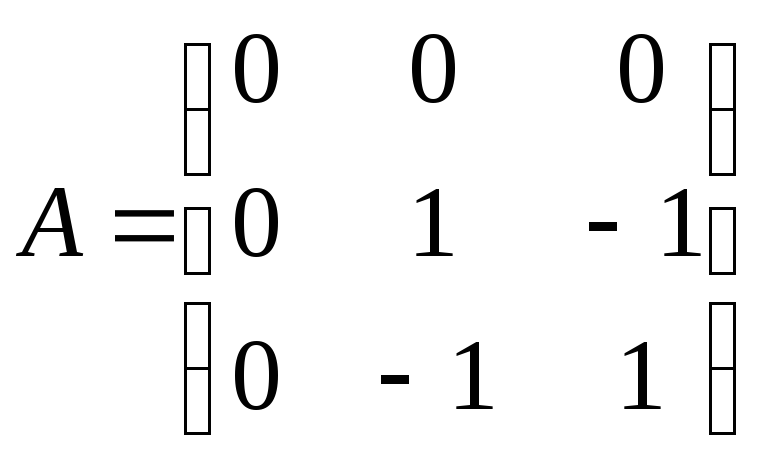 .
.
3.7 Игры с частными случаями платежных матриц
Диагональная игра
Примером диагональной
игры может служить игра в «прятки»,
состоящая в следующем. 2-й игрок прячется
в одну из n
ячеек, а 1-й игрок обследует одну из них.
Если он выбрал ячейку i и 2-й игрок
находится там, то 1-й игрок обнаруживает
2-го игрока с вероятностью
![]() в
противном случаевероятностьобнаружения равна нулю. Целью 1-го игрока
является максимизация, а целью 2-го
минимизация вероятности обнаружения.
Эта игра описывается диагональной
матрицей
в
противном случаевероятностьобнаружения равна нулю. Целью 1-го игрока
является максимизация, а целью 2-го
минимизация вероятности обнаружения.
Эта игра описывается диагональной
матрицей
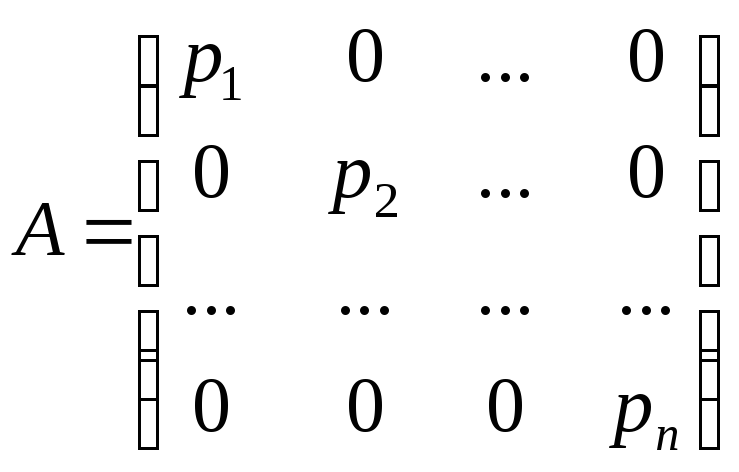 .
.
Стратегии оптимальные игроков здесь совпадают; они состоят в выборе ячеек с вероятностями, равными
 ,
,
![]()
Симметричная игра
Определение.
Квадратрная
матрица
![]() называется кососимметрической, если
называется кососимметрической, если![]() для всех
для всех![]() ,
,![]() .
Матричная игра называется симметричной,
если еематрица коссосиметрическая.
.
Матричная игра называется симметричной,
если еематрица коссосиметрическая.
Теорема.
Знгачение симметричной игры равно нулю.
Кроме того, если
![]() есть
оптимальная стратегия для первого
игрока, то
есть
оптимальная стратегия для первого
игрока, то
![]() есть также оптимальная стратегия для
второго игрока.
есть также оптимальная стратегия для
второго игрока.
Доказательство.
Пусть
![]() - матрица игры и
- матрица игры и
![]() -произвольная
стратегия. Легко видеть, что
-произвольная
стратегия. Легко видеть, что
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Поэтому
![]() .
Отсюда следует, что для любого
.
Отсюда следует, что для любого
![]()
![]() .
.
так что значение игры неположительно.
В тоже время
![]() ,
,
так что значение
игры неотрицательно. Следовательно,
значение игры равно нулю. Далее, если
![]() - оптимальная
стретегия первого игрока, то
- оптимальная
стретегия первого игрока, то
![]() .
.
Но отсюда
![]() ,
,
так что
![]()
или
![]() .
.
Значит, стратегия
![]() оптимальная
также и для второго игрока.
оптимальная
также и для второго игрока.
Пример. («камень–ножницы–бумага»). Каждый игрок во время своего хода независимо от другого выбирает одну из трех стратегий, называемых «камень», «ножницы» и «бумага». Выбранные стратегии сравниваются. Если они совпадают, выигрыш первого игрока составляет 0 (ничья), в противном случае побеждает игрок с более сильной стратегией. «Камень» считается сильнее «ножниц», которые, в свою очередь, сильнее «бумаги», которая сильнее «камня». Выигрыш победившего игрока составляет 1, проигравшего -1. Платежная матрица в этом случае имеет следующий вид:
 .
.
Так как матрица
кососимметрическая, значение игры
должно быть равно нулю. Очевидно, эта
игра не имеет седловой точки. Кроме
того, оптимальная стратегия не может
использовать только две чистые стратегии.
Действительно, если, например,
![]() ,
,
![]() и
и
![]() ,
то легко видеть, что такая смешанная
стратегия для первого игрока дает
отрицательный ожидаемый выигрыш против
первой чистой стратегии второго игрока.
Поэтому все компоненты оптимальной
стратегии
,
то легко видеть, что такая смешанная
стратегия для первого игрока дает
отрицательный ожидаемый выигрыш против
первой чистой стратегии второго игрока.
Поэтому все компоненты оптимальной
стратегии
![]() будут
положительными. Эта стратегия оптимальна
также и для второго игрока, и компоненты
вектора
будут
положительными. Эта стратегия оптимальна
также и для второго игрока, и компоненты
вектора
![]() должны
удовлетворять системе линейных уравнений
должны
удовлетворять системе линейных уравнений
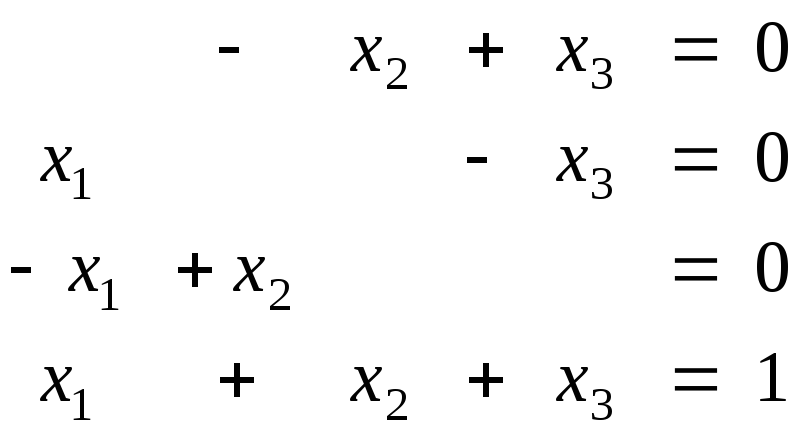 .
.
Решение этих
уравнений
![]() нетрудно найти. Для обоих игрокой это
единственная оптимальная стратегия.
нетрудно найти. Для обоих игрокой это
единственная оптимальная стратегия.
