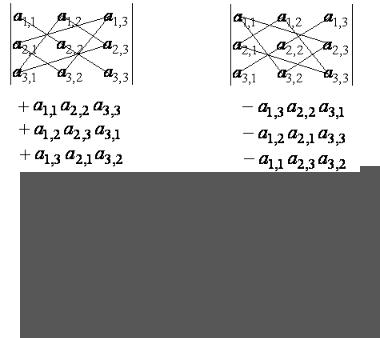
Определители
Первые три перестановки являются четными, поскольку каждая из них содержит четное число инверсий.
Оставшиеся три перестановки являются нечетными, так каждая из них содержит нечетное число инверсий. (См. пример на стр. 22.)
Таким образом,
a1,1 a1,2 a1,3
a2,1 a2,2 a2,3 = a1,1a2,2a3,3 +a1,2a2,3a3,1 +a1,3a2,1a3,2 a3,1 a3,2 a3,3
−a1,3a2,2a3,1 −a1,2a2,1a3,3 −a1,1a2,3a3,2
Эту формулу можно легко запомнить с помощью правила треугольников, которое иллюстрируется нижеприведенным рисунком.
Элементы, стоящие на диагоналях или в вершинах треугольников, основания которых параллельны диагоналям, образуют произведения трех элементов. Если основание треугольника параллельно главной диагонали матрицы, то произведение элементов сохраняет свой знак. Если же основание треугольника параллельно побочной диагонали матрицы, то произведение элементов берется с противоположным знаком.
2.3.Свойства определителей
1.Определитель транспонированной матрицы равен определителю исходной матрицы:
det AT = det A .
Это свойство выражает равноправие строк и столбцов определителя. Доказательство: Свойство вытекает из определения детерминанта – оба детерминанта представляют собой суммы одних и тех же элементов.
2.Умножая строку или столбец определителя на число λ, мы умножаем определитель на это число:
25
Определители
Можно сказать и так: Общий множитель строки (или столбца) можно выносить за знак определителя.
Доказательство: При умножении строки определителя на число один из сомножителей в произведении a1,k1 a2,k2 Kan,kn (−1)P{k1, k2 , K, kn }
умножается на это число. Это число входит в виде общего множителя в каждое слагаемое суммы
det A = ∑a1,i1 a2,i2 Kan,in (−1)P{i1 ,i2 ,K,in } . {i1 ,i2 ,K,in }
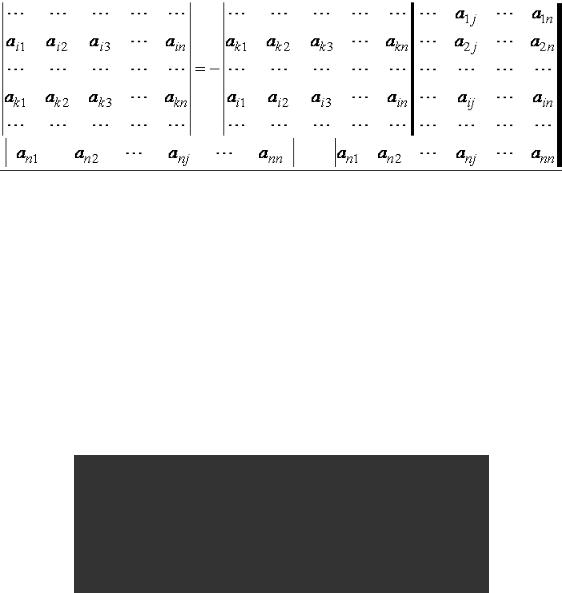
3.Определитель изменяет свой знак при перестановке местами любых двух строк (или столбцов) определителя.
Доказательство: По Теореме 1, транспозиция изменяет четность перестановки. Следовательно, каждое слагаемое суммы
det A = ∑a1,i1 a2,i2 Kan,in (−1)P{i1 ,i2 ,K,in } {i1 ,i2 ,K,in }
изменяет свой знак на противоположный.
4.Если матрица имеет нулевую строку (столбец), то определитель этой матрицы равен нулю:
26
Определители
L |
L |
L |
L |
L |
|
ai,1 |
ai,2 |
ai,3 |
L ai,n |
|
|
0 |
0 |
0 |
L |
0 |
= 0 |
a j,1 |
a j,2 |
a j,3 |
L a j,n |
|
|
L |
L |
L |
L |
L |
|
Доказательство: Нуль является общим множителем строки (столбца) и, следовательно, общим множителем определителя.
5.Если две строки (столбца) матрицы равны между собой, то определитель этой матрицы равен нулю:
L L L L L
ai,1 ai,2 ai,3 L ai,n
L L L L L = 0
ai,1 ai,2 ai,3 L ai,n
L L L L L
Доказательство: По Свойству 3 при перестановке двух строк местами определитель изменяет свой знак. С другой стороны, перестановка местами одинаковых строк не меняет определитель. Следовательно,
det A = −det A det A = 0.
6.Если две строки (столбца) матрицы пропорциональны друг другу, то определитель этой матрицы равен нулю:
L |
L |
L |
L |
L |
|
ai,1 |
ai,2 |
ai,3 |
L ai,n |
|
|
L |
L |
L |
L |
L |
= 0 |
cai,1 cai,2 |
cai,3 |
L cai,n |
|
||
L |
L |
L |
L |
L |
|
|
|
|
|
|
|
Доказательство: Вынося общий множитель пропорциональности в строке за знак определителя, мы получаем определитель, имеющий две одинаковых строки. Согласно Свойству 5 такой определитель равен нулю.
7.Определитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали:
27
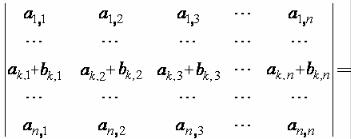
Определители
a1,1 |
a1,2 |
a1,3 |
L a1,n |
|
|
0 |
a2,2 |
a2,3 |
L a2,n |
|
|
0 |
0 |
a3,3 |
L a3,n |
= a1,1 a2,2 a3,3 K an,n . |
|
L |
L |
L |
L |
L |
|
0 |
0 |
0 |
L |
an,n |
|
В частности, определитель единичной матрицы E равен 1.
Доказательство: По определению, det A представляет собой алгебраическую сумму произведений элементов (с учетом правила выбора знаков), составленных так, чтобы каждая строка и каждый столбец матрицы A были представлены в произведении одним и только одним элементом.
В первом столбце имеется только один ненулевой элемент, а именно
a1,1 .
Во втором столбце в нашем распоряжении остается только один ненулевой элемент a2,2 , поскольку первая строка уже представлена
своим элементом. При любой другом выборе соответствующее произведение обращается в нуль.
Аналогично, в третьем столбце мы можем остановить свой выбор только на элементе a3,3 и т.д.
Таким образом, сумма (2) содержит только одно ненулевое слагаемое, которое равно произведению элементов, стоящих на главной диагонали.
8.Если каждый элемент строки (столбца) определителя представлен в виде суммы двух членов, то
28
Определители
Доказательство: Преобразуем исходный определитель:
∑a1,i1 K(ak,ik +bk ,ik )Kan,in (−1)P{i1,i2 ,K,in} =
{i1,i2 ,K,in}
= ∑Kak,ik K + ∑Kbk,ik K=
{i1,i2 ,K,in} {i1,i2 ,K,in}
9.Определитель не изменится, если к одной из его строк прибавить другую, предварительно умноженную на любое число:
L |
L |
L |
L |
L |
|
L |
L |
L L |
L |
ai,1 |
ai,2 |
ai,3 |
L ai,n |
|
ai,1 |
ai,2 |
L L ai,n |
||
L L L |
L L |
= |
L |
L L L L |
|||||
ak ,1 |
ak ,2 |
ak ,3 |
L ak ,n |
|
ak ,1 + cai,1 |
ak ,2 + cai,2 |
L L ak ,n + cai,n |
||
L |
L |
L |
L |
L |
|
L |
L |
L L |
L |
|
|
|
|
|
|
|
|
|
|
Доказательство: Определитель, стоящий в правой части равенства, можно представить в виде суммы двух определителей, один из которых является исходным, а второй имеет две пропорциональные друг другу строки и, следовательно, равен нулю.
10.Пусть A и B – квадратные матрицы одного и того же порядка. Тогда определитель произведения матриц равен произведению определителей:
det(AB) =det A det B .
29
Определители |
|
|
|
|
|
|
|
|
|
Примеры. |
|
|
|
|
|
|
|
|
|
1) Вычислить |
|
sin x |
cos x |
|
. |
||||
|
|
||||||||
|
−cos x |
sin x |
|
||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
sin x |
cos x |
|
=sin x sin x −cos x (−cos x) =sin2 x + cos2 x =1. |
|||||
|
|
||||||||
|
−cos x |
sin x |
|
|
|
|
|
||
2)Для данной матрицы A = a
c
тождества det A = det AT .
Решение: |
|
|
|
||
det A = |
|
a |
b |
|
= ad −bc |
|
|
||||
|
|
c |
d |
|
|
b убедиться в справедливости d
и |
det AT = |
|
a |
c |
|
= ad −bc. |
|
|
|||||
|
b |
d |
|
3) Вычислить |
1 |
2 |
3 |
|
4 |
5 |
6 |
. |
|
|
7 |
8 |
9 |
|
Решение: Преобразуем определитель, вычитая из второй строки удвоенную первую, а из третьей – утроенную первую.
1 |
2 |
3 |
r2 |
→r2 |
−2r1 |
1 |
2 |
3 |
|
4 |
5 |
6 |
r3 |
→r3 |
−3r1 |
2 |
1 |
0 |
. |
|
= |
||||||||
7 |
8 |
9 |
|
|
|
4 |
2 |
0 |
|
Вынося из третьей строки общий множитель 2, мы получаем определитель, имеющий две одинаковых строки:
1 |
2 |
3 |
|
1 |
2 |
3 |
|
2 |
1 |
0 |
= 2 |
2 |
1 |
0 |
=0 . |
4 |
2 |
0 |
|
2 |
1 |
0 |
|
4) Пусть |
5 |
0 |
|
7 |
1 |
|
||
A = |
1 |
2 |
и |
B = |
3 |
2 |
. Убедиться в справедливости |
|
|
|
|
|
|
||||
тождества det AB =det A det B.
Решение:
30
Определители
|
|
det A = |
|
5 |
0 |
|
=10 , |
det B = |
|
|
7 |
1 |
|
=11, |
|||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
det A det B =110 . |
|
|
|
|||||||||||||
|
|
|
|
AB = |
5 0 7 1 |
|
35 5 |
||||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
, |
|||||||||||
|
|
|
|
|
|
|
|
|
1 2 3 2 |
|
13 5 |
||||||||||||||
|
det AB = |
|
35 |
5 |
|
= |
5 |
|
35 |
1 |
|
=5(35 −13) =110 . |
|||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
13 |
5 |
|
|
|
|
|
|
13 |
1 |
|
|
|
|
|
|
|
|
|||
5) |
Вычислить det A1000 , если |
|
|
3 |
1 |
|
|
|
|
|
|
||||||||||||||
A = |
2 |
|
. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Решение: Заметим, что |
det A1000 =(det A)1000 |
|
|
|
|||||||||||||||||||||
Далее, |
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
det A = |
= 3 −2 =1 |
|
|
|
det A1000 =11000 =1. |
|||||||||||||||||||
|
2 |
1 |
|
|
|||||||||||||||||||||
|
2 |
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
6) |
|
0 |
|
1 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пусть A = |
|
|
. Вычислить: |
|
|
|
|
|
|
||||||||||||||||
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
(a) det A, |
|
|
|
|
|
(b) det A3 , |
|
|
|
(c) det(2A) , |
||||||||||||||
|
(d) det(−3A) , |
|
|
|
|
(e) |
det(A − 2E) . |
|
|
|
|
|
|
||||||||||||
Решение:
(a)Определитель матрицы треугольного вида равен произведению диагональных элементов.
Таким образом,
2 3 4
det A = 0 1 5 = 2 1 (−1) = −2 .
00 −1
(b)Определитель произведения матриц равен произведению определителей. Следовательно,
det A3 = (det A)3 = (−2)3 = −8.
(c) Представим матрицу 2A в виде 2E A, где E– единичная матрица. Тогда
31