Тема 6 Средние величины и показатели вариации.

1. Понятие о средних величинах.

2. Виды средних и способы их вычисления.

3. Понятие о средних величинах.

1. Понятие о средних величинах.

Многие признаки единиц статистической совокупности различны по своему значению и поэтому, чтобы определить значение признака, характерное для всей изучаемой совокупности единиц, прибегают к расчету средних величин.

Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности. В экономической практике используется широкий круг показателей, вычисленных в виде средних величин.

Вычисление среднего – один из распространенных приемов обобщения; средний показатель отражает то общее, что характерно (типично) для всех единиц совокупности, в то же время он игнорирует различия отдельных единиц. Значения признака отдельных единиц совокупности варьируют под влиянием множества факторов, среди которых могут быть как основные, так и случайные. Сущность средней в том и заключается, что в ней взаимопогашаются те отклонения значений признака, которые обусловлены действием случайных факторов, и учитываются изменения, вызванные действием факторов основных.

Принципы применения средних величин:

1. При определении средней величины в каждом конкретном случае нужно исходить их качественного содержания осредняемого признака, учитывать взаимосвязь изучаемых признаков, а также имеющиеся для расчета данные.

2. Средняя величина должна прежде всего рассчитываться по однородной совокупности.

3. Общие средние должны подкрепляться групповыми средними.

4. Необходим обоснованный выбор единицы совокупности, для которой рассчитывается средняя.

Однако нельзя сводить роль средних только к характеристики типических значений признаков в однородных по данному признаку совокупностях. На практике современная статистика использует так называемые системные средние, обобщающие неоднородные явления – средний национальный доход на душу населения, средняя урожайность зерновых по стране и т. д. Системные средние могут характеризовать как пространственные или объектные системы, существующие одномоментно государство, отрасль, регион, планета Земля), так и динамические системы, протяженные во времени (год, десятилетие, сезон и т. п.).

Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.

2. Виды средних и способы их вычисления.

Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. Он состоит из нескольких этапов:

1) устанавливается определенный показатель, т.е. обобщающий показатель совокупности, от которого зависит величина средней;

2) определяется математическое выражение для определяющего показателя;

3) производиться замена индивидуальных значений средними величинами;

4) решение уравнения средней.

Основополагающее правило при этом заключается в том, что величины, представляющие собой числитель и знаменатель средней, должны иметь определенный логический смысл.

Средние величины делятся на больших класса:

- степенные средние;

- структурные средние.

К степенным средним относятся средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, средняя кубическая.

В качестве структурных средних рассматриваются мода и медиана.

Степенные средние объединяются общей формулой:

,

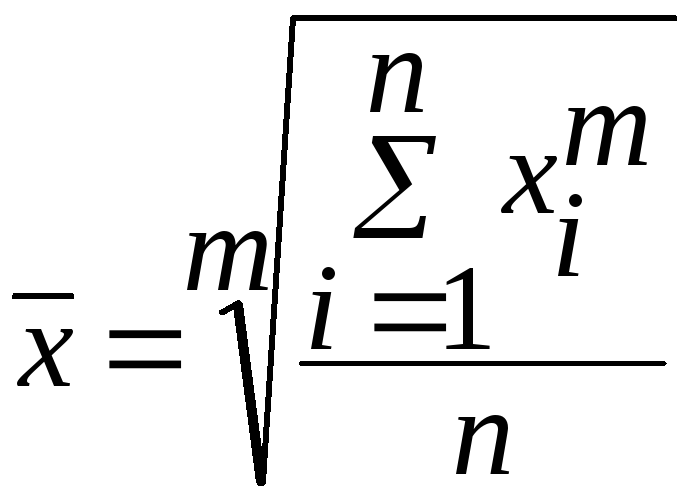- среднее значение исследуемого явления;

m – показатель степени средней;

x – текущее значение (вариант) осредняемого признака;

n – число признаков.

В зависимости от значения показателя степени m различают следующие виды средних:

При m =-1 – средняя гармоническая;

При m = 0 – средняя геометрическая;

При m = 1 – средняя арифметическая;

При m = 2 – средняя квадратическая;

При m = 3 – средняя кубическая.

При использовании одних и тех же исходных данных, чем больше m в формуле, тем больше значение средней величины:

.

Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется правилом мажоритарности средних.

В зависимости от представления исходных данных степенные средние могут быть простыми и взвешенными. Простая средняя рассчитывается по не сгруппированным данным и имеет следующий вид:

.

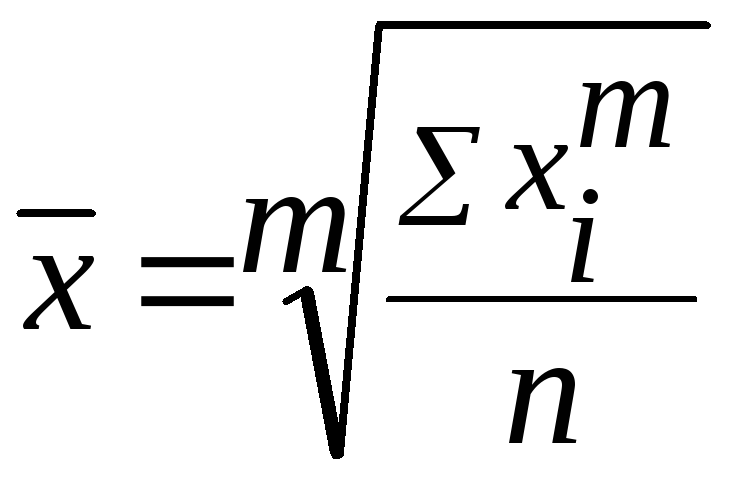Взвешенная средняя считается по сгруппированным данным и имеет общий вид:

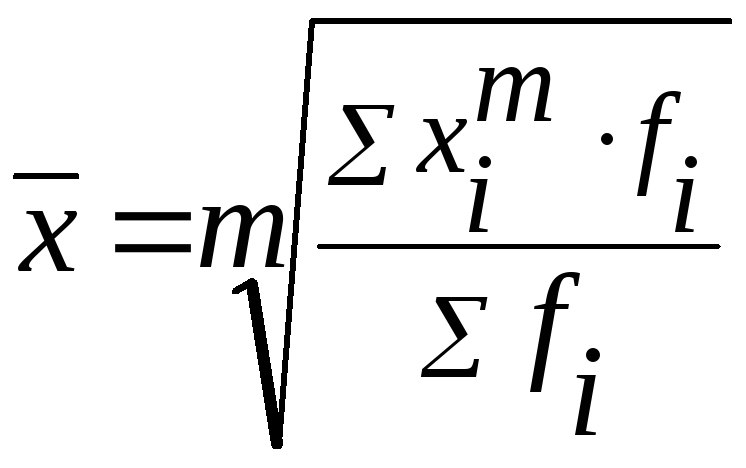
где x_i - значение (варианта) осредняемого признака;

m – показатель степени средней;

f_i - частота (вес), показывающая сколько раз встречается i – е значение осредняемого признака.

Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объём признака в совокупности сохраняется неизменным. Средняя арифметическая применяется в форме простой средней и взвешенной средней.

Средняя арифметическая простая равна сумме отдельных значений осредняемого признака, деленной на общее число этих значений:

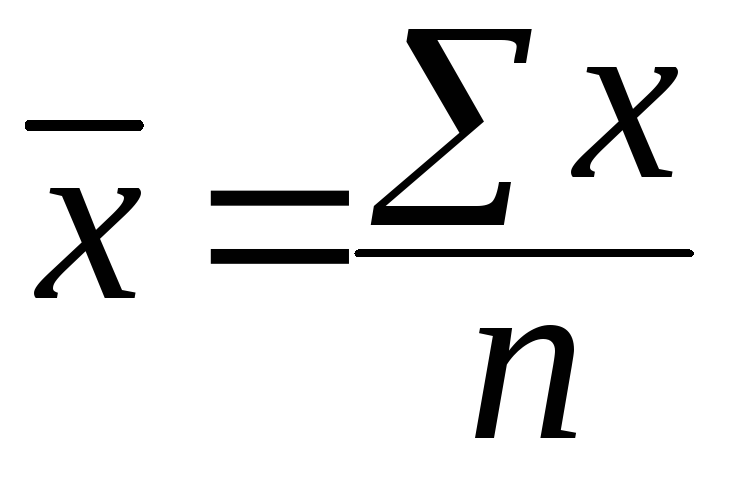
Она применяется в тех случаях, когда имеются не сгруппированные индивидуальные значения признака.

Средняя арифметическая взвешенная вычисляется по формуле:

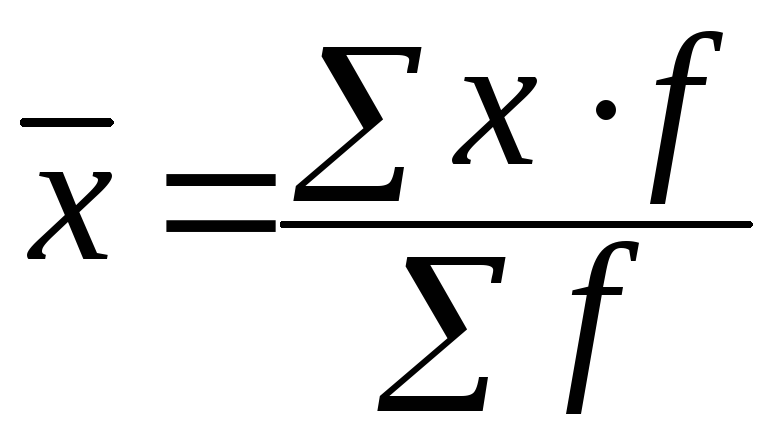
Она применяется в тех случаях, когда известны варианты, имеющие неравновеликие частоты (f).

Технику вычисления средней арифметической величины рассмотрим на примере расчета среднего возраста студентов в группе из 20 человек.

№ п/п	Возраст (лет)	№ п/п	Возраст (лет)	№ п/п	Возраст (лет)	№ п/п	Возраст (лет)
1	18	6	20	11	22	16	21
2	18	7	19	12	19	17	19
3	19	8	19	13	19	18	19
4	20	9	19	14	20	19	19
5	19	10	20	15	20	20	19

Средний возраст рассчитывается по формуле по формуле простой средней:

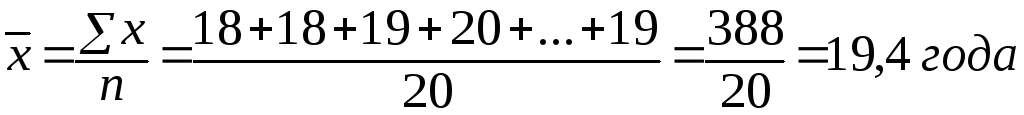
Сгруппируем исходные данные. Получим ряд распределения:

Возраст, x лет	18	19	20	21	22	Всего
Число студентов, f	2	11	5	1	1	20

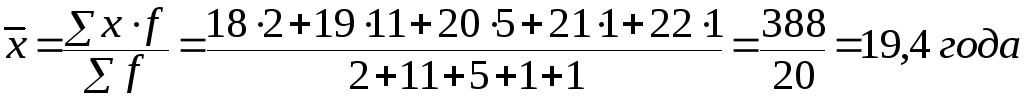
Средняя гармоническая – это величина обратная среднеарифметической.

В тех случаях, когда вес каждого варианта равен единице, применяется средняя гармоническая простая, исчисляемая по формуле:

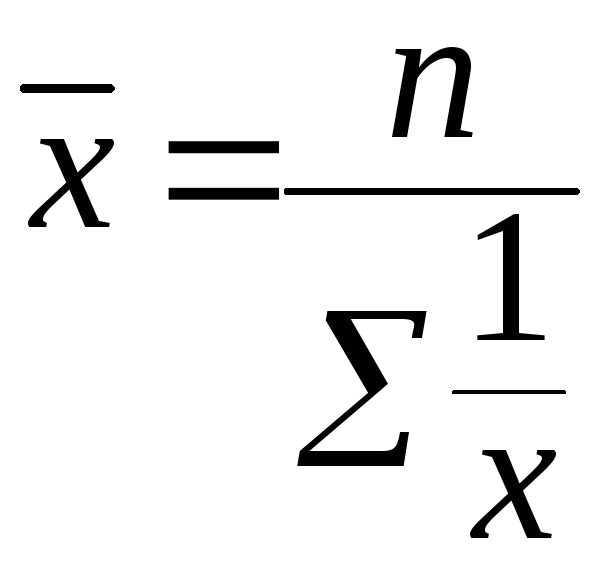
Когда статистическая информация не содержит частот fпо отдельным вариантамx совокупности, а представлена как их произведениеx*f, применяется формула средней гармонической взвешенной.

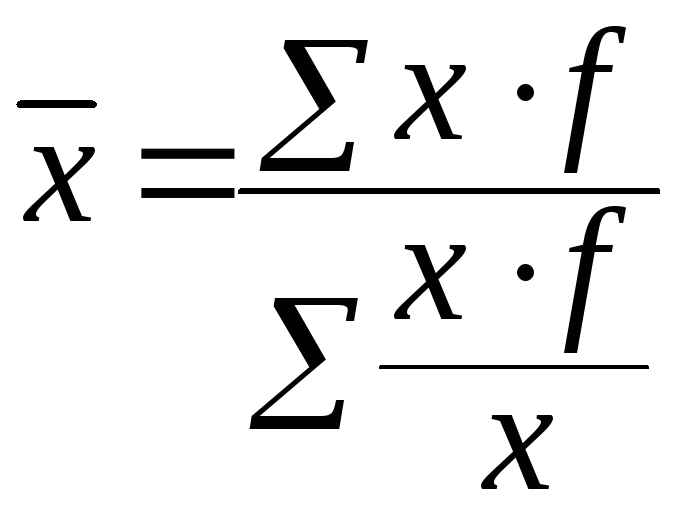
Средняя геометрическая применяется в тех случаях, когда необходимо сохранить неизменным произвдениее индивидуальных величин.

Средняя геометрическая простая имеет следующий вид:

где- знак произведения,n– число вариантов, периодов.

Средняя геометрическая взвешенная имеет следующий вид:

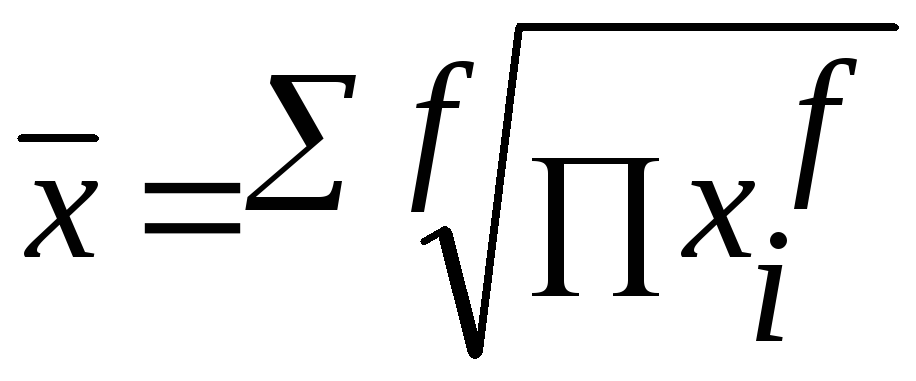
Средняя квадратическая применяется, когда необходимо рассчитать средний размер признака, выраженный в квадратных единицах измерения.

Средняя квадратическая простая имеет вид:

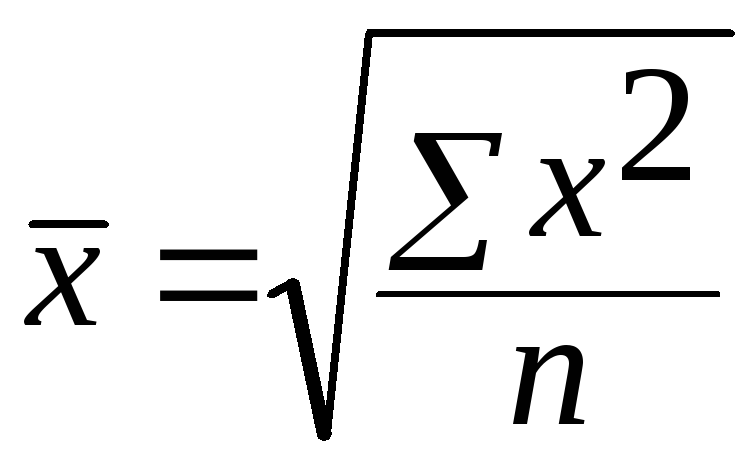
Средняя квадратическая взвешенная имеет вид:

.

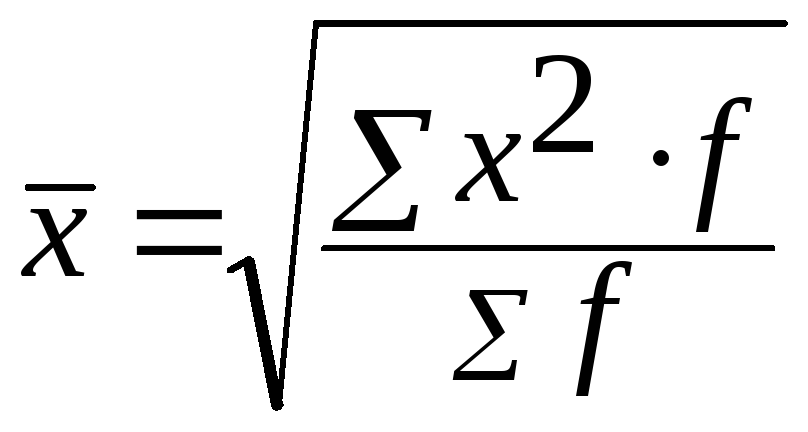Средняя кубическая применяется, когда необходимо рассчитать средний размер признака, выраженный в кубических единицах измерения.

Средняя кубическая простая имеет вид:

.

Средняя кубическая взвешенная имеет вид:

.

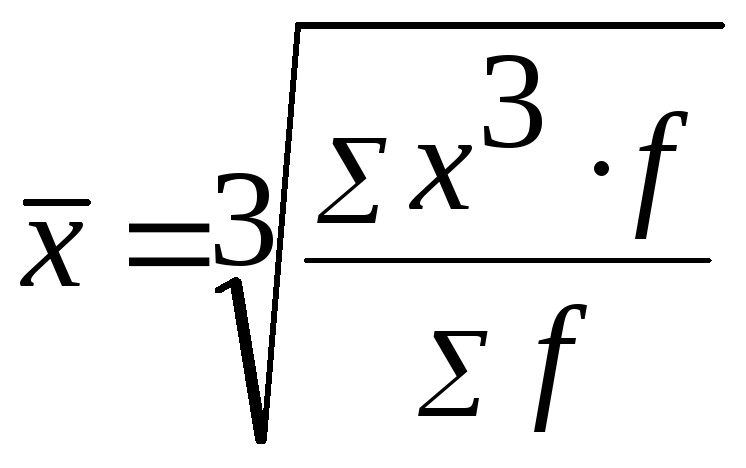Рассмотрим структурные средние.

Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

Мода Мо наиболее часто встречаемое значение признака.

В дискретном вариационном ряду – вариант, имеющий наибольшую частоту.

В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:

,

где x_мо- начало модального интервала; модальный интервал определяется по наибольшей частоте.

i_мо - модальный интервал;

f_мо f_мо-1 f_мо+1- частота модального, до и послемодального интервалов соответственно.

В случае неравных интервалов применяется следующая формула:

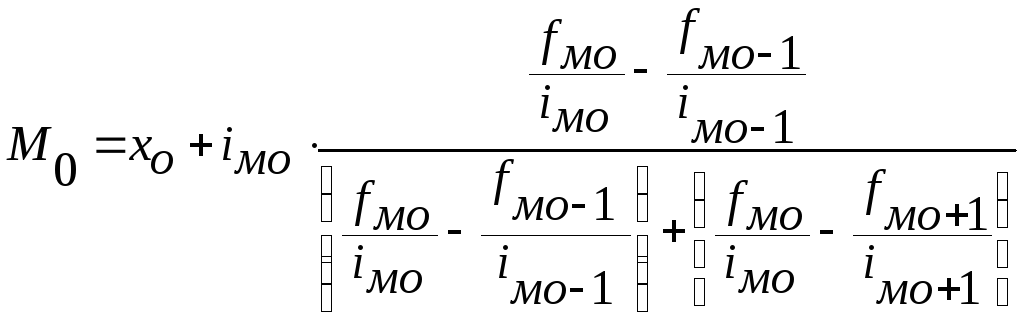
где x_мо- начало модального интервала, модальный интервал – интервал, в котором достигает максимума величина(плотность) – отношение частоты интервала к его величине;

i_мо, i_мо-1, i_мо+1- величина соответственно модального, до и послемодального интервалов.

Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т. п.

Медиана Ме– величина признака, которая делит упорядоченную последовательность его значений на две равные по численности части, т. е. со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану необходимо отыскать значение признака, которое находиться в середине упорядоченного ряда.

Для определения медианы в вариационном ряду необходимо вначале найти номер медианы: .

Затем используют накопленные частоты (сумму последовательно сложенных частот между собой).

В дискретном ряду распределения медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.

В интервальных рядах распределения медианное значение рассчитывается по формуле:

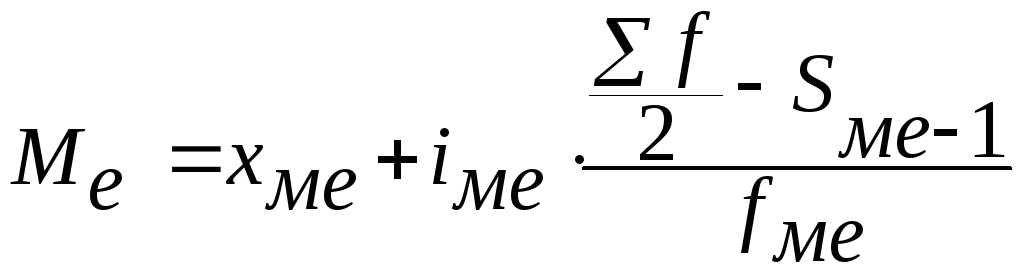
где x_ме- нижняя граница медианного интервала; медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений.

i_ме - медианный интервал;

- половина от общего числа наблюдений;

S_ме-1- сумма наблюдений, накопленная до начала медианного интервала;

f_ме - число наблюдений в медианном интервале.

Мода и медиана в отличие от степенных средних являются конкретными характеристиками, их значения имеют какой-либо конкретный вариант в вариационном ряду.

Рассмотрим на примерах расчет моды и медианы.

Пример 1.

Распределение семей города по числу детей характеризуется следующими данными:

Число детей в семье	0	1	2	3	4	5	Итого
Число семей	10	26	29	17	13	5	100

Определить моду и медиану.

Наибольшая частота (29 изделий) приходится на семью с 2 детьми. Следовательно, М_о = 2.

Для определения медианы нужно вначале найти номер медианы:

N_ме==

Затем используют накопленные частоты.

Накапливаем частоты до тех пор, пока накопленная частота не будет равна этому номеру или превысит его.

Число детей в семье	0	1	2	3	4	5	Итого
Число семей	10	26	29	17	13	5	100
Накопленная частота	10	36	65	82	95	100	-

Следовательно, 10 семей не имеют детей, 36 (10+26) семей имеют не более 1 ребенка, 65 (36+29) не более 2 детей, 82 (65+17) не более 3 детей и т. д. Т. о, медиана данного ряда распределения равна 2 детям в семье, т. е. половина семей имеют до 2 детей, а другая свыше 2-х детей.

М_е = 4 балла.

Пример 2.

Распределение длины пробега автофургона торговой фирмы характеризуется следующими данными:

Длина пробега за 1 рейс, км.	30-40	40-50 26	50-60 20	60-70 14 100	70-80	80 и выше	Итого
Число рейсов за 1 месяц	15	25	19	18	8	5	90

Определите модальное и медианное значение длины пробега за 1 рейс.

Модальным в данном распределении является интервал 40-50 км., так как наибольшее число рейсов (f = 25) находится в этом интервале.

Определим медианный интервал:

N_ме==

Затем используют накопленные частоты.

Длина пробега за 1 рейс, км.	30-40	40-50 26	50-60 20	60-70 14 100	70-80	80 и выше	Итого
Число рейсов за 1 месяц	15	25	19	18	8	5	90
Накопленная частота	15	40	59	77	85	90	-

Медианным считается интервал 50-60 км., так как в этом интервале находятся номер медианы.

Половина рейсов за месяц были протяженностью до 53 км., а другая половина свыше 53 км.