
diff_calc_econ_ua
.pdfМІНІСТЕРСТВО ОСВІТИ УКРАЇНИ
ХАРКІВСЬКИЙ ДЕРЖАВНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ БУДІВНИЦТВА ТА
АРХІТЕКТУРИ
Диференціальне числення
функції одної змінної
Навчально-методичний посібник
Харків ХДТУБА 2002
1
Зміст
1 Похідна та її застосування................................................................................................ |
3 |
||
1.1 |
Означення похідної, її геометричне та механічне тлумачення |
3 |
|
1.1.1 |
Означення похідної |
3 |
|
1.1.2 |
Геометричне тлумачення похідної |
5 |
|
1.1.3 |
Механічне тлумачення похідної |
5 |
|
1.1.4 |
Економічний зміст похідної |
6 |
|
1.2 |
Рівняння дотичної і нормалі до кривої |
7 |
|
1.3 |
Задача про продуктивність труда |
9 |
|
1.4 |
Основні правила диференціювання функцій |
9 |
|
1.5 |
Диференціювання складної функції |
19 |
|
1.6Диференціювання функцій, заданих неявно та параметрично. Логарифмічне ди-
ференціювання |
24 |
|
1.6.1 |
Диференціювання функцій, заданих неявно |
24 |
1.6.2 |
Диференціювання функцій, заданих параметрично |
26 |
1.6.3 |
Логарифмічне диференціювання |
28 |
2 |
Диференціал функції та його застосування до наближених обчислень |
....................... 32 |
|
|
2.1 |
Означення диференціала |
32 |
|
2.2 |
Геометричне тлумачення диференціала |
32 |
|
2.3 |
Інваріантність форми диференціала |
32 |
|
2.4 |
Основні правила і формули диференціювання |
33 |
|
2.5 |
Наближені обчислення за допомогою диференціалів |
34 |
3 |
Похідні та диференціали вищих порядків...................................................................... |
38 |
|
4 |
Обчислення границь за правилом Лопіталя................................................................... |
46 |
|
5 |
Асимптоти графіка функції............................................................................................ |
52 |
|
6 Інтервали монотонності і екстремуми функції. Найменше і найбільше значення функції
на відрізку .......................................................................................................................... |
56 |
|
6.1 |
Інтервали зростання і спадання функції |
56 |
6.2 |
Екстемуми функції |
57 |
6.3 |
Дослідження функції на екстремум за допомогою другої похідної |
58 |
6.4 |
Найменше і найбільше значення функції на відрізку |
59 |
7 Опуклість і вгнутість кривої. Точки перегину .............................................................. |
65 |
|
8 Повне дослідження функції і побудова її графіка......................................................... |
69 |
|
9 Застосування похідної в економічній теорії ................................................................. |
74 |
|
Додатки |
.............................................................................................................................. |
76 |
Додаток 1 |
76 |
|
Додаток 2 |
84 |
|
Додаток 3 |
89 |
|
Додаток 4 |
93 |
|
Додаток 5 |
104 |
|
Додаток 6 |
108 |
|
Література ........................................................................................................................ |
109 |
|
2
1. Похідна та її застосування
1.Означення похідної, її геометричне та механічне тлумачення
1.1.1. Означення похідної
Нехай функція y f x визначена в деякому околі точки x0 |
і нехай x0 |
x |
– точка |
|||||||||||||||||||||
цього околу, x 0. Якщо відношення |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
f x0 |
|
f x0 x f x0 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
||
має границю при x 0, |
то ця границя називається похідною функції |
f x |
в точці |
|||||||||||||||||||||
x0 |
і позначається |
f x0 . Таким чином, |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
f x0 |
lim |
f x0 |
lim |
|
f x0 x f x0 |
, |
|
|
(1) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
x 0 |
x |
|
|
|
x 0 |
x |
|
|
|
||||||||
тобто похідною функції |
f x |
в точці |
x0 |
називається границя відношення (якщо |
||||||||||||||||||||
вона існує) приросту функції |
f x |
|
в точці x0 до приросту аргументу, коли приріст |
|||||||||||||||||||||
аргументу прямує до нуля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Якщо функція |
f x |
в точці |
|
x0 |
має скінченну похідну, то вона називається |
||||||||||||||||||
диференційовною в цій точці. |
|
|
|
|
|
|
|
|
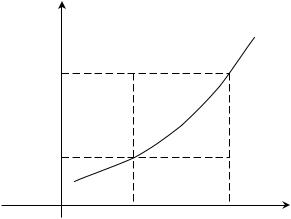
y |
|
y f x |
|||||||||||||
|
Якщо функція |
y f x |
диферен- |
|
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
ційовна в кожній точці інтервалу , то |
|
|
f x x |
|
|
|
||||||||||||||||||
|
|
|
y |
lim |
|
f x x f x |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
f x lim |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
y |
|||||||
|
|
x 0 x |
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
де |
x |
– приріст аргументу; |
y |
– |
f x |
|
|
|
||||||||||||||||
приріст функції (мал.1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||||||||
|
Для того, |
щоб в точці x0 існувала |
|
|
|
|
|
|||||||||||||||||
|
0 |
|
|
x |
x x x |
|||||||||||||||||||
похідна |
функції |
f x , необхідно |
|
і до- |
|
|
|
Мал.1 |
|
|
||||||||||||||
статньо, щоб в цій точці існували права та ліва похідні цієї функції і щоб права похідна дорівнювала лівій, тобто
|
|
f |
x f x |
|
|
|
|
|
|
Якщо |
|
x , то кажуть, що функція |
f x має в точці x нескінченну |
|
f |
||||
похідну. |
|
|
|
|
Для позначення похідної функції y f x |
використовуються й інші символи: |
|||
3

|
|
|
dy |
|
df x |
|
, |
|
, |
|
. |
||
y , |
yx |
dx |
||||
|
|
|
|
dx |
||
Значення похідної при x x0 позначають так:
y x0 , |
f x0 , |
df x0 |
. |
|
|||
|
|
dx |
|
Операція знаходження похідної від даної функції називається диференцію-
ванням цієї функції.
Для безпосереднього знаходження похідної від даної функції y f x засто-
совують наступне загальне правило:
1)надають аргументу x довільний приріст x і знаходять нарощене значення функції y y f x x ;
2) знаходять приріст функції y f x x f x ;
3) складають відношення
y f x x f x ;
x x
4)знаходять границю одержаного відношення при x 0. Ця границя (якщо вона існує) і дає шукану похідну y від функції y f x .
Слід зауважити, що часто у виразі “похідна від функції f x ” слово “від”
опускають і говорять: “похідна функції f x ”.
Розглянемо кілька прикладів.
Приклад 1. Використовуючи означення похідної, знайти похідну функції y 3x2 4x.
Розв’язання. Для даної функції маємо:
1)y y 3 x x 2 4 x x 3x2 6x x 3 x 2 4x 4 x ;
2)y 3x2 6x x 3 x 2 4x 4 x 3x2 4x 6x x 3 x 2 4 x ;
3)y 6x x 3 x 2 4 x 6x 3 x 4;
x x
4)lim y lim 6x 3 x 4 6x 4.
x 0 x x 0
Таким чином, y 6x 4.
Приклад 2. Знайти похідну від функції y sin x при x 0.
Розв’язання. За означенням (1):
|
f 0 x f 0 |
lim |
sin 0 x sin 0 |
lim |
sin x |
1. |
||
|
|
|
|
|
||||
f 0 lim |
x |
x |
x |
|||||
x 0 |
x 0 |
x 0 |
|
|||||
Навіть на простому прикладі (див. приклад 1) видно, що знаходження похідної безпосередньо за означенням забирає багато часу і часто є трудомістким. Тому на практиці питання знаходження похідної розв’язується за допомогою правил і формул диференціювання.
4
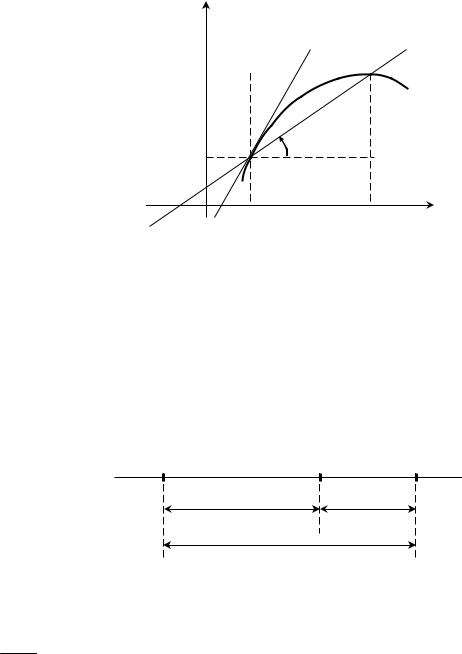
1.1.2. Геометричне тлумачення похідної
Рівність (1) можна записати так:
k tg f x0 , |
(2) |
тобто похідна функції f x в точці x0
кривої y f x в точці x; f x0 з
додатним напрямком осі Ox (мал.2).
Це твердження виражає геометрич-
ний зміст похідної.
Справді, оскільки tg є не-
перервною функцією кута , то
tg tg |
при (мал.2). Отже |
|
кутовий |
коефіцієнт k |
дотичної |
M0T до кривої y f x |
в точці M0 |
|
можна обчислити за формулою
дорівнює тангенсу кута нахилу дотичної до
y
T
f x x 
y f x
y
f x
 x
x
0 |
x |
x x x |
Мал.2
k tg limtg lim |
f x0 x f x0 |
|
lim |
f x0 |
f x0 . |
||
|
|
||||||
|
x 0 |
x |
x 0 |
x |
|
||
1.1.3. Механічне тлумачення похідної |
|
|
|
|
|||
Нехай точка M рухається по прямій за законом S S t , де S |
- довжина шляху, |
||||||
взята від деякої початкової точки |
M0 |
|
M |
M1 |
|||
|
|
|
|||||
M0 ; t - час, за який пройдено
S t
шлях S . Нехай M - положення
точки в момент t (мал.3), M1- в
момент t t; S S t t S t
- довжина шляху, пройденого за час t .
Відношення в механіці називається
відрізку MM1, а границю цього відношення при в точці M , або миттєвою швидкістю в момент момент t позначити через V t , то
середньою швидкістю руху на називають швидкістю руху t. Якщо миттєву швидкість в
V t lim |
S |
|
(3) |
|
|||
|
S t . |
t 0 t
5

Отже переконуємося в тому, що миттєва швидкість в момент t дорівнює похідній від шляху за часом. Це твердження виражає механічний зміст похідної.
1.1.4. Економічний зміст похідної
Будемо розглядати витрати виробництва y як функцію кількості випущеної про дукції x. Нехай x - приріст продукції, тоді y - приріст витрат виробництва а
y середній приріст витрат виробництва на одиницю продукції. Похідна
x
виражає граничні витрати виробництва і характеризує приблизно витрати на виробництво одиниці додаткової продукції.
Граничні витрати залежать рівня виробництва (кількості продукції, що випускається) x і визначаються не постійними витратами, а лише змінними (на сировину, паливо та інше). Аналогічно можно визначити граничний прибуток,
граничний продукт, граничну корисність та інші граничні величини.
Граничні величини характеризують не становище (як сумарна або середня величина), а процес, зміну економічного об’єкту. Таким чином, похідна виступає як швидкість зміни деякого економічного об’єкту (процесу) з часом або відносно іншого фактора, що досліджується. Слід зазначити, що економіка не завжди дозволяє використовувати граничні величини в силу цілості багатьох об’єктів економічних розрахунків і дискретності економічних показників за часом
(наприклад річних, квартальних і т.п.). Але в деяких випадках можна відхилитися від дискретності показників і ефективно використовувати граничні величини.
Для дослідження економічних процесів і розв’язку інших прикладних задач часто використовують поняття еластичності функції.
Означення. Еластичністю функції Ex y називається границя відношення відносного приросту функції y до відносного приросту змінної x при x 0:
|
|
y lim |
|
y |
|
x |
|
|
x |
|
y |
|
x |
y . |
|
E |
x |
|
: |
|
|
lim |
|
||||||||
|
|
|
|
|
|||||||||||
|
|
|
y |
|
x |
|
|
y x 0 x |
y |
||||||
|
|
x 0 |
|
|
|
||||||||||
Еластичність функції показує приблизно, на скільки відсотків зміниться функція y f x при зміні незалежної змінної на 1%.
Властивості еластичності функцій.
1. Еластичність функції дорівнює добутку незалежної змінної на темп зміни функції
|
|
y |
|
|
Ty ln y |
|
|
, тобто Ex |
y x Ty . |
|
||||
|
|
y |
|
|
6
2.Еластичність добутку (частки) двох функцій дорівнює сумі (різниці) еластичностей ціх функцій:
Ex uv Ex u Ex u ,
Ex u Ex u Ex u .
v
Еластичність функції застосовується при аналізі попиту й споживання.
Наприклад, еластичність попиту y відносно вартості x - це коефіцієнт, який
визначається за формулою Ex y |
x |
y і показуєприблизно на скільки відсотків |
|||||||||||||
|
|||||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|||
змінюється попит (об’єм споживання) при зміні вартості на 1%. |
|
|
|
|
|
|
|
|
|
||||||
Якщо еластичність попиту за абсолютною величиною |
|
Ex y |
|
|
1, то попит |
||||||||||
|
|
||||||||||||||
вважають еластичним, якщо |
|
Ex y |
|
1 - нейтральним, |
|
якщо |
|
|
Ex y |
|
1 - |
||||
|
|
|
|
|
|||||||||||
нееластичним відносно вартості. |
|
|
|
|
|
|
|
|
|
||||||
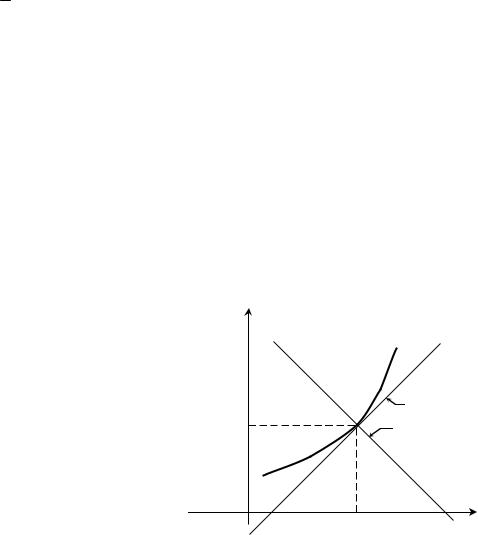
2.Рівняння дотичної і нормалі до кривої
З курсу аналітичної |
геометрії відомо, |
y |
y f x |
|
|
|
|
||
що рівняння прямої, яка проходить че- |
|
|||
|
|
|||
рез точку |
M0 x0; y0 |
з кутовим коефі- |
|
|
цієнтом, |
що дорівнює k , має такий |
f x0 |
дотична Т |
|
вигляд: |
|
|
нормаль N |
|
y f x0 k x x0 .
Дотична |
до |
кривої |
y f x |
в |
|
|
|
|
|
|
точці M0 x0; f x0 |
(мал.4) має кутовий |
0 |
x0 |
|
|
x |
||||
|
Мал.4 |
|
|
|
||||||
коєфіцієнт k |
f x0 . |
Отже, рівняння |
|
|
|
|
||||
|
|
|
|
|
||||||
дотичної буде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
y f x0 f x0 x x0 |
|
|
|
(4) |
|||
Відзначимо, |
що |
коли |
дотична |
паралельна осі |
Ox , то кут |
її нахилу з |
||||
додатнім напрямком осі Ox дорівнює нулю і тоді tg f x0 0. |
|
|
||||||||
Якщо дотична в точці M0 x0; f x0 |
паралельна осі Oy, |
то |
90 |
і тоді |
||||||
tg f x0 . |
|
|
|
|
|
|
|
|
|
|
Пряма, |
яка |
перпендикулярна |
до |
дотичної |
кривої |
y f x в |
точці |
|||
M0 x0; f x0 і проходить через точку |
M0 , |
називається нормаллю до цієї кривоїв |
||||||||
7

точці M0 (мал.4). Оскільки кутові коефіцієнти двох взаємно перпендикулярних прямих на площині зв’язані співвідношенням k1 k2 1, то рівняння нормалі до кривої y f x в точці M0 x0; f x0 набуває вигляду
y f x0 |
1 |
|
x x0 . |
|
(5) |
|
f x0 |
|
|
||||
|
|
|
|
|
||
Зауважимо, що рівняння (5) має сенс за умови |
f x0 0. Якщо ж |
f x0 |
0, |
|||
то рівняння нормалі набуває вигляду x x0 .
Задача. Скласти рівняння дотичної і нормалі до кривої y 5x2 |
3x 2 у точці з абсцисою |
x 1. |
|
Розв’язання. За умовою задачі |
|
x0 1. Тоді |
f x0 f 1 5 12 |
3 1 2 4. |
Знайдемо |
||||||||||||||||||||||||||||||||
похідну функції |
f x 5x2 3x 2 у точці x0 1. Вона дорівнює |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
f 1 x f 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 lim |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
lim |
5 1 x 2 3 1 x 2 5 12 3 1 2 lim 7 5 x 7. |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
x 0 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Згідно з (4) і (5) рівняння шуканої дотичної і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
нормалі мають відповідно вигляд |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
y 4 7 x 1 і |
y 4 |
1 |
x 1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y f2 x |
|
|
|
|
|
|
y f1 x |
|||||||||
або 7x y 3 0 |
і |
x 7y 29 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Кутом |
між |
двома |
кривими |
|
|
y f1 x |
|
|
|
і |
f x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y f2 x у |
точці |
їх |
перетину |
|
M0 x0; y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
називають кут між дотичними до цих кривих |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
в точці |
M0 |
(мал.5), |
який обчислюють |
|
|
за |
|
|
|
0 |
|
|
|
x |
|
|
|
|
|
|
|
|
x |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
формулою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мал.5 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
k k |
|
|
f |
|
x f x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
tg |
|
|
|
|
|
2 |
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
(6) |
||||||||||
|
|
|
|
|
1 k1k2 |
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
1 f1 x0 f |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Задача. Який кут перетину кривих y x2 |
і y2 x? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Розв’язання. Знайдемо точки перетину даних |
ліній. Розв’язуючи систему |
їх |
рівнянь |
||||||||||||||||||||||||||||||||||
y x2 |
одержимо дві точки: |
O 0;0 , |
M 1;1 . Оскільки дотичні до кривих в точці O 0;0 |
||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
y2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 1;1 |
|
|||
збігаються з осями координат, |
то кут між кривими дорівнює 90 . У точці |
кут |
|||||||||||||||||||||||||||||||||||
між кривими визначимо за формулою (6). Враховуючи, що k1 |
y 1 |
|
1 |
|
|
|
|
|
1 |
, |
бо |
||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
дотична до кривої y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
x |
|
x 1 |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
x в точці M утворює з додатнім напрямком осі Ox гострий кут, а |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

k |
|
2, одержимо |
2 y 1 2x x 1 |
|
2 |
1 |
|
3 |
|
|||
|
|
|
|
|||||
|
2 |
|
. |
|||||
tg |
|
|
|
|
|
|
|
|
1 |
|
|
||||||
|
4 |
|
||||||
|
1 2 |
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|||
Отже arctg 3. 4
3.Задача про продуктивність труда
Нехай функція u t виражає кількість виробленої продукції u за час t. Потрібно
знайти продуктивність труда в момент t0 .
За період часу від t0 до t0 t кількість виробленої продукції зміниться від
значення u t0 до u0 |
u u t0 t . Тоді середня продуктивність труда за цей пері |
||||||
од часу zсер |
|
u |
. Продуктивність труда в момент t0 можна визначити як граничне |
||||
|
|||||||
|
|
t |
|
|
|
|
|
значення середньої продуктивності за період часу від t0 до t0 t при t 0, |
|||||||
тобто |
|
|
|
|
|
u |
|
|
|
|
|
z lim zсер |
lim |
. |
|
|
|
|
|
|
|||
|
|
|
|
x 0 |
x 0 t |
||
4.Основні правила диференціювання функцій
|
|
|
|
|
|
|
|
|
|
|
|
C const ; |
(7) |
|||||||||||||
|
C 0 |
|
|
|
||||||||||||||||||||||
|
u v |
|
|
|
|
|
u |
|
v |
|
|
|
(8) |
|||||||||||||
|
w |
|
|
|
w |
; |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
(9) |
|
|
|
|
|
|
uv |
u v uv |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Cu ; |
|
|
|
|
|
|
(9а) |
|||||||
|
|
|
|
|
|
|
Cu |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
u |
|
|
1 |
u ; |
|
|
|
|
(9б) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
C |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
v 0; |
(10) |
|||
|
|
|
|
|
v2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
C |
|
Cv |
, |
|
|
|
|
v 0; |
(10а) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
v2 |
|
|
|
|||||||||||||||||||
|
|
|
v |
|
|
|
|
|
|
|
|
|
df u |
|
du x |
|
|
|||||||||
yx yu |
|
ux |
|
або |
|
dy |
|
|
, |
(11) |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
du |
dx |
|
||||||||
якщо y f u , де u x . Це правило диференціювання складної функції.
Слід пам’ятати, що в наведених правилах C const а y, z, u, v -
диференційовні функції.
9
Таблиця похідних.
|
|
y f x |
|
y f u , |
де u x , |
|
тобто y f x |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nxn 1 |
(12) |
|
|
|
|
|
|
|
nun 1u |
|
|
|
|
|
|
(12а) |
||||||||||||||||||||||||||||||||||||||||
xn |
|
un |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(13) |
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
(13а) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
2 |
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
(14) |
|
|
1 |
|
|
|
|
1 |
|
|
|
u |
|
|
|
|
|
|
(14а) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
x2 |
|
|
u |
|
|
|
|
|
|
|
|
u2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
cosx |
(15) |
|
|
|
|
|
|
|
cosu u |
|
|
|
|
|
(15а) |
|||||||||||||||||||||||||||||||||||||||
sin x |
|
|
sinu |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
sin x |
(16) |
|
|
|
|
|
|
sinu u |
|
|
(16а) |
||||||||||||||||||||||||||||||||||||||||||||
cosx |
|
cosu |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
tgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
cos2 x |
(17) |
|
|
cos2 u u |
|
|
(17а) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
ctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ctgu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
sin2 x |
(18) |
|
|
sin2 u u |
|
(18а) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
ax lna |
(19) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 0, a 1 |
(19а) |
|||||||||||||||||||||||||||||||||||
ax |
au |
au lna u ; |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ex |
(20) |
|
|
|
|
|
|
|
eu u |
|
|
|
|
|
|
(20а) |
|||||||||||||||||||||||||||||||||||||||
|
ex |
|
|
|
eu |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(21) |
|
|
lnu |
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
(21а) |
||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
u |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
loga x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(22) |
loga u |
|
|
|
|
|
|
u ; |
a 0, a 1 |
(22а) |
||||||||||||||||||||||||||||
|
|
|
|
|
xln a |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
arcsin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(23) |
arcsinu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
(23а) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
1 x2 |
|
|
|
|
1 u2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
arccosx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(24) |
arccosu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
(24а) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
1 x2 |
|
|
|
|
1 u2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
arctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctgu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 x2 |
(25) |
|
|
|
|
1 u2 u |
|
(25а) |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
arcctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(26) |
arcctgu |
|
|
|
|
|
|
|
|
|
|
|
u |
|
(26а) |
|||||||||||||||||||||||||||||
|
|
1 x2 |
|
1 u2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ці правила та формули слід запам’ятати і використовувати для знаходження похідних функцій.
Зауваження 1. Починати диференціювання треба із застосування відповідних правил і лише після цього використовувати формули диференціювання основних елементарних функцій (див. таблицю похідних ).
Зауваження 2. Слід мати на увазі, що необов’язково диференціювати задану функцію відразу. Можна попередньо зробити її тотожні перетворення, якщо це доцільно, тобто веде до спрощення диференціювання, а потім продиференціювати.
Зауваження 3. Не рекомендується захоплюватись спрощенням виразів, одержаних
10
