Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный педагогический университет им. М.П. Драгоманова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

diff_calc_econ_ua

.pdf

Скачиваний:

Добавлен:

28.02.2016

Размер:

1.07 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

	ymax	y 1 2 6 18 7 17 ,
	ymin	y 3 54 54 54 7 47.
Приклад 5. Знайти екстремуми функції y x ln 1 x2 .
Розв’язання. Задана функція визначена на всій числовій осі, бо 1 x2							0 для будь-яких x.
Її похідна				1 x 2
y		2x	1 x2 2x
	1	1 x2		1 x2 0
			1 x2
Отже функція зростає, екстремумів немає.
Приклад 6. Знайти найбільше і найменше значення y x4 2x2						5 на відрізку 2;2 .
Розв’язання. Знаходимо y 4x3 4x 4x x2 1 .				Знаходимо		критичні точки першого
роду: y x 0, якщо 4x x2 1 0, звідки x 0, x 1,					x 1 і y x . Відзначимо, що
всі знайдені точки належать відрізку 2;2 .
Обчислимо значення функції в критичних точках і					на кінцях		відрізка: y 2 13,

y 1 4, y 0 5, y 1 4, y 2 13.

Із одержаних значень вибираємо найменше і найбільше: yнм 1 4, yнб 2 13.

Приклад 7. Знайти найбільше і найменше значення y

100 x2

на відрізку 6;8 .

Розв’язання. Діючи, як і в попередньому прикладі, одержимо:

;

100 x2

y 0

при x 0 6;8 ;

y при x 10 6;8 ;

y 6 8, y 0 10, y 8 6

Таким чином,

yнм 8 6,

yнб 0 10.

Приклад 8. Знайти найбільше і найменше значення y x3

3x2 6x 2 на відрізку 1;1 .

Розв’язання. y 3x2

6x 6 3 x2

2x 2 0 при будь-яких

x, оскільки D 4 0,

тому функція

монотонно

зростає

і, отже, y 1 12

- найменше значення функції,

y 1 2 - найбільше значення функції.

Приклад 9. Знайти екстремуми функції y x2 a x 2 , користуючись другою похідною.

Розв’язання. Задана функція визначена для всіх x R. Диференціюючи її двічі, одержимо:

y 2x a x 2 x2 2 a x 1 2x a x a x x

2x a x a 2x 2 a2x 3ax2 2x3 ;

y 2 a2 6ax 6x2 .

Знаходимо стаціонарні точки, тобто точки, в яких похідна y x 0. Розв’язуючи рівняння

2x a x a 2x 0, матимемо

x 0,

,x a.

Обчислюємо

значення

другої

похідної

одержаних

точках:

0 2a

0, y a 2a

іx a функція має мінімум, причому

ymin (0) ymin (a) 0

Таким чином,

в точках x 0

в точці x

- максимум, причому

max

Приклад 10. За допомогою другої похідної знайти екстремуми функції y

всіх x 0;1 1; .

ln x

Розв’язання. Задана функція визначена для

Діючи

далі,

як

попередньому прикладі, одержимо:

ln x x 1 x

ln x 1

ln x 2

ln x 2 ;

y x

1 ln x 2

2ln x

1 ln x 1

ln x ln x 2ln x 2

2 ln x

ln x 4

xln3 x ;

y 0, якщо ln x 1 0, звідки x e - стаціонарна точка.

Обчислюючи значення другої похідної при

x e, маємо:

отже

e;e

y e e

точка мінімуму.

Приклад 11. Виробник реалізує свою продукцію за вартістю p за одиницю,

а витрати при

цьому задаються кубічною залежністю

S x ax x3

a p, 0 . Знайти оптималь-

ний для виробника об’єм випуску продукції й відповідний йому прибуток.

Розв’язання.

Позначимо

об’єм

продукції

Складаємо

функцію прибутку

C x px ax x3 , де px - прибуток від реалізованої продукції.

1)Знаходимо C x p a 3 x2 ;

2)Знаходимо критичні точки:

	2	0,	x1	p a	(другу критичну точку						x2			p a		не розгля-

C x p a 3 x				3										3
даємо за сенсом задачі).				3										3
даємо за сенсом задачі).

3) Знаходимо C x 6 x																p a
			і визначаємо знак другої похідної при x x : C													p a	0,
			і визначаємо знак другої похідної при x x : C													3	0,
													1			3
													1

отже, за другою достатньою умовою екстремуму при x								p a			прибуток максимальний.
отже, за другою достатньою умовою екстремуму при x								3			прибуток максимальний.
								3
									p a
							p a		p a				p a
4) Знаходимо максимальний розмір прибутку C															.
4) Знаходимо максимальний розмір прибутку C															.
						max	3			3		3
							3			3		3

Приклад 12. Капітал у 1 млрд.грн. може бути розміщеним у банку під 50% річних і

вкладеним у виробництво, причому ефективність вкладення очікується в розмірі 100%, а 62

витрати задаються квадратичною залежністю.

Прибуток обкладується податком у

p%.

При яких значеннях

p вкладення в

виробництво є більш ефективним, ніж

чисте

розміщення капіталу в банку?

Розв’язання. Нехай x

(млрд.грн.) інвестується у виробництво, а 1 x - розміщується під

відсотки. Тоді розміщений в банку капітал через рік стає рівним

1 x 1

100

а капітал, вкладений у виробництво

100

2x.

x 1

100

Витрати складають x2 , тобто прибуток від вкладення у виробництво: C 2x x2 .																														p
											2		p															2		p
Податки складають 2x x														, тобто чистий прибуток буде рівним 2x x														1			.
Податки складають 2x x														, тобто чистий прибуток буде рівним 2x x														1	100		.
Загальна сума через рік буде:												100																	100
Загальна сума через рік буде:
								3							p				p		3					p
		A x		3				3	x 2x x2					1		3 2 1					3	x 1					x2 ,
		A x		3			2		x 2x x2					1		3 2 1					2	x 1					x2 ,
				2			2								100	2		100			2				100
і потрібно знайти максимальне значення цієї функції на відрізку 0;1 . Маємо
																						p		3
																				2 1
			p				3						p							2 1	100			2
			p				3						p								100			2
									2 1
																									,
A x 2 1							2						100	x і A x 0 при x0									p		,
			100				2						100										p
																				2 1
																				2 1
																						100
					p																							x0 -
							0,			тобто згідно другої достатньої умови екстремуму																				точка

A x 2 1				100
				100													0;1
максимуму.			Щоб						x0		належала				відрізку		0;1			необхідно					виконання				умови
		p		3						p 25.
0 2 1						1, або
0 2 1	100			2		1, або
	100			2

Таким чином, якщо p 25 краще нічого не вкладати у виробництво а розмістити весь капітал у банку. Якщо p 25, можна показати, що при x x0

						p			3	2
				2 1
			3	2 1		25			2
A x	0		3			25			2		3	A 0 ,
A x								p			3	A 0 ,
		2						p			2
					4 1
					4 1
							100

тобто вкладення в виробництво єкращим, ніж чисте розміщення під відсотки.

Питання для самоперевірки

18.Яка функція називається зростаючою (спадною)?

19.Сформулюйте необхідну і достатню умови зростання (спадання) функції.

20.називають максимумом (мінімумом) функції?

21.Як називають мінімум і максимум функції в точці?

22.В чому полягає необхідна умова існування екстремуму?

23.Сформулюйте достатню умову існування екстремуму.

24.Як називаються точки, в яких похідна дорівнює нулю?

25.Як називаються точки, в яких похідна дорівнює нулю або не існує?

26.Пригадайте правило, за яким знаходяться інтервали монотонності і екстремуми функції.

27.Як досліджується функція на екстремум за допомогою другої похідної?

28.Як знайти найбільше і найменше значення функції на відрізку?

Вправи

Показати, що функція y

x2 1

зростає в будь-якому інтервалі, який не містить точку

x 0.

Знайти інтервали монотонності функції y

Відповідь: в інтервалах 0;1 і 1;e

ln x

функція спадає, а в інтервалі e; зростає.

Знайти інтервали зростання і спадання функції y x cosx .

Відповідь: функція монотонно зростає.

Вказівка. Скористатись тим, що 1 sin x 1.

Знайти екстремуми функції y 2x3 3x2 .

Відповідь: ymax 0 при x 0,

ymin

1 при x 1.

Знайти екстремуми функції y x ln 1 x .

Відповідь: ymin 0 при x 0.

Знайти найбільше і найменше значення функції y x5 5x4

5x3 1 на відрізку 1;2 .

Відповідь: 2 і -10.

Знайти найбільше і найменше значення функції y

x 1

на відрізку 0;4 .

x 1

Відповідь: 3; -1.

зростає в інтервалі 0;1

і спадає в інтервалі 1;2 .

Показати, що функція y

2x x2

Знайти екстремуми функції y x3

2ax2 a2x

a 0

за допомогою другої похідної.

Відповідь: ymax 274 a3 при x a3 , ymin 0 x a.

10. За допомогою другої похідної знайти екстремуми функції y x2e x .

Відповідь: ymax 42 при x 2, ymin 0 x 0. e

7. Опуклість і вгнутість кривої. Точки перегину

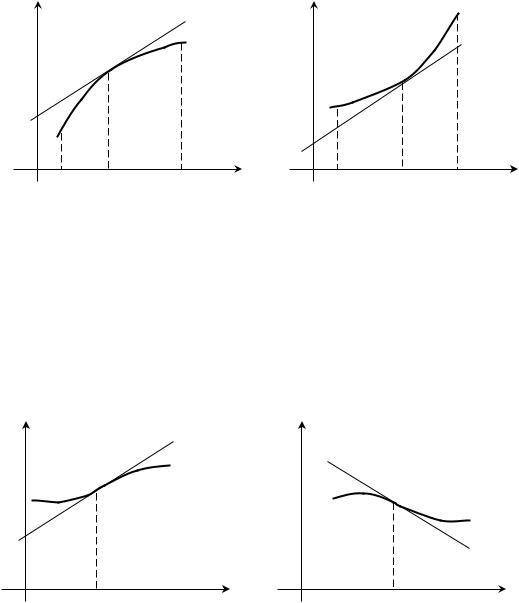
Графік функції y f x називається опуклим (крива обернена опуклістю вгору) на інтервалі a;b , якщо він розміщений нижче дотичної, проведеної в будь-якій точці цього інтервалу (мал.14).

Графік функції y f x називається вгнутим (крива обернена опуклістю вниз) на інтервалі a;b , якщо він розміщений вище дотичної, проведеної в будь-

якій точці цього інтервалу (мал.15).

y f x

0 a		x0	b	x	0	a	x0	b	x
		Мал.14					Мал.15
Якщо ж		x 0 ( f		в	інтервалі	a;b	то графік функції опуклий
Якщо ж	f	x 0 ( f	x 0)	в	інтервалі	a;b	то графік функції опуклий

(вгнутий) в цьому інтервалі. Це є достатня умова опуклості (вгнутості) графіка функції.

Точка x0; f x0 графіка функції, яка відділяє опуклу його частину від

вгнутої, або навпаки, вгнуту його частину від опуклої, називають точкою перегину

(мал.16, а, б).

y	y
y	f x

0	x0	а	x	0	б x0	x
				Мал.16
Якщо	M(x0; y0)	-	точка перегину графіка функції y f x ,			друга похідна
f x0 0 або	f x0 не існує (необхідна умова існування точки перегину).

Точки, в	яких f x0 0 або	f x0	не	існує, називаються критичними
точками другого роду.
Якщо при переході через критичну точку				x0 друга похідна змінює знак, то
точка M(x0; y0)	є точкою перегину	кривої	(достатня умова існування точки

перегину).

Виходячи із цих умов, одержуємо правило для знаходження інтервалів опуклості і вгнутості та точок перегину графіка функції, яке пропонуємо застосовувати на практиці.

8)Знаходимо область визначення функції.

9)Знаходимо f x .

10)Знаходимо f x

	x 0 і точки, де		x не існує (критичні точки
11)Знаходимо корені рівняння f		f

другого роду).

12)Визначаємо знак другої похідної f x в кожному інтервалі, на які знайдені критичні точки розбивають область визначення даної функції, і тим самим знаходимо інтервали опуклості і вгнутості кривої.

13)Визначаємо, які з критичних точок є абсцисами точок перегину (мал.17).

f x	перегин		перегин	?	перегину
f x	перегин		перегин	?	немає
f x	0	–	0		+	0
f x	+	–	+	x3	+	+	x
	x1		x2	x3		x4	x
			Мал.17
Зауважимо, що в точці x3 графік функції f x					має перегин, якщо функція			f x в
цій точці визначена, або немає перегину,				якщо		функція	f x в цій	точці
невизначена;

14)Обчислюємо значення функції в знайдених точках, тобто знаходимо точки перегину графіка цієї функції.

Розв’язання прикладів

Приклад 1. Показати, що графік функції y xarctgx всюди вгнутий.

Розв’язання. Задана функція визначена на всій числовій осі. Знаходимо її першу і другу похідну

			x
	x xarctgx	arctgx	1 x2 ;
y

1 x

x arctgx

1 x2

1 x2 2

1 x2

1 x2 2

1 x2

При будь-яких значеннях x y 0, а це означає, що графік даної функції всюду вгнутий.

Приклад 2. Знайти інтервали опуклості і вгнутості та точки перегину графіка функції y x3 5x2 3x 5.

Розв’язання. 1. Функція визначена для всіх x R.

2.y x x3 5x2 3x 5 3x2 10x 3.

3.y x 3x2 10x 3 6x 10 2 3x 5 .

3x 5 0, звідки

x .

y x 0, якщо

x 3 ;

Для x

x 0, бо, наприклад,

а для x 3

;

x 0,

y 0 10 0,

оскільки,

наприклад,

y 4 14 0

. Отже,

крива є

опуклою, а в

інтервалі ;

інтервалі

35; - вгнутою.

6. В точці x 53 друга похідна даної функції дорівнює нулю і при переході через точку змінює знак, а це означає, що x 53 є абсцисою точки перегину кривої.

7. Обчислюючи значення функції y x3 5x2 3x 5 при x 53 , одержимо y 53 25027

Таким чином, M 53; 25027 - точка перегину графіка даної функції

Приклад 3. Знайти інтервали опуклості і вгнутості та точки перегину графіка функції

y ln 1 x2 .

Розв’язання. Задана функція визначена на всій числовій осі, оскільки 1 x2

для всіх

x R. Диференціюючи її двічі, одержимо:

перегин перегин

;

—

1 x2

21 x2

-1

x 2

1 x2

2x2

2 2 .

Мал.18

1 x

Друга похідна існує на всій числовій осі і обертається на нуль при x 1

і x 1. Ці точки

розбивають область визначення функції на три інтервали ; 1 ,

1;1

і 1;

(мал.18),

в кожному з яких похідна y

x зберігає знак. Визначаючи знак другої похідної в довільно

взятій точці кожного інтервалу, одержимо:

y 2 0,

y 0 0,

y 2 0.

При визначенні знака другої похідної слід врахувати, що знаменник 1 x2 0

при всіх

значеннях x R.

Обчислюючи значення функції y ln 1 x2 при x 1, знаходимо y 1 y 1 ln 2.

Таким чином, графік функції y ln 1 x2 є опуклим в інтервалах ; 1 та 1; і

вгнутим в інтервалі 1;1 . Крива має дві точки перегтну 1;ln 2 і 1;ln2 .

Питання для самоперевірки

29.Яка крива називається опуклою (вгнутою)?

30.В чому полягає достатня умова існування інтервалів опуклості (вгнутості) кривої?

31.Що називається точкою перегину графіка функції?

32.Сформулюйте необхідну і достатню умови існування точки перегину кривої.

Вправи

1.Показати, що графік функції y ln x2 1 всюди опуклий.

2.Знайти інтервали опуклості і вгнутості кривої y xex .

Відповідь: в інтервалі ; 2 крива опукла, а в інтервалі 2; - вгнута.

3. Знайти точки перегину кривої y x 1 7 x 1 6 .

Відповідь: M 1;0 .

4. Знайти інтервали опуклості і вгнутості та точки перегину графіка функції

y x 1 4 ex .

Відповідь: точок перегину немає, графік функції вгнутий.

5. Знайти інтервали опуклості і вгнутості та точки перегину кривої y x4 12ln x 7 .

Відповідь: в інтервалі 0;1 крива опукла, а в інтервалі 1; - вгнута.

Точка перегину 1; 7 .

8. Повне дослідження функції і побудова її графіка

Повне дослідження функції рекомендується проводити за такою схемою:

1.Знайти область визначення функції.

2.Встановити точки розриву та інтервали неперервності функції.

3.Дослідити функцію на парність та непарність.

4.Знайти точки перетину графіка функції з осями координат.

5.Знайти інтервали знакосталості функції.

6.Знайти асимптоти. Дослідити поведінку функції поблизу точок розриву.

7.Знахйти інтервали зростання і спадання функції та екстремуми.

8.Знайти інтервали опуклості і вгнутості графіка функції та точки перегину.

9.Побудувати графік функції за результатами дослідження.

Зробимо кілька зауважень щодо цієї схеми.

15)Якщо функція виявиться парною або непарною, то дослідження досить провести лише для невід’ємних значень аргументу, а потім скористатись властивістю симетрії.

16)Якщо в результаті дослідження виявиться, що функція періодична, то наступне дослідження цієї функції досить провести на відрізку довжиною в період.

З’ясувавши всі особливості функції на цьому відрізку, встановлюємо (внаслідок періодичності) її особливості в усій області існування.

17)Доцільно наносити на малюнок характерні точки, асимптоти і т.п. паралельно з дослідженням. Це скоротить роботу з накресленням графіка.

18)Щоб якмога точніше накреслити графік функції в тих інтервалах області її існування, в яких немає особливостей цієї функції і які великі за розмірами, треба взяти кілька точок і обчислити значення функції в цих точках.

Розв’язання прикладів

Приклад 1. Провести повне дослідження функції y e x x.

Розв’язання. Задана функція визначена на всій числовій осі, крім точки x 0. Отже, в ін-

тервалах ;0 і 0; функція неперервна, а x 0 - точка розриву функції. Функція не ні парною ні непарною, бо y x e 1x x y x і y x y x . Отже вона несиметрич-

на. Функція неперіодична. Графік функції не перетонає вісь Oy, бо	x 0. Розв’язуючи
рівняння y x 0, знаходимо точки перетину графіка з віссю Ox : e	1	1
	x x 0,	e x x,

1x ln x ; звідки x 1.5 (мал.19). Таким чином, графік функціїпроходить через точку 1.5;0 .

Знаходимо інтервали знакосталості функції (мал.20): y 0 при x 1.5; y при x 0;

y 1 e 1 1 0;

y 1 e 1 0;

y 2 e

2 0.

y ln x

y +

∞

–

1.5

Мал.20

з дослідження,

робимо висновок: для

Виходячи

1.5

x ;0 0;1.5

графік

функції

розміщений

Мал.19

вище осі Ox , бо для цих x

y 0, а для x 1.5;

графік функції розміщений нижче осі

Ox , бо для

цих x y 0. Далі досліджуємо функцію поблизу точок розриву і знаходимо асимптоти.

Як відзначалося вище, x 0 - точка розриву функції. Знаходимо

;

lim y lim e

e 0

x 0

lim

y lim

x x

x 0

Отже, x 0 – вертикальна асимптота функції при x 0.

Тепер знаходимо похилі асимптоти y kx b, де

1 1,

lim

x x

lim y kx lim

x x

lim

x e

e x

Таким чином, y x 1 - похила асимптота.

Оскільки y e

1 e

1 0

для

всіх

із області визначення, то

функція монотонно спадає, а тому екстремумів немає.

Знаходимо інтервали опуклості і вгнутості та точки перегину:

2xe

1 2x

;

y 0, якщо 1 2x 0,	звідки x	1	;	y при x 0.

	2

Зауважимо, що при визначенні знака y x (мал.21)
слід враховувати, що e	1
	x 0 і x4 0 для всіх значень

x із області визначення функції.

			точка
y	перегин		розриву
y	+	0	+ ∞	+
		-0.5	0	x

Мал.21

	2	y 1 0, y 14 0, y 1 0			2
			крива є опуклою, а для			;0	0; - вгнутою.
Таким чином, для x ;	1			x	1
yперегину e 2 0.5 0.6 при				x 0.5.

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.02.2016739.34 Кб5Confucianism.pdf
#
04.09.2019114.19 Кб2Cоц. опитування -соціологія політики.docx
#
28.02.2016757.61 Кб4Daoism.pdf
#
28.02.20161.87 Mб446Davnya_ukr_lit_Metodichka_2009.doc
#
04.09.201977.24 Кб14default.docx
#
28.02.20161.07 Mб6diff_calc_econ_ua.pdf
#
28.02.2016122.25 Кб5dilova.docx
#
28.02.2016750.08 Кб17Diplomna_Onischuk_Ivan_Viktorovich_Word.doc
#
28.02.201661.66 Кб28Doc1.docx
#
28.02.201658.87 Кб17Doc1.docx
#
18.12.2018203.26 Кб0dohodi.doc