38.Вычисление теоретич.Частот для норм.Распр-ния.

Пусть имеется выборка(х₁,…х_n)объема n,и есть основание предпол., что она имеет норм.распр.Вычислим теорет. частоты:1)По данным выборки построить интерв. вариац. ряд.Для этого весь инт-л наблюд.знач.Х надо разделить на k частичн. инт-ов(х_i,x_i+1)одинак. длины. Находим х_min, x_maxи размах варьирования R=x_max-х_min.Для опр-ния количества инт-ов групп-ки k воспольз. форм.Стерджеса: k=3,32*lgn+1.Число k округл-ся в сторону наиб.целого числа.Тогда находим ширину частичн. инт-ов(х_i,x_i+1): h=R/k. Необх. чтобых_minи x_max входили внутрь инт-ов.Для этого в качестве левой границы 1^го инт-ла можно взять числох₀=х_min-h/2,а в качестве правой границы посл. интер.х_k+1=x_max+h/2.В качестве частоты n_i вариац. ряда запис. число наблюд.,попавших в кажд. [x_i,x_i+1)промеж.; 2)Для оценки параметров МО а и средн.квадр.отклонения σ перейдем к дискр.ряду,взяв в качестве вариант ряда Х середины построен.интер.x_i^*.В итоге получим послед-ность равностоящ. вариант и соответств.им частот.Несмещенной оценкой МО явл. выборочн.среднее x_В,а дисп. -исправленная выборочн.дисп.S² .

а=x_В=1/n*∑x_i*n_i,σ²=S²=1/n-1*∑(x_i*- x_В)²*n_{i или}S²=(n/(n-1))*Dв.

3)Сделаем преобразов.стандартизации для Х,перейдя к велич. и ,.Причем наим.знач. z₀=-∞, а наиб. знач. z_k+1=+∞,т.к.теор.норм.распред.приним.знач.на всей числовой оси. 4)Вычисл.вер-сти p_iпопадания Хв инт-лы(z_i,z_i+1) p_i=P(z_i<x<z_i+1)=Ф₀(z_i+1)-Ф₀(z_i),где i=0, k,Ф₀(х)-ф-ция Лапласа; 5)Рассчитаем теор.частоты n_i’=np_i.

Замеч.:1.чтобы эмпир.ф-ция распр-ния лучше описывала теор-кую,нужно,чтобы число инт-лов было по возможности большим.;2.для выполнения предельного перехода к распред.χ²нужно,чтобы n_i>5.Если какой-то инт-л содер.малые знач. n_i,то он объед-тся с соседним инт-лом,а их частоты склад-ся.Тогда число степ.свободы критерия χ² уменьш.на 1.

39. Сравнение дисперсий двух нормальных выборок.

Пусть выборки X и Y распределены нормально с параметрами а₁ и ₁ ; а_{2 , 2}соответсвенно: X~N(а₁,₁), Y~N(а₂,₂).

Гип.H₀ будет справедл.,если будут равны пар-рыа₁=а₂;₁=₂

Сравним сначала дисперсии этих выборок. H₀: ²₁=²₂

Несмещенной и состоятельной оценкой дисперсии явл. исправленная выборочная дисперсия.

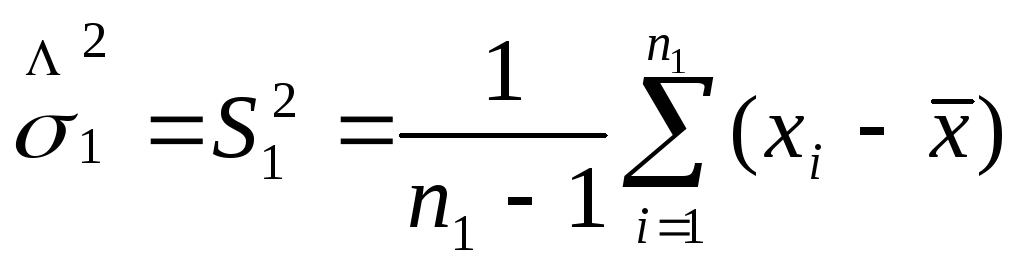
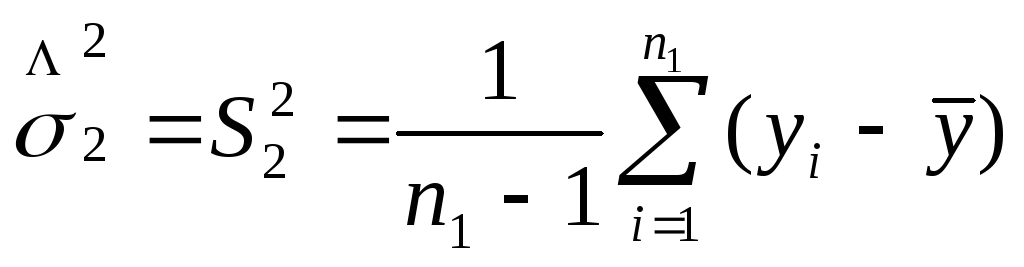
Сравнение дисп-й всегда осущ.путем вычисл.их онош.F=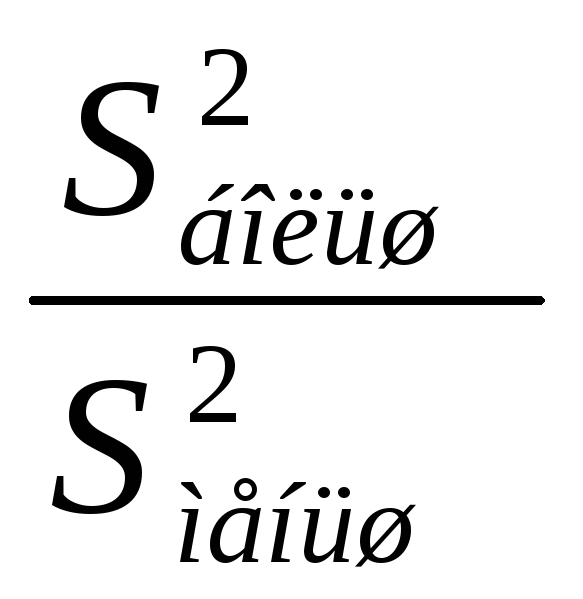

Можно показать,что при H₀ эта СВ имеет распред.Фишера с k₁ и k₂ числом степ.свободы. F=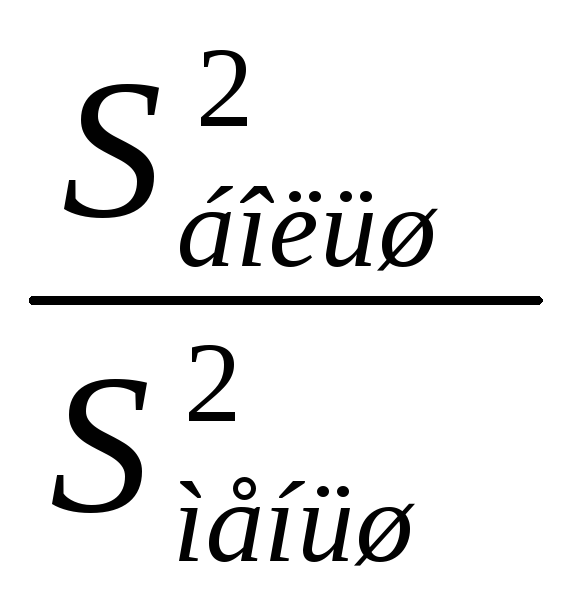~F(k₁,k₂). Причем k₁=n₁-1, k₂=n₂-1, S²_1>S²₂

1. Пусть H1:S²_1>S²₂, т.е.правостор.критич.область.F_k(K_кр)=1-

Проверка H₀ осуществляется сл.образом:

– Вычисляется наблюдаемое значение критерия.F_набл=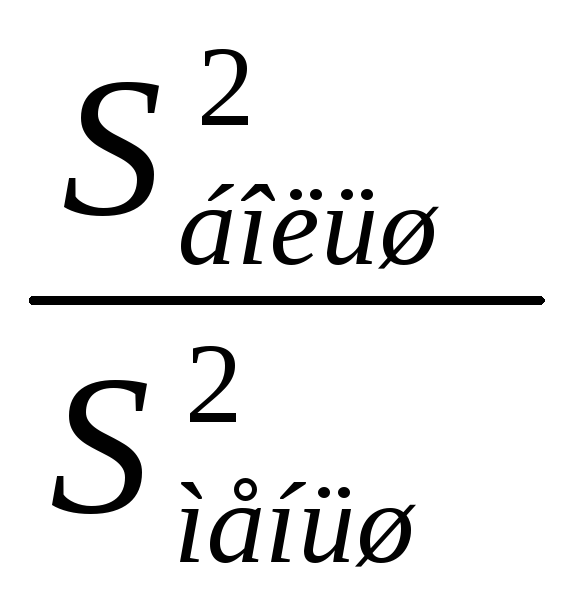

– Выбирается уровень значимости и по таблице крит.точек распред.Фишера находятF_кр(,k₁,k₂)

– Если F_набл>F_{кр ,}то H₀ отвергаем и приним.конкурирующую.

2. Пусть H1: S²₁S²₂ -двусторонняя критическая область.

В этом случае поступают аналогично, только F_кр(/2,k₁,k₂)

Замеч.:Критерий Фишера примен в предположении нормальн. распред.,а норм.распред.может состовлять выборка с объемом не<30.

40.Сравнение средних 2х норм.Выборок(Крит.Стьюдента)

Пусть имеется2выборки с объемами n₁и n₂,распред-е по норм. з-ну. X~N(а₁,₁),Y~N(а₂,₂)Проверим гип.H₀ о рав-ве МО. H₀: a₁=a₂; H₁: a₁a_2. Несмещенной состоятельной оценкой МО- выборочн.средняя.H₀:.Поэтому H₀ можно сформ-вать,что средние равны..Средние сравнив.путем вычисления их разности и построения СВT=, )-ошибка разности средних. _,

_где

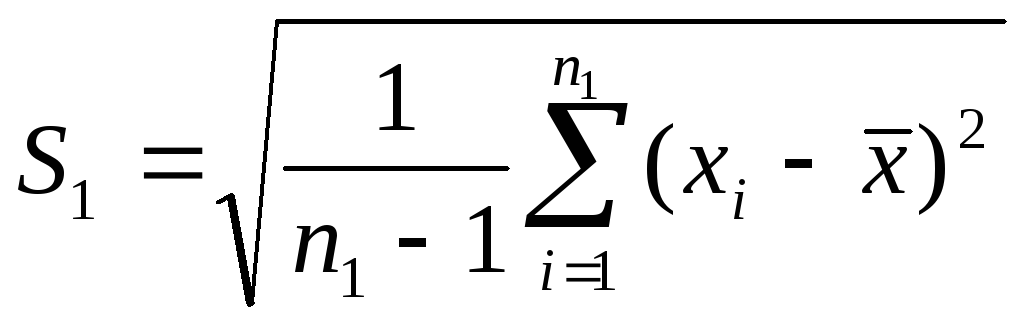
1. S₁=S₂,можно показать,чтоТ~T(n₁+n₂-2).

Проверка H₀ осущ.сл.обр.Вычисляем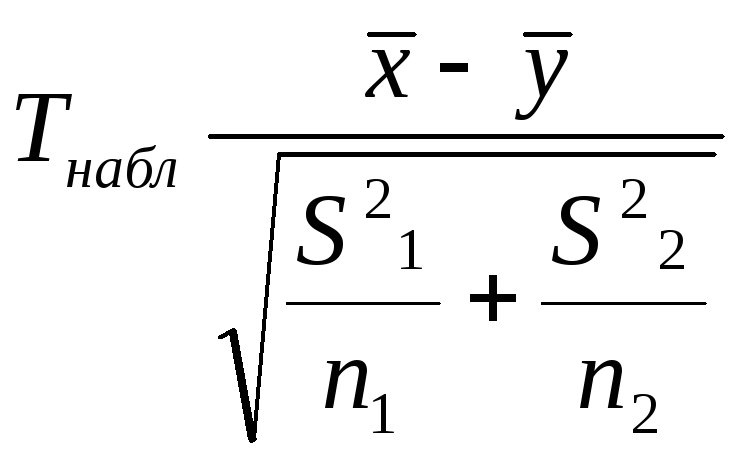

По табл.крит.точек распр.Стьюд.находимТ_кр=(,n₁+n₂-2),-выбран.ур.значимости.If |T_набл|<|T_кр|,нет оснований отвергн. H₀→средние различаются недостоверно(случайно). If |T_н|>|T_кр|, H₀ отвергаем и прин.H₁→средние различ.достоверно.

2. S₁≠S₂.В этом случае о распред.СВничего нельзя сказать. Можно лишь гов.о том,что n₁,n₂→∞эта величина→к распред. Стьюд.с числом степ.свободы

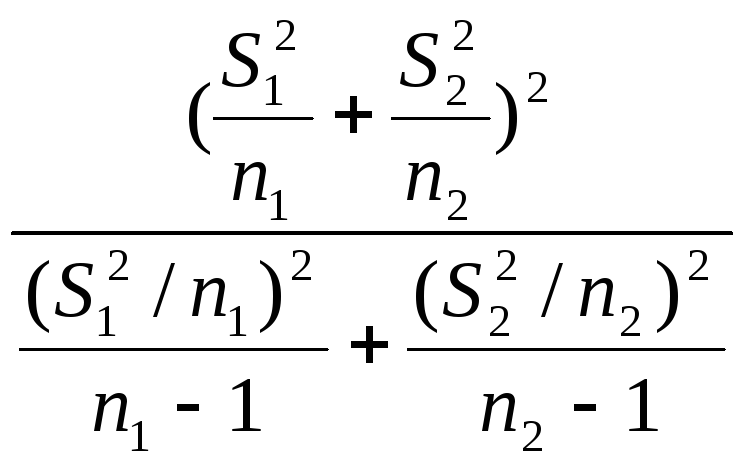
Замечание:Крит.Стьюд. можно исп-ть, если Т_набл намного >Т_кр.