6. Формула полной вер-сти. Ф-ла Байеса.

Пусть событие А может произойти только с одним из n несовместных событий H₁…H_n, образующих полную группу:

Ø,,тогда.

По правилу сложения вер-тей несовм.соб.получаем . А по правилу умноженияP(H_iA)=P(H_i)P(A/H_i). Откуда оканчательно имеем - формулу полной вероятности.

События H₁, H₂,…, H_n часто называют гипотезами.

Иногда интересует, как перераспределятся вероятности гипотез после того, как событие А уже произошло: . По теореме умножения , .

Подставляя в знаменатель формулу полной вероятности, получим формулу Байеса:

.

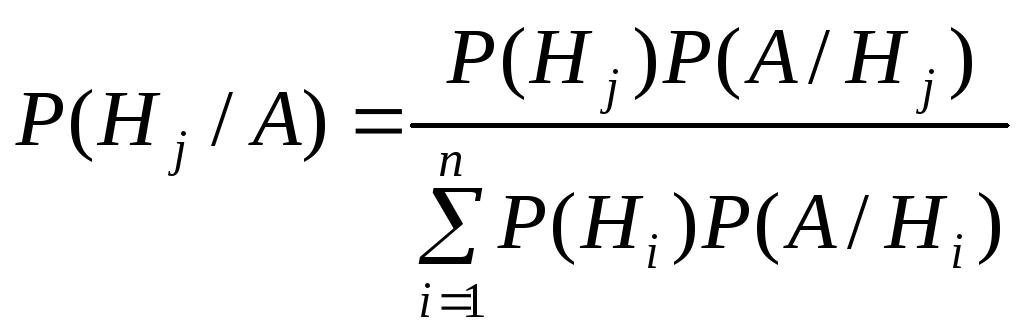7. Схема независимых испытаний Бернулли

Пусть производится n независ.испытаний, в каждом из кот.может появ.соб.А или не появится.Вер-сть появления соб., не появления , .

Под элементарн.событием в схеме Бернулли поним.послед-сть наступлений и не наступл.соб.А в n испытаниях.

Требуется найти вероятностьP_n(m) того, что соб.А в этих n опытах появиться ровно m раз.

Для произвольных m и n вероятность одного элементарного исхода равна p^mq^n-m . Число таких элементарных исходов равно числу способов разместить m единиц по n местам, а это по определению есть число сочетаний из n элементов по m. Получим формулу Бернулли .

Часто в схеме Бернулли интересует вероятность появления события А не ровно m раз, а от m₁ до m₂ раз включительно. Тогда она определяется формулой:

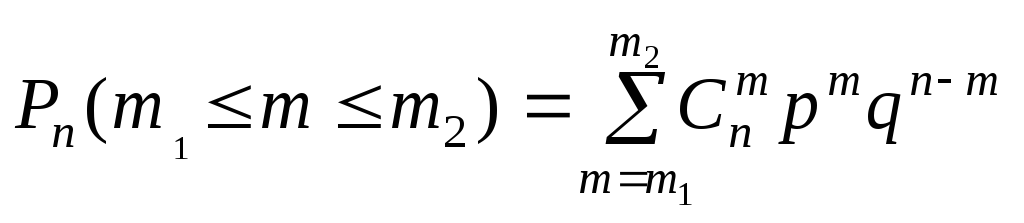
8. Предельные теоремы в схеме Бернулли.

При больших n применение форм.Берн.затрудн-но из-за сложности выч.факториалов и степеней.В этом случ.исп-тся приближ.формулы.Рассм.2 случая: 1)или;

2) p(0,1)и не близко ни к 0, ни к 1.

Теорема Пуассона. If в сх.Берн., так,что np a, тогда .Замеч.:1)–среднее число появл.соб.А вn испыт-ях.2как правило,теор.Пуассона прим,когда 3)В конце книг поТВесть табл.для подсчета вер-ти для разл.aи m.

Лок.предельная теорема Муавра-Лапласа.If вер-сть наступл. некот.соб.в n независ.испыт.постоянна и=p,p(0,1),то вер-сть того,что в этих испыт.соб.A наступ.ровноmраз, удовл.при n соотнош.,гдеравном-но по всемm, для кот.наход. в каком-то конечн. интервале; Ф-ция -плотность норм.распред.

Интегр.пред.теорема Муавра-Лапласа.If m-число наступл. соб.в n независ.испыт.,в каждом из кот-х вер-сть этого соб.=p, p(0,1),то равномерно относ-но a и b (−∞<a<b<+∞) n имеет место соотношени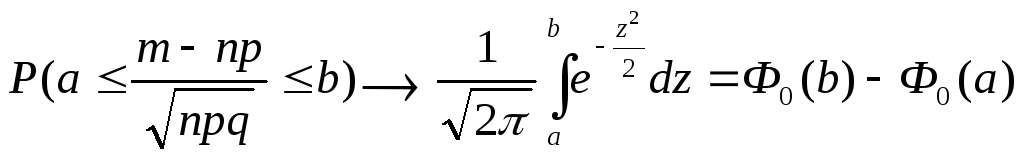е , где 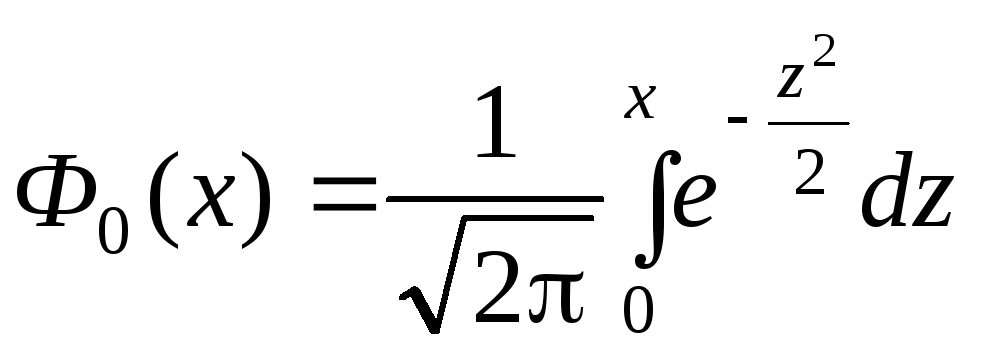-ф-ция Лапласа. Замеч.:1)Ф-ция Лапласа нечетная:= -.2)Ф₀(z) асимптотич-я и приона быстро стрем.к 0,5. Это стремл. настолько быстрое, что при можно счит=0,5. 3) Плотность норм.распред. - четная функция.4)Ф-ции , в конце книг по ТВиМС заданы таблично.

9. Функция распределения вероятности и ее свойства.

Случ.велич.ξ, наз.величина, значеие кот.завис.от случая. Функция определенная на множестве элемент-х событий Ω.СВобознач.греч. буквами, напр.ξ(кси), η(эта) и т.д.,а их возможные значения малыми лат.буквами x₁,x₂,...,y₁,y₂… СВ бывают дискретные (если приним.конечное или счётное знач.), недискретные и др. Законом распред.дискретной СВ ξ наз. соответствие между возможными знач.и их вер-ми. Обычно для дискр. СВ ξ закон распред. изображ.в виде табл. Соб.ξ= x₁;ξ=x_2,… несовместны и образуют полную группу, поэтому ∑p_i=1

Пусть ξ-СВ и x -произвольное действит.число.Вер-сть того, чтопримет знач.меньшее чем x наз.функцией распред. вер-ти..СВ наз.непрерывной, если ее ф-ция распред.F(x)непрерывна.

Функция распределения вероятностей явл. неслуч. функциикй, вычисленной на основ.закона распределения СВ.

Свойства функции распределения:

1. , 0 , так как это вероятность.

2. F(x) –неубывающая функция.т.е.

Следств:2.1) Вер-сть попаданияСВ в задан.интервал есть приращ.ф-ции распред.на этом интервале.P(x₁≤≤x₂)=F(x₂)- F(x₁).

2.2)Вер-сть принять одно фиксиров.знач.для непрерывной СВ=0,т.к. функция распред.непрерывной СВнепрерывна.

2.3) Вер-сть попадания непрер.СВ в откр.или замкнутый промеж. одинакова. P(a≤≤b)= P(a<≤b)= P(a≤<b)= P(a<<b).

3. F(x)непрерывна слева в кажд.точке

4.F(-∞)=0

5. F(+∞)=1