10. Плотность распределения вероятностей и ее свойства.
Плотностью
распределения
вер-тей СВ
наз.производная
функции распределения:
.
Свойства.
1.
,
,
т.к.это производная неубыв.функции.
2.
,
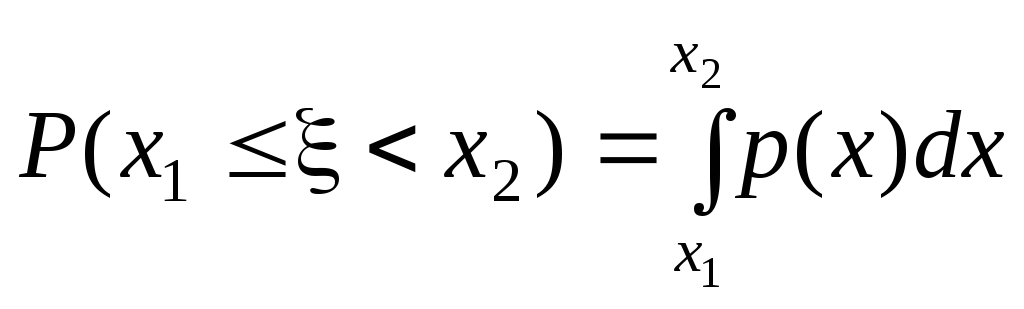т.к.
3.
.Следует
из определения и свойства 2.
4.
Свойство нормировки:
.
В
частности,если все возможные значения
СВ заключены в интервале от a
до b,
то
.
СВ наз.распределенной по равномерному закону, если ее плотность вер-ти принимает постоянное значение в пределах заданного интервала.
11.Математическое ожидание и его свойства.
Мат.ожиданием
дискретной СВ
наз.сумма произведений всевозможных
её значений на вероятности этих значений
=
,если
этот ряд сходится абсолютно.If
мат.ожид.(МО)=бесконечности,то гов., что
оно не существует.МО хар-ет среднее
знач.СВ,взвешенное по вероятности.
МО
непрерывной СВ
с плотностью вероятностей p(x)
назыв-ся.интеграл
=
,
если он сходится абсолютно.
Свойства МО:
1. MC=C;
2.
МО суммы СВ равно сумме их МО: M(
)=M
+M
;
3.
Для независимых СВ
и
МО
произведения равно произведению МО:
M(
)=M
*
M
.
Следствие:
постоянный множитель выносится за знак
МО: М(a*
)=a*M(
).
12. Дисперсия и её свойства.
Дисперсией
наз.мат.ожидание квадрата отклонения
СВ ξ от своего мат.ожидания: 
.
Выполним преобразования:
Для дискретн.СВξ с з-ном распред.(xi,pi) дисперсия равна
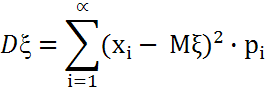или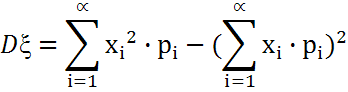
Для
непрерывной
СВ ξ с плотностью вер-ти p(x)
дисперсия равна
,
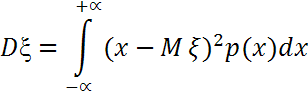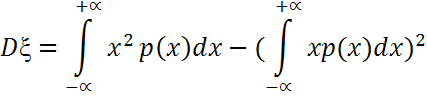
Дисперсия
характ.рассеяние возможных знач-й ξ
вокруг своего МО. Средним
квадрат.отклон.-корень
квадратн.из дисперсии
.
Свойства дисп.:
1) =0.DC=M(C-MC)2=M(C-C)2=0
2)Для
независ.СВ дисп.сумы= суме дисп-й:
3)Если
a
и b
= const,
то
Следствие
Постоянный множитель выносится за знак дисп.в квадрате
.
13.Коэффициент корреляции и ковариация
К числов.хар-кам связи относ.ковариацию, коэфф.корр-ции.
Ковариацией
СВ
1,
2
-МО
произведения отклонений СВ от своих
МО.
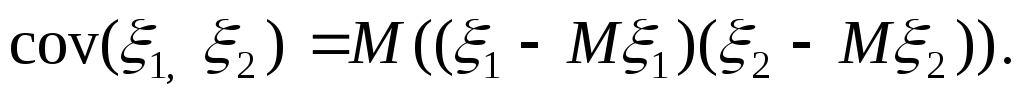Свойства
ковариации:
1.
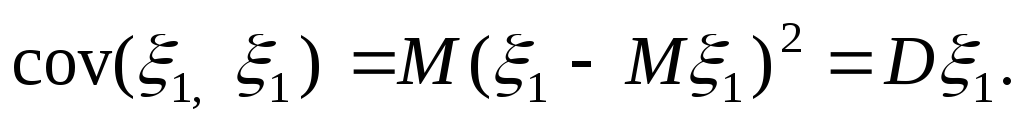
2. Для независимых СВ ковариация =0. Обратное не верно.
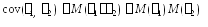
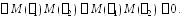
3. Пост.множитель выносится за знак ков-ции.
4.
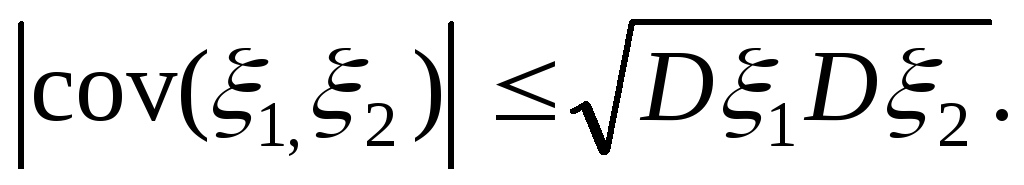
Ковариация служит для качеств.хар-ки зависимости м/у СВ.
Коэфф.корреляции
наз.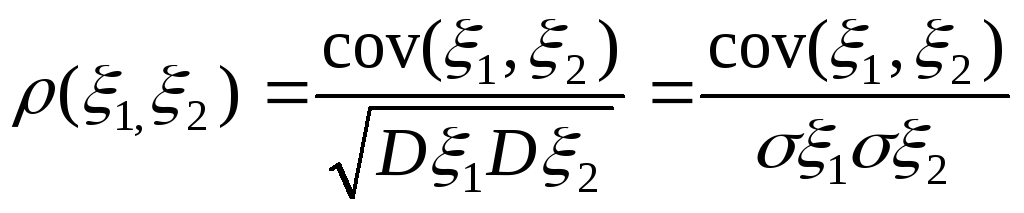
.
Свойства
коэфф.корреляции:1.
.
2.
Если
и
независимы, то коэфф.корреляции = 0.
Обратное не верно, если p=0
– некоррелированны.
3.
Если
1
и
2
связаны линейной зависимостью
,
то
Причем, если
то
;
если
,
то
.
Если
,
то говорят, что
1
и
2
связаны
корреляционной зависимостью, тем более
тесной, чем ближе
к 1.
Коэффициент корреляции служит для количественной характеристики меры линейной зависимости случайных величин.
14. Моменты
МО и дисперсия явл.частными случаями моментов СВ.
Начальным мом.порядка k СВ X наз-тся МО k-й степени этой величины. α k = М(Xk )
Для дискр. СВ x нач.мом.:α k =∑ хik*pi , а для непрер. СВ:
α k =∫ х k * f (х) dх. α=MX, α2=MX2
Центральным
мом.порядка
k СВ
наз.МО в степениk
отклонения СВ от своего МО. µ
k
= М(
– М
)k
В
частности , µ
2
= D
, т.е. центр.мом.2го пор.-дисперсия;
µ
1
= М(
– М
)
=0
Любой центр.мом.можно выразить ч/з нач. мом. µk=f(υ1,…,υk)
15. Основные дискретные распределения св.
1.
Биноминальное распределение.
Рассмотрим схему Бернулли. Производится
послед-ность n независ.испытаний в каждом
из кот-х возможно только 2 исхода:соб.А
появ.с вер-ю p:
P(A)=p, и не появ с вер-ю q:P(
)=q.
p+q=1
Число
появлений соб.А в серии из n незав.испыт.может
принимать знач.
Вер-сть
этих знач.вычисл.по форм.Берн.
Найдем МО: Mµi =0*q+1*p=p; Mµ =np
Чтобы найти дисперсию: Mµ 2=02*q+12*p=p
Dµ = Mµ2 -(Mµ)2=p-p2=p(1-p)=pq
Так как дисперсии независимы Dµ =npq
2.
Распределение Пуассона-наз.распределение
вер-тей дискр.СВξ, определяемое формулой
P(
=m)=P(m)=
m=0,1,...,n ; где а-параметр распределения Пуассона.
,
,
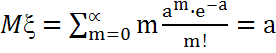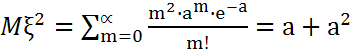тогда D
=а
В распределении Пуассона МО и Дисперсия =а
3. Геометрическое распределение - наз.распределение дискр.СВξ, определяемое формулой Pm=qm-1p
M
=1/p;
D
=
.