
ЦСУ_Егоров
.pdf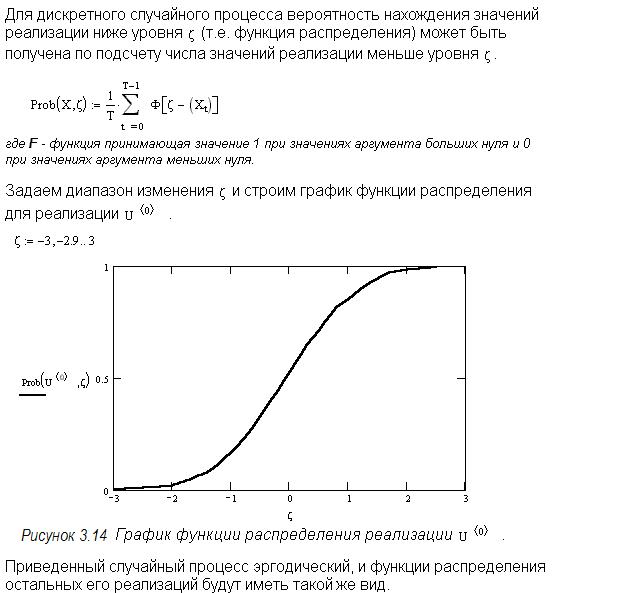
3.7Свойства функции распределения
1.Вероятность того, что случайная величина примет значение на полуинтервале (a,b), где a<b, равна разности значений функции распреде- ления на концах этого интервала.
Pr ob[ a ≤ x( t1 ) ≤ b ] = Pr ob( b ) − Pr ob( a ). |
(3.33) |
Рассмотрим случайное событие А = [x(t1)< b], заключающееся в том, что случайная величина x(t1) примет значение меньше b. Очевидно, что это событие представлено как объединение двух непересекающихся событий x(t1)³a и x(t1)<b, или
[x(t1 ) ≤ b] = [a < x(t 1 )] + [x(t1 ) ≤ b] . |
(3.34) |
42
Тогда на основании принципа сложения вероятностей имеем
Prob[x(t1 ) ≤ b] = Prob[a < x(t1 )] + Prob[a < x(t1 ) ≤ b], |
(3.35) |
Prob[a < x(t1 ) ≤ b] = Prob[x(t1 ) ≤ b] - Prob[a < x(t1 )]. |
(3.36) |
|
2. Функция распределения Р(х) стремиться к нулю при неограничен- ном уменьшении ξ и стремится к единице при неограниченном возраста- нии ξ
lim P( x ) = 0 , lim P( x ) = 1. |
(3.37) |
|
ξ →−∞ |
ξ →∞ |
|
В самом деле при x → −∞ случайное событие x(t) становится не- возможным, так как случайная величина не может принимать значения меньше чем − ∞ . С другой стороны случайное событие x(t)< ∞ является достоверным.
3.8 Плотность распределения
Если функция распределения вероятности случайной величины Р(х) x(t) дифференцируема, то всегда можно взять ее производную
p( x ) = |
dP( x ) |
. |
(3.38) |
|
|
||
|
dx |
|
|
Плотность от функции распределения есть предел отношения того, что случайная величина примет значение внутри интервала x(t1) + x(t1) к длине этого интервала. Или, что тоже самое – плотность распределения определяет вероятность того, что значения процесса в произвольный мо- мент времени будут заключены в определенном интервале.
Рассмотрим некоторую реализацию как функцию времени (рис. 3.15)
k
и вычислим отношение временного интервала T[x(t) x] = ∑ ti нахож-
i =1
дения функции в указанном диапазоне к общему времени наблюдения этой функции T. Определим вероятность нахождения случайной величины в указанном диапазоне
Pr ob[x(t ) |
x] = lim |
T[x(t) |
x ] |
(3.39) |
||
|
|
|
. |
|||
T |
|
|||||
|
T →∞ |
|
|
|
||
Плотность распределения |
|
|
|
|||
p(x) = lim |
Pr ob[x(t) x ] |
|
|
(3.40) |
||
|
|
|
|
|
|
|
x |
|
|
|
|||
x →0 |
|
|
|
|||
Таким образом плотность распределения определяет скорость изме- нения функции распределения. Поэтому вероятность различных событий можно находить интегрированием плотности распределения вычисляя площадь под графиком р(х).
43

Рисунок 3.15 Определение плотности распределения вероятности по одной реализации
3.9Свойства плотности распределения вероятности
1.Вероятность того, что значения случайного процесса заключенно- го между х1 и х2 равна
x2
Pr ob[ x1 ≤ x( t ) ≤ x2 ] = ∫ p( x )dx = Pr ob( x2 ) − Pr ob( x1 ). |
(3.41) |
x1 |
|
2. Интеграл от плотности распределения вероятностей по всей чис- |
|
ловой оси равен 1 |
|
∞ |
|
∫ p( x )dx = 1 . |
(3.42) |
−∞ |
|
Площадь всей области, ограниченной графиком плотности вероятно- сти, равна 1, а значения случайного процесса в любой момент времени бу- дет заключено между − ∞ и ∞ .
3.10 Нормальный (гауссовский) шум
Плотности распределения большого числа случайных процессов, описывающих физические явления, хорошо аппроксимируются выражени- ем вида:
p(x) = |
1 |
|
e −( x − μ ) |
2 |
/ 2σ |
2 |
|
|
|
|
|
|
. |
(3.43) |
|||
|
|
|
|
|
||||
σ 2π |
|
|
||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
где μ1 и σ соответственно среднее значение и среднеквадратичное откло- нение.
Функция (3.43) впервые была получена в 1733 г. и обычно называет- ся нормальной, или гауссовской, плотностью. Для удобства обычно табу- лируется и графически изображается плотность нормированной случайной величины
44
z = (x − μ ) / σ |
(3.44) |
с нулевым средним и единичным среднеквадратичным отклонением. Этим простым преобразованием выражение (3.43) приводится к виду
p( x ) = |
1 |
|
e− z |
2 |
/ 2 . |
|
||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
(3.45) |
|||||
|
|
|
|
|
|
|
||||||
σ |
2π |
|
||||||||||
|
|
|
|
|
|
|
||||||
Нормированное нормальное распределение имеет вид |
||||||||||||
|
|
1 |
|
|
∞ |
2 |
|
|
|
(3.46) |
||
P(z) = |
|
|
|
|
|
e−z |
/ 2dz . |
|
||||
|
|
|
|
|
|
|||||||
|
|
|
2π |
|
|
−∞∫ |
|
|
|
|
|
|
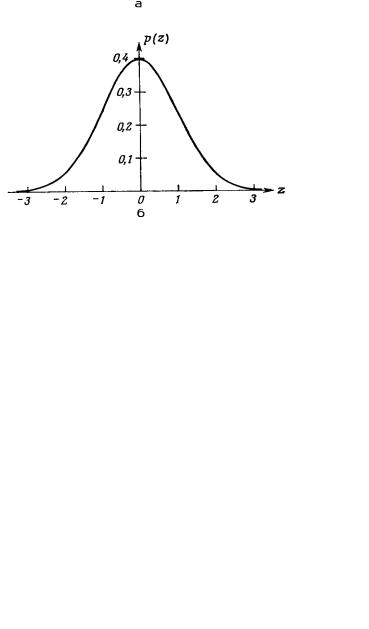
Графики функций нормированного нормального распределения и его плотности приведены на рисунке 3.16.
Рисунок 3.16 Нормированная гауссовская функция распределения и ее плотность;
а– функция распределения; б– плотность распределения
Важность нормального распределения определяется применимостью на практике центральной предельной теоремы теории вероятностей, кото- рая не строго формулируется следующим образом: если случайная вели- чина х есть сумма п статистически независимых случайных величин
45

x1,x2,¼,xn с произвольными плотностями распределения, то плотность распределения x1,x2,¼,xn приближается к нормальной плотности, если п стремится к бесконечности. Случайные явления очень часто действительно являются результатом взаимодействия многих независимых случайных факторов, поэтому нормальное распределение часто служит хорошей ап- проксимацией плотностей случайных процессов.
По двум причинам желательно предполагать, что случайные процес- сы имеют нормальное распределение.
Во-первых, как следует из формулы (3.45), нормальное распределе- ние полностью определяется двумя параметрами – средним значением μ и
среднеквадратичным отклонением σ . Поэтому для определения нормаль- ной плотности достаточно оценить только эти два параметра процесса. Во- вторых, все линейные операции над нормально распределенными случай- ными величинами приводят к нормально распределенной случайной вели- чине. Это значит, что различные линейные операции, встречающиеся в ма- тематике, такие, как преобразование Фурье и интегрирование, выполняе- мые над нормально распределенными случайными величинами, дают в ре- зультате нормально распределенные величины.
46
3.11 Числовые характеристики (моменты) случайной величины
Расчеты, выполненные с использованием функций распределения вероятностей или плотности распределения, громоздки и сложны. Стати- стические свойства случайных величин могут быть описаны на основе числовых характеристик.
Одной из наиболее важных числовых характеристик случайной ве- личины является ее среднее значение, называемое также математическим ожиданием.
Математическим ожиданием М[x] случайной величины x(t) называ- ется число, определяемое интегралом вида
∞ |
|
М[x] = μ = ∫ x( t1 )p( x )dx , |
(3.47) |
−∞ |
|
где р(х) – плотность распределения случайной величины; х(t1) – воз- можные ее значения заданные ансамблем реализаций в момент времени t1.
Моменты стационарного случайного процесса х(t), описывающего некоторое интересующее нас событие определяются следующим образом
∞ |
(3.48) |
М[xк]= μк= ∫ x k ( t1 )p( x )dx , |
k = 0 ,1,2.... |
−∞
Первый момент называется математическим ожиданием или средним значением.
Второй момент называется средним квадратом
47

∞ |
(3.49) |
М[x2] = ∫ x 2 ( t1 )p( x )dx .
−∞
Положительный квадратный корень из среднего квадрата процесса называется среднеквадратичным значением процесса.
Второй и высшие моменты, вычисленные относительно среднего значения, называются центральными моментами.
Второй центральный момент называется дисперсией
∞ |
(3.50) |
σ 2 = ∫ |
(x(t1 ) − μ) 2 p(x)dx . |
−∞
Положительный квадратный корень из дисперсии называется сред- неквадратичным отклонением
|
∞ |
|
(3.51) |
σ = ∫(x(t1 ) − μ) 2 p(x)dx . |
|
||
|
−∞ |
|
|
|
3.12 Оценивание средних значений |
|
|
Математическое ожидание, средний квадрат и дисперсия, задавае- мые соответственно формулами (3.49), (3.50), (3.51), могут быть определе- ны и непосредственным усреднением реализаций случайного процесса х(t).
Если обратиться снова к ансамблю реализации, то в общем нестаци- онарном случае среднее значение в фиксированный момент t1 определяет- ся следующим образом
μ (t1 ) = lim |
1 |
N |
(t1 ). |
|
|
∑xi |
(3.52) |
||||
|
|||||
N →∞ |
N i=1 |
|
|
||
Аналогично средний квадрат находится как среднее квадратов зна- чений реализации в фиксированный момент t1 по всему ансамблю
|
1 |
|
N |
(3.53) |
||
μ2 (t1 ) = lim |
|
∑ xi2 (t1 ). |
|
|||
|
|
|
||||
N →∞ |
|
N i =1 |
|
|||
Вычисление дисперсии |
|
|||||
|
|
1 |
N |
(3.54) |
||
σ 2 (t1 ) = lim |
∑{xi (t1 )− μ1 |
(t1 )}2 . |
||||
|
||||||
N →∞ N i =1 |
|
|||||
В частном случае стационарных эргодических непрерывных процес- |
||||||
сов моменты разного типа не зависят от времени и могут быть вычислены по единственной реализации х(t) по формулам:
|
1 |
|
T |
|
|
||
μ1 = lim |
|
∫ x(t )dt , |
(3.55) |
||||
|
|
||||||
T →∞ T |
0 |
|
|
||||
μ2 = lim |
1 |
|
T |
(t )dt , |
|
||
|
∫ x2 |
(3.56) |
|||||
|
|
||||||
T →∞ T |
0 |
|
|
||||
48

T
σ 2 = lim 1 ∫{x(t )− μ1}2 dt , (3.57)
T →∞ T 0
В случае дискретных случайных стационарных эргодических про- цессов (отсчеты производятся в дискретные моменты времени) оценки числовых характеристик можно найти также по одной реализации:
Среднее значениеμ1 |
= lim |
1 |
N |
(3.58) |
||||
∑ xi , |
|
|||||||
|
|
|
||||||
|
|
N →∞ N i =1 |
(3.59) |
|||||
Средний квадрат μ1 = lim |
1 |
|
N |
|||||
∑ xi2 , |
|
|||||||
|
|
|||||||
|
|
N →∞ N i =1 |
(3.60) |
|||||
|
|
1 |
N |
|||||
Дисперсия σ 2 = lim |
|
∑( xi − μ1 )2 |
, |
|||||
|
|
|||||||
N →∞ N i =1 |
(3.61) |
|||||||
Среднеквадратичное отклонение |
||||||||
N
σ = lim ∑( xi − μ1 )2 ,
N →∞ i =1
где i-номер отсчета случайной величины.
Приведенные формулы содержат операцию перехода к пределу, ко- торая на практике не осуществима, поскольку нельзя обработать бесконеч- ное число реализаций или одну реализацию бесконечной длины.
3.13 Корреляционные функции и спектральные плотности
Случайный процесс считается полностью заданным если известны его все n-мерные функции распределения. Однако экспериментальное определение даже двумерных функций, равно как и основанные на них расчеты, оказываются слишком сложными и громоздкими. Общую зави- симость значений процесса в некоторый момент времени от значений в другой момент времени можно получить с помощью автокорреляционной функции.
Прежде чем рассмотреть автокорреляционную функцию рассмотрим классическое понятие корреляции. Широкий круг инженерных приложе- ний теории случайных процессов связан с выявлением линейных зависи- мостей между двумя или более совокупностями данных.
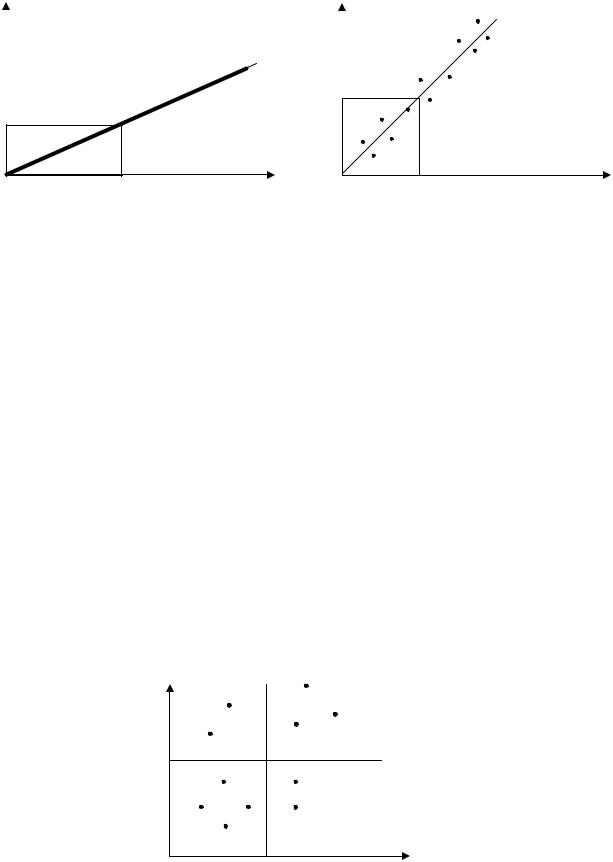
Пусть в некотором эксперименте получены два множества результа- тов измерений xi i = 1,2,…n; и yi i = 1,2,…n. Например входной и выход- ной сигналы усилителей постоянного тока. xі-входное напряжение, yі – выходное напряжение. В идеальном случае проведенные измерения дают идеальную линейную характеристику для рис.3.18 а
49
Y Y
µу
µу
µх |
а) X |
µх |
б) X |
Рисунок 3.18 Различные степени корреляции.
а - точная линейная корреляция, б - умеренная линейная корреляция.
Тогда сразу можно записать уравнение
y = а + bх (3.62)
где a – значение линейной функции при х = 0; b – наклон прямой.
Однако при более точных исследованиях напряжений исследуемая зависимость может оказаться не совсем идеальной прямой. Тогда мы по- лучим результаты экспериментов, изображенные на рис.3.18 б, где угады- вается линейная связь между хі и уі .
Меру линейности связи х у можно задавать с помощью корреляции
|
|
1 |
N |
|
|
σ xy |
= lim |
∑(xi − μx )( yi − μ y ) . |
(3.63) |
||
|
|||||
|
|
N i=1 |
|
||
|
N →∞ |
|
|||
Если хi и уi не связаны между собой как на рис. 3.19, то сумма полу- |
|||||
ченных |
положительных произведений (xi − μ x ) и ( yi − μ y ) |
равна |
|||
сумме отрицательных значений этих произведений и усредненное значе- ние σ xy = 0
Y
μ1
μ1 |
X |
Рисунок 3.19 Отсутствие корреляции
В случае представленном на рис.3.19, xi- μx u yi- μy одновременно ли- бо положительны, либо отрицательны и их усредненное произведение все-
50
гда положительно σху= σх σу. В качестве меры корреляции обычно берут отношение, которое называется коэффициентом корреляции.
ρху=σху/ σх σу, -1≤ρху≤1. |
(3.64) |
Автокорреляционная функция
Автокорреляционная функция случайного процесса характеризует общую зависимость значений процесса в некоторый данный момент вре- мени от значений в другой момент. Рассмотрим реализацию x(t) приведен-
ную на рис. 3.20
x(t) |
t |
|
t
T
Рисунок 3.20 определение автокорреляционной функции
Оценку величины автокорреляционной функции, связывающей зна- чения х(t) в момент времени t u t+t можно получить, вычисляя среднее произведение этих ординат и усредняя произведения в пределах времени наблюдения Т. Найденное среднее значение произведений, приближается к точному значению автокорреляционной функции при стремлении Т к бес- конечности:
R x (τ ) = |
1 |
T |
x ( t ) x ( t + τ )dt . |
|
|
lim |
|
∫ |
(3.65) |
||
|
|||||
|
T → ∞ T |
|
|
||
|
|
|
0 |
|
|
Величина Rx(t) – |
всегда действительная, четная функция с максиму- |
||||
мом в точке t=0 Rx(0)³ Rx(t) .
Найдем автокорреляционную функцию для периодического детер- минированного сигнала
x(t ) = a sin(ωt + ϕ ) |
(3.66) |
понимая при этом под термином корреляционная функция просто резуль- тат применения к функции х (t) операции, выражаемой интегралом (3.65).
Имеем
51
