
ЦСУ_Егоров
.pdf6 ОБРАБОТКА СИГНАЛОВ, ПРЕДСТАВЛЕННЫХ ЧИСЛОВЫМИ ПОСЛЕДОВАТЕЛЬНОСТЯМИ
6.1 Типовые воздействия
Высокое быстродействие современных вычислительных машин позволяет реализовывать регуляторы в системах автоматического управ- ления с П-, ПИ-, ПИД- законами регулирования. При этом основные поло- жения классической теории автоматического управления могут быть при- менены для цифровых систем. Однако обработка информации в цифровом коде накладывает свои особенности на математическое описание цифро- вых систем управления.
Рассмотрим математическое описание цифровых систем управле- ния применяемое для расчетов регуляторов и их моделирования.
По принципу своего действия промышленный контроллер (регуля- тор в цифровых системах автоматического управления) является устрой- ством дискретного действия. В цифровых системах на вход могут пода- ваться непрерывные и дискретные сигналы. Решетчатая функция, как мо- дель дискретного сигнала, может формироваться из непрерывной функции либо из любой числовой последовательности некоторой величины, опре- делённой в равноотстоящие моменты времени. Рассмотрим некоторые важные решетчатые функции, используемые при анализе цифровых АСУ и цифровых систем обработки информации.
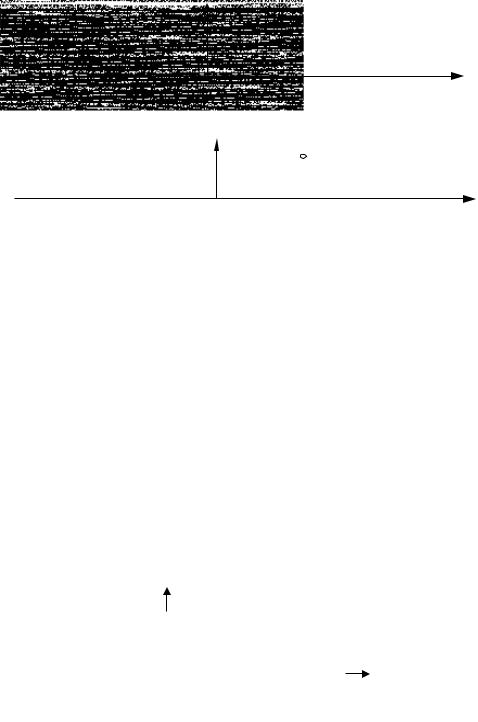
Цифровой единичный импульс (рис. 6.1 а).
1 [n] = 1, |
при n = 0 |
(6.1) |
|
|
|||
0 |
0, при n ¹ 0 |
|
|
Цифровой единичный импульс задержанный на
мер, n0 = 2 (рис.6.1, б). |
|
||||
|
|
|
|
1, при n = n |
o |
1 |
|
[n − n |
|
|
|
|
|
] = |
|
||
|
0 |
|
0 |
0, при n ¹ n |
|
|
|
|
|
|
o |
n0 отсчетов, напри-
(6.2)
102
а) |
|
|
10[n] |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-3 |
|
-2 |
|
-1 |
|
0 |
|
1 |
|
2 |
|
3 |
|
|
n |
||
б) |
10 |
[n − n0 |
] |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
n |
|||||||||
Рисунок 6.1 Цифровой единичный импульс
В дискретных системах этот импульс играет такую же роль, как единичный импульс (дельта - функция Дирака) в аналоговых системах. Важное различие между ними заключается в том, что цифровой единич- ный импульс является физически реализуемым сигналом, а аналоговый - обобщающей функцией.
Единичный скачок 1[n] (рис. 6.2) задаётся следующим образом
1[n]= 1, при n ³ 0 |
|
|
0, при n < 0 |
|
|
Единичный скачок связан с единичным импульсом соотношением |
||
1[n] = |
∞ |
|
∑10[n−m]. |
(6.6) |
|
|
m=o |
|
1[n]
n
Рисунок 6.2. Цифровой единичный скачок. Следующей важной последовательностью является синусоидальная
(рис. 6.3).
x[n] = А× sin(ωnT + ϕ ) n = 0,1... , |
(6.7) |
где A- амплитуда, ϕ - начальная фаза. |
|
103
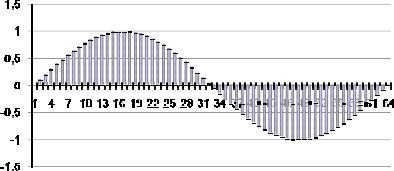
x[n]
nT с
Рисунок 6.3. Дискретная синусоида x[nT ] = Asin(ωnT + ϕ )
Синусоидальная последовательность может быть заменена симво- лической записью в комплексном виде
x[n] = e j(ωnT +ϕ ). |
(6.8) |
Символичность записи заключается в том, что на самом деле дис- кретная синусоида определяется мнимой частью приведенной комплекс- ной функции.
Произвольная последовательность может быть легко выражена с использованием единичного импульса.
Рассмотрим числовую последовательность a[0], a[1], a[2]...a[n],
где а[ n] - значение n-го элемента. Такая последовательность опи- сывается равенством:
∞ |
a[m]10 |
(6.9) |
a[n] = ∑ |
[n − m]. |
|
m = −∞ |
|
|
В равенстве (6.9) используется задержка единичного импульса на m отсчётов и масштабирование его умножением на множитель a[ m] .
6.2 Применение преобразования Лапласа для анализа дискретных функций времени
Эффективный математический метод описания дискретных функ- ций основывается на замене последовательности импульсов х[nT] на ре- шетчатую функцию, состоящую из идеальных импульсов. Такая решетча- тая функция физически не реализуема, она служит лишь удобной формой представления реальных импульсов.
Будем считать, что преобразование непрерывного сигнала в реаль- ный дискретный можно реализовать с помощью схемы (рис. 6.4).
104
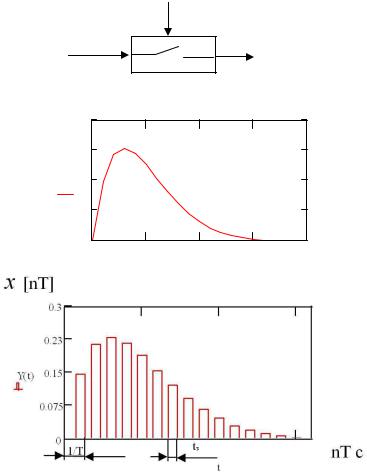
Если период замыкания и размыкания ключа Т значительно боль- ший чем продолжительность времени положения ключа в замкнутом со- стоянии tз, то дискретная последовательность х[nT], имеющая площадь x[nT]tз можно приближенно заменить идеальными импульсами δ (t) той
же площади.
|
|
Т |
|
|
|
x (t) |
|
|
|
x [nT] |
|
x (t) |
|
a) |
|
|
|
0.3 |
|
|
|
|
|
|
|
|
|
|
|
|
0.23 |
|
|
|
|
Yt() |
0.15 |
|
|
|
|
|
0.075 |
|
|
|
|
|
0 |
0.5 |
1 |
1.5 |
2 |
|
0 |
||||
|
|
|
t |
|
|
|
|
|
б) |
|
|
г)
Рисунок 6.4. Преобразование непрерывного сигнала в реальный дискретный а) n; б) непрерывный сигнал; г) реальный сигнал.
Последовательность идеальных импульсов описывается выражением:
∞ |
|
x[δ (t)] = ∑x[nT ]δ (t − nT ) |
(6.10) |
n=0 |
x [nT] и |
В дальнейшем будем считать, что последовательности |
|
x [δ (t)]примерно равны |
|
x [nT] ≈ x[δ (t − nT )] . |
(6.11) |
Преобразование Лапласа заключается в том, что функция веще- ственной переменной x (t) преобразуется в функцию F(p) комплексной пе- ременной p = a + jω . Исходная функция называется оригиналом, а пре-
образованная – изображением.
105
F ( p) = L{f (t)}= ∞∫ f (t)e− pt dt |
|
(6.12) |
|
0 |
|
|
|
Применение преобразования Лапласа к единичному импульсу дает |
|||
L{δ (t)}= ∞∫δ (t)e− pt dt = 1 , |
|
(6.13) |
|
0 |
|
|
|
а применение этого преобразования к импульсу, сдвинутому на nT |
|||
тактов дает |
|
|
|
L{δ (t − nT )}= ∞∫δ (t − nT )e− pt dt . |
|
(6.14) |
|
0 |
|
|
|
Введем новую переменную λ = t − nT , тогда t = λ + nT . С уче- |
|||
том принятых обозначений выражение (6.14) примет вид |
|
||
∞ |
|
∞ |
|
L{δ (t − nT}= ∫δ (λ)e− pλ e−nT dλ = e− pnT ∫δ (λ)e− pλ dλ = e− pnT |
(6.15) |
||
0 |
|
0 |
|
С учетом допущения соотношений преобразование Лапласа реаль- |
|||
ной дискретной последовательности приобретает вид |
|
||
∞ |
|
|
|
L{x[nT ]}= ∑x[nT ]e− pnT . |
|
(6.16) |
|
n=0 |
|
|
|
Такое преобразование называется дискретным преобразованием |
|||
Лапласа. |
|
|
|
Обозначив Z(p) = e pt |
получим Z-преобразование |
|
|
∞ |
|
|
|
Z{X [nT ]}= ∑x[nT ]z |
−n . |
|
(6.17) |
n=0
6.3Математические модели линейных цифровых систем
Цифровая система (звено), с точки зрения её математического опи- сания, по существу является преобразованием входной последовательно- сти в выходную в соответствии с заданным алгоритмом. Обозначим вход- ную последовательность через x[n], а выходную через y[n]. Если на вход
системы подать некоторые входные последовательности x1[n], x 2 [n]...x n [n], то на выходе будут некоторые выходные последова-
тельности соответственно y1[n], y 2 [n]...y m [n], которые называются откли-
ками системы.
Линейной называется такая система, у которой при подаче на вход суммы двух и более последовательностей x1[n]+ x2[n], на выходе образу-
ется последовательность y1[n]+ y2[n], .
106
Система с постоянными параметрами характеризуется тем, что ес- ли входной последовательности x[n]соответствует выходная последова-
тельность y[n], то выходной последовательности x n - n 0 при любых n0 ,
соответствует последовательность y[n − n0 ].
Связь между входными величинами и выходными в цифровых си- стемах можно определить с помощью разностных уравнений.
В разностных уравнениях аналогом первой производной является либо первая прямая разность:
Dy[n] = y[n + 1] - y[n], |
(6.18) |
либо первая обратная разность |
|
Ñy[n] = y[n] - y[n - 1]. |
(6.19) |
Прямая разность определяется в момент времени t = nT по буду- щему значению решетчатой функции при t = (n + 1)T . Это можно сделать,
если будущее значение известно (числовая последовательность выборок сигнала на каком-то интервале времени записана в память машины), либо если это будущее значение можно вычислить по аналитическим зависимо- стям.
Обратная разность определяется |
для момента времени |
tn = nT по |
прошлому значению решетчатой |
функции в момент |
времени |
tn−1 = (n −1)T . |
|
|
Аналогом второй производной непрерывной функции служат вто- рые разности прямая
D2 y[n] = Dy[n + 1] - Dy[n] = y[n + 2] - 2y[n + 1] + y[n], |
(6.20) |
и обратная |
|
Ñ2 y[n] = Ñy[n] - Ñy[n - 1] = y[n] - 2y[n - 1] + y[n - 2]. |
(6.21) |
Аналогично приведенным формулам могут вычисляться высшие прямые и обратные разности.
Аналогом интеграла непрерывной функции в пределах выборки от 0 до n для решетчатой функции является неполная сумма
107
n−1 |
(6.22) |
y[n] = ∑y[m].
m=0
иполная сумма
n |
(6.23) |
y[n] = ∑y[m]
m=0
Отличие выражений (6.22) и (6.23) состоит в том, что значение y[ n] при определении полной суммы также участвует в формировании ре-
зультата.
Динамические непрерывные объекты описываются дифференци- альными уравнениями, дискретные - разностными. Для однозначного ре- шения дифференциального уравнения необходимо знать начальные или конечные условия. Если система описывается уравнениями n-го порядка, необходимо знать n-1 начальных или конечных условий. В большинстве задач анализа систем управления начальные условия задаются в момент времени t=0.
Чаще всего математическое описание системы представляется раз- ностными уравнениями с обратными разностями. Однако есть класс задач, например, вариационные, когда задаются конечные условия в конечный момент времени и возникает необходимость решения задачи в обратном времени. В этом случае в разностных уравнениях используется прямая разность и обратное время.
При использовании обратных разностей линейные неоднородные уравнения имеют вид:
amÑm y[n]+ am−1Ñm−1 y[n]+ ... + a0 y[n] = x[n], |
(6.24) |
где х[n] - заданная, а y[n] - искомая решётчатая функции. При x[n] = 0 уравнение становится однородным.
Разностные уравнения легко решаются на цифровых машинах по известному значению функции в правой части уравнения и начальным условиям.
Так разностные уравнения первого порядка самого общего вида
y[n] = a1 y[n −1]+ b0 x[n]+ b1x[n −1], |
(6.25) |
можно реализовать с помощью схемы, изображенной на рис 6.5
108
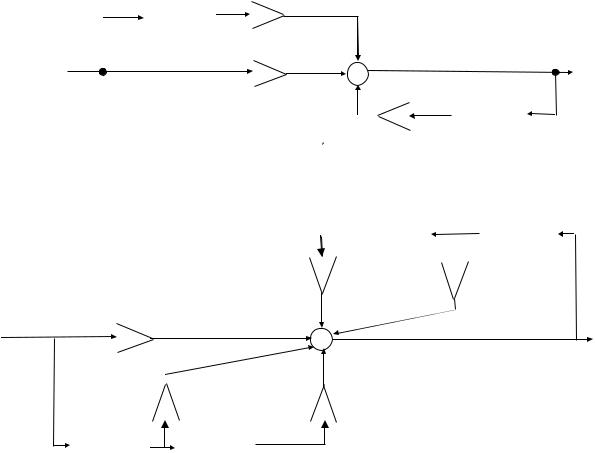
Блок задержки, на этой схеме, реализованный программным путём, осуществляет задержку на один отсчёт. Аналогично может быт решено разностное уравнение второго порядка (рис 6.8).
y [n ] = − a1 y [n − 1]− a 2 y [n − 2 ]+ b0 x [n ]+ b1 x [n − 1]+ |
|
+ b 2 x [n − 2 ]. |
(6.26) |
|
|
|
|
|
|
|
|
|
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задержка |
|
|
|
+ |
|
|
|
|
|
|
|
|
y[n] |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x[n] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
b0 |
y[n-1] |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
-a1 |
|
|
|
|
Задержка |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Рисунок 6.5 Схема решения на цифровой машине разностного |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
уравнения первого порядка |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y[n-2] |
|
|
|
|
|
|
|
Задержка |
|
|
|
|
Задержка |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
b0 |
|
|
|
|
|
|
|
|
|
-a2 |
|
|
y[n-1] |
|
|
-a1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Х[n] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y[n] |
||||
|
|
|
b1 |
|
|
|
Х[n-1] |
|
b2 |
|
|
|
|
|
|
Х[n-2] |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задержка |
|
|
|
Задержка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 6.6 Cхема решения на цифровой машине разностного уравнения второго порядка
Для примера рассмотрим решение разностного уравнения первого порядка.
a1Ñy[n]+ a0 y[n] = b x[n]. |
(6.27) |
|
|
0 |
|
В записанном разностном уравнении перейдём к дискретам |
|
a1(y[n]− y[n − 1]) + ao y[n] = box[n], |
(6.28) |
|
|
y[n]×(a1 + ao ) = -a1y[n -1]+ box[n] и окончательно |
|
109
y[n] = −ry[n−1] + qx[n], |
|
|
(6.29) |
||||
где |
r = |
|
a1 |
, q = |
|
bo |
. |
|
|
|
|||||
|
+ ao |
a1 |
|||||
|
|
a1 |
|
+ ao |
|||
В качестве входной последовательности x[n]возьмём единичный скачок и примем нулевые начальные условия: y[n − 1] = 0 . На (рис. 6.7)
приведена огибающая решетчатой функций полученной в результате ре- шения разностного уравнения.
Системы, входом и выходом которых служат решётчатые функции, описываются уравнениями в конечных разностях. Эти уравнения также иногда удобно представлять по аналогии с непрерывными, преобра- зованными в функции комплексной переменной. В этом случае основой служит дискретное преобразование Лапласа или Z-преобразование.
Пусть дано разностное уравнение
aoy[n]+ aoy[n −1]+ ... + ay[n − m] = box[n]+ b1x[n −1]+ ... + bnx[n − 2] (6.30)
Выполним Z-преобразования этого уравнения. Воспользовавшись известной теоремой Z-преобразования о изображении запаздывающей на k тактов решетчатой функции
|
F (z){f |
[n − kn]}= Z −knF (z), в результате получим |
|
|
||||
ao + a z |
−1 + ... + a mz |
−m Y(z) = |
bo + b z−1 |
+ ... + bn z−n |
X(z) . |
(6.31) |
||
|
1 |
|
|
|
1 |
|
|
|
По аналогии с непрерывными системами для дискретных систем вводится передаточная функция, как отношение изображения выходной переменной Y(Z) к входной X(Z) при нулевых начальных условиях.
Передаточная функция будет иметь вид:
|
b |
o |
+ b z−1 + ... + b |
r |
z−n |
(6.32) |
||||||
W(Z) = |
|
|
1 |
|
|
|
|
. |
|
|||
a |
o |
+ a z |
−1 |
+ ... + a |
m |
z−m |
|
|||||
|
|
|
1 |
|
|
|
|
|
||||
Умножив числитель и знаменатель выражения (6.36) на Z m получим выражение передаточной функции с положительными степенями числите- ля и знаменателя:
|
b |
o |
zm + b zm−1 |
+ ... + b |
zm−n |
|
||||
W(Z) = |
|
|
|
1 |
r |
|
|
. |
(6.33) |
|
|
a |
|
zm + a zm−1 + ... + a |
|
||||||
|
|
o |
m |
|
||||||
|
|
|
|
1 |
|
|
|
|||
Этой передаточной функции соответствует структурная схема при- веденная на (рис. 6.7).
110
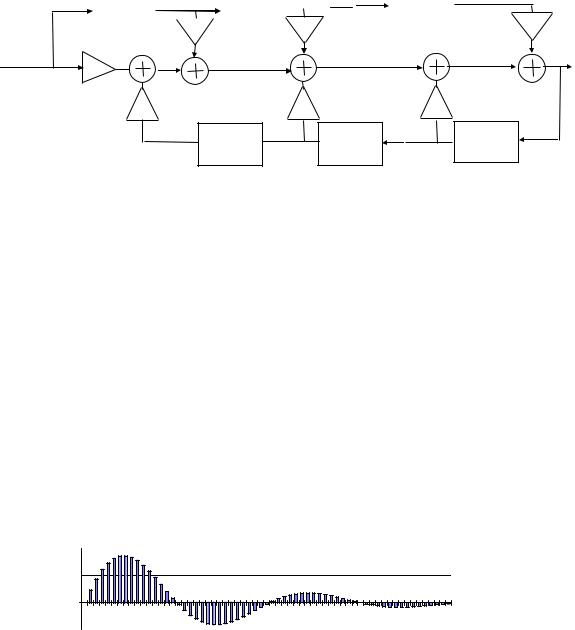
b0 |
b1 |
b2 |
|
bn |
|||||
|
z−1 |
|
|
|
z−1 |
|
|
z−1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Y[n]
X[n] |
|
-a2 |
-a1 |
-am-1 |
|||
-am |
−1 |
z−1 |
z−1 |
z |
|||
Рисунок 6.7 Схема решения разностного уравнения
6.4 Импульсные и частотные характеристики цифровой системы
Если на вход цифровой системы подать единичный цифровой им- пульс, то на выходе устойчивой системы будет наблюдаться переходной процесс, который называется импульсной характеристикой.
Линейная система с постоянными параметрами, импульсная харак- теристика которой является последовательностью конечной длины, назы- вается системой с конечной импульсной характеристикой. Пример им- пульсной характеристики { K[n] }, при n=1...64 конечной длины изображена на рис. 6.8.
K[n]
0.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.2 |
1 |
4 |
7 |
10 |
13 |
16 |
19 |
22 |
25 |
28 |
31 |
34 |
37 |
40 |
43 |
46 |
49 |
52 |
55 |
58 |
61 |
-0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.6.8 Импульсная характеристика конечной длины КИХ.
Системы с такой импульсной характеристикой всегда устойчивы, так как проверка на устойчивость сводится к суммированию конечного числа ограниченных слагаемых.
В отличие от определения, данного для КИХ систем, системой с бесконечной импульсной характеристикой (БИХ) называют системы, дли- ны импульсной характеристики которой не ограничиваются слева или справа.
111
