ЦСУ_Егоров

Импульсная характеристика системы (звена) используется для по- лучения отклика системы на произвольный входной сигнал.

Покажем теперь, что в линейной системе с постоянными парамет- рами входная и выходная последовательности связаны соотношением типа

и читается: "функция f1(t ) свёрнута с функцией f 2 (t)”.

Рассмотрим вычисление свёртки для дискретной последовательно- сти импульсов, определив связь между входной и выходной последова- тельностями.

Пусть на вход системы поступает последовательность

Пусть k[n]является откликом системы с постоянными параметрами на единичный импульс 10[n], а k[n − m] будет откликом системы на сме-

щенный импульс 10[n − m]. Из свойств линейности следует, что откликом на произвольный импульс x[m]10[n − m]должна быть последовательность x[m]k[n − m]. Поэтому откликом на произвольную решётчатую функцию

Выражение 6.41 имеет вид свёртки. Если сдвинуть начало отсчёта в точку m и учитывать только положительные значения этой переменной, что правомочно для реальных систем, то тогда уравнение свёртки будет представлено в следующем виде

Рассмотрим построение отклика системы на единичный ступенча- тый скачок 1[n], используя уравнение свёртки. Пусть система описывается разностным уравнением с постоянными параметрами

112

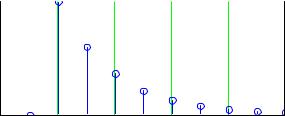
Подадим на вход системы единичный цифровой импульс и получим импульсную характеристику (рис. 6.9).

Затем подадим на вход системы три импульса, задержанных на 1, 2, 3 отсчёта и просуммируем отклики на эти импульсы (рис 6.10). При изме- нении задержки от 0 до ∞, получим отклик системы на единичный цифро- вой скачок.

Рассмотрим пример, выполненный в пакете Mathcad. Зададим чис- ловую последовательность x[n] состоящую из n=10 членов. Причем только x[2]=1, а остальные члены последовательности равны нулю.

Рисунок 6.9 Импульсная характеристика

Реакцию системы на единичный ступенчатый скачек можно рас- сматривать как сумму сдвинутых последовательно на один отсчет им- пульсных характеристик.

Создадим последовательность, где три члена последовательности будут равны единице x[2], x[3], x[4], а остальные – нулю.

Откликом входной последовательности будет сумма откликов на каждый входной импульс.

113

Рис. 6.10 Отклик системы на три единичных импульса

6.5. Автоматическое управление с использованием промышленных контроллеров

По принципу своего действия промышленный контроллер является устройством дискретного действия. Реализация программы обработки ин- формации осуществляется путем выполнения арифметических и некото- рых логических операций над кодами чисел: сложение, сравнение, пере- множение и т.д.

Для выполнения этих операций, а также операций кодирования и декодирования требуется время, поэтому ввод информации в промышлен- ный контроллер и вывод результатов решения производится в дискретные моменты времени.

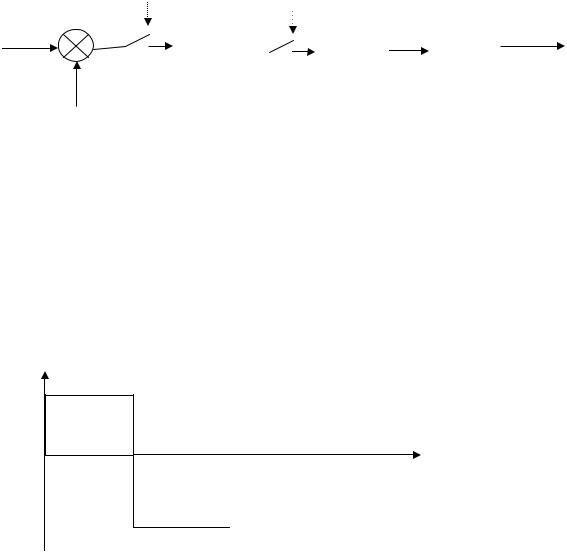
Операции кодирования и декодирования неизбежно связаны с кван- тованием сигнала по уровню. Однако при большом числе разрядов преоб- разователя непрерывного сигнала в код и кода в непрерывный сигнал квантованием по уровню можно пренебречь. В этом случае цифровая си- стема может исследоваться как обычная импульсная. Ее структурная схема может быть представлена как показано на рис. 6.11. На этой схеме переда- точная функция Д(z) отражает алгоритм обработки информации в цифро- вой вычислительной машине. Выходной сигнал промышленного контрол- лера может быть представлен импульсами прямоугольной формы с коэф- фициентом заполнения равным 1. Запоминание сигнала между импуль- сами моделируется звеном Wф(р) – фиксатором.[5]

114

В отличие от систем непрерывного действия динамические процес- сы в цифровых системах оказываются зависимыми от периода дискрети- зации Т.

Рассмотрим простейший разомкнутый контур (рис.6.13) с аналого- вым и цифровым регулятором, реализующим пропорциональный закон управления. Моделью объекта управления является апериодическое звено первого порядка.

Рассмотрим работу системы c аналоговым регулятором

и цыфровым регулятором:

Подадим на входы регуляторов гармонический входной сигнал:

X (t)

Генератор

Рисунок 6.13 Структурная схема системы с аналоговым и цифровым регуляторами

Промоделируем работу системы с цифровым регулятором. Период дискретизации Т1=0.05с, затем Т2=0.00005c. Для каждого из периодов дискретизации получены графики ошибки регулирования

σ(t) = y1 (t) − y 2 (t) (рис. 6.14-15).

116

Из графиков на рис. 6.14 рис. 6.15 видно, что для периода дискре- тизации значительно меньшего постоянной времени объекта управления цифровой регулятор с точки зрения математического описания может рас- сматриваться как непрерывный.

Рассмотрим замкнутые цифровые системы автоматического управ-

ления.

Наиболее часто замкнутые системы автоматического управления имеют параметрически-оптимизируемые регуляторы, реализующие П, ПИ или ПИД-регуляторы. Идеализированное уравнение ПИД регулятора име- ет вид:

где введены следующие обозначения К- коэффициент передачи,

Ти- постоянная времени интегрирования, Тд- постоянная времени дифференцирования,

σ (t) - рассогласование сигнала задания и обратной связи на входе регулятора.

y1(t)

1

t,c

Рисунок 6.14 Величина ошибки регулирования в цифровой системе при Т1=0,05 с равна σ max = 5%

117

y1(t)

1

t,c

σ (t)

3

t,c

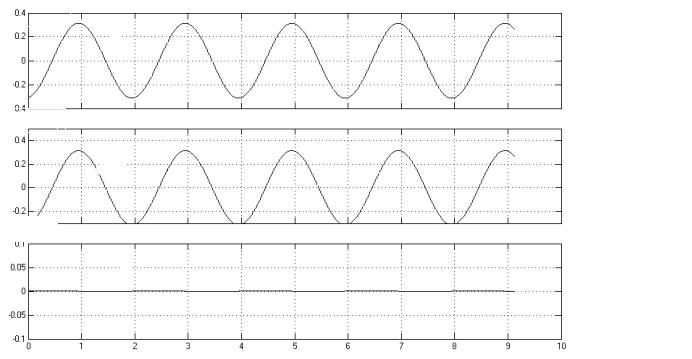
Рисунок 6.15 Величина ошибки регулирования в цифровой системе при Т1=0,00005 с равна σ max ≈ 0.

1.Выходной сигнал непрерывного контура.

2.Огибающая выходного сигнала цифрового контура.

3.Ошибка

Для малых тактов дискретизации, (Т<<То) когда время управляю- щего импульса значительно меньше постоянной времени непрерывной ча- сти системы, уравнение ПИД-регулятора можно преобразовать в разност- ное заменой производной разностью первого предела:

Непрерывное интегрирование может быть замечено интегрировани- ем по методу прямоугольников и трапеций. При использования метода прямоугольников получаем

В этом случае для формирования суммы необходимо помнить все преды- дущее значение сигнала σ [nT ]. Для программирования на ЦВМ долее

118

удобны рекуррентные алгоритмы. Эти алгоритмы отличаются тем, что для вычисления текущего значения управляющей переменной Uр[n] исполь- зуются ее предыдущие значения Up[n-1].

Для получения дискретного алгоритма достаточно из выражения (6.48) вычесть выражение для управляющего воздействия на предыдущем такте

Теперь к полученному ранее значению управляющей величины до- бавляется текущее приращение

Рассмотрим преобразование передаточных функций непрерывных звеньев в дискретные

Для этого представим выходной сигнал как уравнение свертки входного сигнала и импульсной характеристики

119

Последнее выражение (6.55) можно представить как изображение импульсной переходной характеристики и изображение входного сигнала.

Запишем дискретную передаточную функцию звена:

Переходя к переменной z = eTp , получим дискретную передаточ- ную функцию:

Используем выражение дискретной передаточной функции для преобразования передаточной функции непрерывного звена в дискретную.

Возьмем для примера апериодическое звено первого порядка с пе- редаточной функцией:

120

ного приведены на рис. 6.18.

Как видно из расчета параметров дискретной передаточной функ- ции и графиков, период дискретизации Т, соизмерим с постоянной време- ни. Существенно влияет на расхождения между кривой переходного про- цесса непрерывного звена и дискретного.

Графики переходных процессов апериодического звена (кривая 1) и дискретного (кривая 2) приведены на рис. 6.16.

y(t)

2

1

t

Рисунок 6.16. Графики переходных процессов апериодического звена первого порядка и дискретного

Если период дискретизации соизмерим с большой постоянной вре- мени объекта управления, то расчет цифрового регулятора представляет собой довольно сложную задачу. Однако современные промышленные контроллеры имеют довольно высокое быстродействие и целесообразно воспользоваться методами расчета аналоговых регуляторов [2]. В пакете Matlab программа Sisotool позволяет рассчитывать регуляторы методом амплитудно-частотных характеристик. В этом же пакете полученная пере- даточная функция регулятора непрерывного действия довольно просто преобразуется в дискретную.

121