
ЦСУ_Егоров
.pdf
х (t)
4 |
|
|
3 |
|
|
2 |
|
|
1 |
1 2 3 4 5 6 7 8 9 10 11 |
t |
|
|
Рисунок 3.1 Непрерывный сигнал
∙ Дискретный по времени непрерывный сигнал (рис. 3.2). Значе- ния сигнала определены только в определенный момент времени и нахо- дятся во всем непрерывно допустимом числовом диапазоне.
х [nT]
5
4
3
2
1 2 3 4 5 6 7 8 9 10 11 nT
Рисунок 3.2 Непрерывный сигнал дискретизированный по времени.
T - период отсчета сигнала (период дискретизации) n=0… ∞.
∙ Дискретный сигнал непрерывного времени (квантование по уровню) (рис. 3.3). Вся шкала возможных значений сигнала соответствует определенным уровням. Отсчеты сигнала производятся по времени непре- рывно.
х (t) |
1 |
2 |
|
|||||||
|
|
|
|
|
||||||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 3 4 5 6 7 8 9 10 11 12
Рисунок 3.3 Сигнал, квантованный по уровню. 1-исходный сигнал, 2-квантовый сигнал
∙Дискретный сигнал по уровню и по времени (рис. 3.4.)
Сигнал, который может принимать значения, в соответствии с определенными уровнями и отчеты производятся в дискретные моменты времени.
22
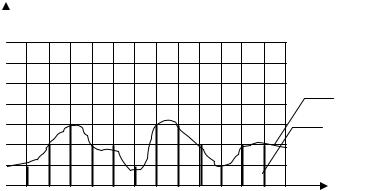
х[nT]
7 |
|
|
6 |
|
|
5 |
1 |
|
4 |
||
|
||
3 |
2 |
|
2 |
||
|
||
1 |
|
1 2 3 4 5 6 7 8 9 10 11 12 nT
Рисунок 3.4 Дискретный сигнал по уровню и по времени 1-исходный непрерывный сигнал, 2-дискретный сигнал по уровню и по времени
Современные системы автоматического управления выполняются на базе управляющих цифровых вычислительных машин. На вход цифро- вой системы могут подаваться непрерывные и дискретные сигналы. В слу- чае непрерывного сигнала он преобразуется аналого-цифровыми преобра- зователями в цифровой сигнал.
Цифровым называется дискретный сигнал, закодированный с по- мощью двоичной или двоично-десятичной системой.
Дискретные сигналы представляются числовыми последовательно- стями, у которых аргументом может быть номер значения отсчета этого сигнала.
Под дискретизацией сигнала по времени понимают преобразование модели сигнала функции непрерывного времени в функцию дискретного времени.
Под квантованием сигнала по уровню подразумевают преобразова- ние некоторой величины с непрерывной шкалой в величину, имеющую дискретную шкалу значений.
В цифровых системах каждое дискретное значение сигнала пред- ставляется последовательностью сигналов двух уровней. Наличие или от- сутствие импульса на определенном месте интерпретируется как 1 или 0 в соответствующем разряде двоичного числа.
Основным преимуществом передачи и обработки информации в цифровом коде является значительное снижение вероятности получения ошибочного результата по сравнению с передачей и обработкой информа- ции аналоговых сигналов. Это возможно по тому, что при использовании дискретных сигналов, во-первых, применимы такие методы кодирования, которые обеспечивают обнаружение и исправление ошибок, а во-вторых, можно избежать свойственного аналоговым сигналам эффекта накопления искажений в процессе их передачи и обработки. Представление информа-
23
ции в цифровой форме облегчает унификацию операции ее преобразования на всех этапах обращения.
На рисунке 3.5 показан пример преобразования непрерывного сиг- нала в цифровой код. Задано 8 уровней квантования в двоичной системе счисления с дискретностью отсчетов 1 с. Значения сигнала считываются с интервалом в 1 с. и полученным значениям присваивается двоичный код.
Рассмотрим более подробно операции дискретизации сигнала по времени и квантования. Для получения цифрового сигнала из непрерывно- го необходимо взять его отсчет в дискретные моменты времени t=nT, где t - текущее время, Т - интервалы между отсчетами, n - порядковый номер отсчета. Если полученный дискретный сигнал представить в функции дис- кретного времени, то полученная функция называется решетчатой (рис.3.6). В интервалах между отсчетами значение решетчатой функции равно нулю.
Дискреты могут определяться и для смещенных моментов времени, где смещение ∆Т может быть как положительным, так и отрицательным.
Решетчатая функция не обязательно должна формироваться из не- которой непрерывной функции. Любая числовая последовательность неко- торой величины, определенной в дискретные равноотстоящие моменты времени, может трактоваться как решетчатая функция.
X(t)
111
110
101
100
011
010
001
000
1 |
2 |
3 |
4 |
5 |
6 |
7 |
t |
X(t)
|
Цифровой код |
|
|
||||
Уровень “1” |
|
|
|
|
|
|
|
Уровень “0” |
2 |
3 |
4 |
5 |
6 |
7 |
t |
1 |
|||||||
Рисунок 3.5 Преобразование непрерывного сигнала в цифровой код
24

Рисунок 3.6 Решетчатая функция
Обратная задача - формирование непрерывной функции из решет- чатой не может быть решена однозначно. Функции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непре- рывных функций. Таким образом, основным моментом при проведении операции дискретизации является правильный выбор шага дискретизации, при котором возможно восстановить непрерывный сигнал с заданной по- грешностью.
Методы выбора дискретности зависят от модели представления сигналов. В реальных системах автоматического регулирования наиболь- шее распространение получила модель сигнала в виде случайного квази- стационарного процесса, каждая реализация которого представляет собой функцию с ограниченной спектральной плотностью сигнала. Величина шага дискретизации в этом случае ставится в зависимость от наивысшей частоты спектра рассматриваемого сигнала. Такой критерий выбора отсче- тов принято называть частотным.
Правило выбора предельного шага дискретизации с использовани- ем модели сигнала с ограниченным спектром в наиболее четкой форме сформулировано и доказано академиком В.А. Котельниковым в виде тео- ремы, получившей в отечественной литературе его имя. В зарубежной ли- тературе эту теорему называют теоремой Найквиста.
Теорема устанавливает принципиальную возможность полного вос- становления непрерывной функции с ограниченным спектром по ее отсче- там и указывает предельное значение интервала времени между отсчетами, при котором такое восстановление еще возможно. Формулируется она сле- дующим образом: Функция f(t), допускающая преобразование Фурье и имеющая непрерывный спектр, ограниченный полосой частот от f=0 до f= fmax где fmax=ωmax/2π - максимальная частотная составляющая спектра, пол- ностью определенная дискретным рядом своих мгновенных значений, вы- численных через интервал времени
T = |
1 |
. |
(3.1) |
|
2 f max
Физическая основа теоремы выявляется при рассмотрении связи между формой функции и шириной ее спектра. Только в случае, когда
25
спектр функции неограничен, ее значения в сколь угодно близкие моменты времени могут изменяться произвольно и скачкообразно. Сокращение вы- сокочастотной части спектра до граничной частоты ωmах равнозначно устранению из этой функции выбросов, которые могли быть сформирова- ны этими высокочастотными составляющими.
При меньших граничных значениях частоты ωmах частотного спек- тра непрерывная функция является более плавной и прослеживается связь между граничной частотой спектра ωmах и скоростью изменения функции во временной области.
Если воспользоваться теоремой В.А. Котельникова при выборе ша- га дискретизации, то вероятность случайного выброса функции на интер- вале времени Т является малой величиной.
Для определения граничной частоты fmах на практике иcпользуют два метода. Первый из них состоит в выборе настолько большой частоты fmах, чтобы составляющие с частотой выше fmах в сигнале были бы практи- чески невозможными и исходя из этого определенного значения выбрать частоту дискретизации в 2-4 раза больше.
Предположим, что для некоторого процесса возможное изменение сигнала в частотном спектре составит 0≤ f ≤1000 Гц. В соответствии с тео- ремой В.А.Котельникова интервал дискретизации следует взять ∆Т ≤ 0,5 мс.
При использовании второго метода выбора граничной частоты, сигнал предварительно фильтруется фильтром нижних частот. После фильтрации частотный спектр сигнала находится в пределах 0–f гр., где fгр– граничная частота пропускания фильтра.
Теперь если выбрать в fmax=fгр то в соответствии с теоремой Котель- никова частота дискретизации будет fд=2÷4 f гр.
Рассмотрим операцию квантования непрерывной функции по уров- ню. Поскольку числовое значение каждого отсчета должно быть выражено некоторым числом конечных цифр, то приближенно описать бесконечную последовательность возможных значений непрерывного процесса можно с помощью конечного числа уровней квантования. Как бы ни была точна шкала, необходимо сделать выбор между двумя соседними значениями. На рис.3.7 изображен процесс квантования непрерывного сигнала в соответ- ствии с разрешенными уровнями, происходящий в аналого-цифровом пре- образователе АЦП.
26

Рисунок 3.7 Квантование непрерывного сигнала:
а - непрерывный входной сигнал АЦП; б - выходной сигнал АЦП
Если отсчет сигнала меньше половины диапазона соседних уровней квантования, то ему присваивается значение нижнего уровня этого диапа- зона, если большее, то - верхнего уровня.
Таким образом, если квантование выполнено верно, то истинным значениям исходного непрерывного сигнала будут соответствовать наибо- лее близкие к ним уровни квантования. Точность приближения к непре- рывному процессу зависит от числа уровней квантования. В современных цифро-аналоговых преобразователях сигнал на выходе представляется в двоичном коде и имеет 1024 уровня квантования (десятиразрядное АЦП) и более. При идеальном преобразовании ошибка преобразования распре- делена равномерно с отклонением σх 0,29 х, где х шаг кантова- ния. В этом легко убедиться. Пусть р(х) - плотность вероятности ошибки равномерного квантования
|
1 |
|
− 0 ,5 x ≤ x ≤ 0 ,5 |
|
|
|
p(x) = |
|
при |
x |
, |
(3.2) |
|
|
||||||
|
x |
|
|
|
|
|
0 при других значениях х |
|
|
|
|||
где х текущее значение сигнала, соответствующее определенному уровню квантования (см. рис. 3.7). Очевидно, что среднее значение μх равно нулю, поскольку плотность р (х) симметрична относительно значения уровня. Тогда дисперсия ошибки
∞ |
x 2 p(x)dx = |
1 |
0 ,5 |
x |
|
0 ,25 |
x |
3 |
|
|||
σ x2 = ∫ |
∫ |
|
x 2dx = |
|
(3.3) |
|||||||
|
|
|
|
|
||||||||
−∞ |
|
|
|
x |
−0 ,5 |
x |
3 |
x |
|
|
||
и отклонение |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
(3.4) |
|
σ x = |
x |
2 |
≈ 0.29 x . |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
12 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
Это и есть среднеквадратичное значение ошибки квантования или шум квантования. При решении большинства прикладных задач, при
27
большом числе уровней квантования, погрешностью квантования по уров- ню непрерывного сигнала можно пренебречь. Если этого, по каким - то со- ображениям сделать не представляется возможным, то задача преобразо- вания непрерывного сигнала в дискретный должна рассматриваться как нелинейная, либо при квантовании по уровню нелинейность учитывается введением внешнего «шума».
Таким образом, если погрешность от квантования может быть до- вольно точно определена и учтена при обработке сигналов, то погреш- ность, связанную с дискретизацией, определить значительно сложнее. Не- правильный выбор шага дискретизации может полностью исказить вход- ной сигнал и привести к ошибкам при обработке информации.
Как было показано выше при цифровой обработке информации не- прерывный сигнал в АЦП, преобразуется в последовательность чисел, ко- торую можно рассматривать как решетчатую функцию, аргументом кото- рой является дискретное время [nT], где n = 0,1,2,3..., Т — период дискре- тизации.
Решетчатая функция может формироваться из непрерывной функ- ции либо из любой числовой последовательности некоторой величины, определенной в равноотстоящие моменты времени.
3.2. Частотная форма представления детерминированных сигналов
При анализе работы систем автоматического управления сложный сигнал f(x) можно представить в виде взвешенной суммы базисных функ-
ций ψk (t) [1]
f ( x ) = ∑Ckψ k (t ), |
(3.5) |
k
где Сk- базисные коэффициенты; [t1,t2]-интервал существования сигнала.
Совокупность базисных коэффициентов Сk называется дискретным спектром сигнала. Вычисление спектральных составляющих сигнала су- щественно облегчается при выборе в качестве базиса системы ортогональ- ных функций. Систему функций ψk, ψm называют ортогональной на отрез- ке [t1, t2], если для всех k=0…n, m=0…n за исключением k=m удовлетворя- ется условие:
t2 |
|
∫ψ k ( t )ψ m ( t ) = 0 . |
(3.6) |
t1 |
|
Эта система функций будет ортонормированной, если для всех k=m справедливо соотношение:
28

t2 |
|
∫ψ m2 ( t )dt = 1 . |
(3.7) |
t1
При анализе систем автоматического управления широко использу- ется представление детерминированных сигналов с применением базисных функций ept. При p=±jω-преобразование Фурье, а при p=s±jω- преобразование Лапласа.
Использование экспоненциальных базисных функций в преобразо- вании Фурье комплексно сопряженными парами (с положительным и от- рицательным параметром ω) позволяет в соответствии со следствием фор- мулы Эйлера:
e jω + e |
− jω |
|
eiω − e |
−iω |
||
|
|
= cosωt; |
− j |
|
|
= sin ωt (3.8) |
2 |
|
2 |
|
|||
|
|
|
|
|
||
представить сложный детерминированный сигнал в виде суммы гармони- ческих составляющих. Поскольку параметр ω в этом случае имеет смысл круговой частоты, результат такого преобразования называют частотной формой представления сигнала.
Рассмотрим разложение в ряд Фурье периодических функций. Пусть функция х(t) , заданная на интервале времени t1≤ t ≤ t2 и удо-
влетворяющая условиям Дирихле повторяется с периодом T = 2π = t2-t1,
ω
на протяжении времени от − ∞ до +∞, где ω - угловая частота изменения этого сигнала. Эта функция может быть представлена в виде ряда
∞ |
|
x(t) = ∑Ck e jkωt . |
(3.9) |
k =−∞
Запишем ряд Фурье в форме вещественной функции и перейдем от двухстороннего представления ряда, содержащего отрицательные частоты к одностороннему.
Обозначим
Ck |
= |
ak + jbk |
;C−k |
= |
ak − jbk |
, |
|
|
|
(3.10) |
|||
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||
тогда |
2 |
|
|
2 |
|
|
|
|
|
|
|||
∞ |
|
|
|
∞ |
e jkωt + e− jkωt |
|
e jkωt − e− jkωt |
|
|||||
|
|
|
|
|
|
||||||||
x( t ) = C0 + |
∑Cke jkωt |
+ C−ke− jkωt |
= C0 + ∑ak |
|
|
+ bk j |
|
. |
(3.11) |
||||
2 |
2 |
||||||||||||
|
k=1 |
|
|
|
k=1 |
|
|
|
|||||
В соответствии с формулой Эйлера получим окончательное выра- жение для ряда Фурье в тригонометрическом виде:
29

∞ |
|
x(t) = a0 + ∑ak cos(kωt) + bk sin (kωt) |
(3.12) |
k=1
Вразложении периодического сигнала в ряд участвуют гармоники с начальной частотой ω, дискретно изменяющейся при изменении k от 0 до ∞.
Определим значения коэффициентов ak, bk, используя для этого ор- тонормированную систему функций. В качестве второй базисной функции
выберем ψ m (t ).
ψ m |
(t ) = e |
− jm ω t |
. |
(3.13) |
|
|
|
Действительно, при k ≠ m интеграл произведения базисных функ-
ций
t2
∫e jkωt e − jmωt dt = 0 .
t1
А при значениях k=m под интегральная функция равна 1. Опреде- ленный интеграл на интервале интегрирования, равным периоду функции равен T.
Умножим правую и левую части ряда на вторую базисную функ- цию е− jkωt и осуществим интегрирование на интервале t1, t2
t2 |
|
∞ |
|
|
∫ x(t )e |
− jmωt dt = |
∑ ∫ C k e jkωt e |
− jmωt dt , |
(3.14) |
t1 |
|
k =−∞ |
|
|
при m=k получим:
t
∫2 x (t )e − jk ωt dt = TC k ,
t1
C k |
= |
1 |
|
t 2 |
x (t )e − jk ω t dt . |
|
|
|
|
||||
T |
∫ |
|
|
|
|
||||||||
|
|
|
|
|
|
t |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запишем выражение (3.16) в виде: |
|
|
|||||||||||
|
|
1 t2 |
|
|
e jkωt + e − jkωt |
|
e jkωt − e |
− jkωt |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C k |
= |
|
|
∫ x(t ) |
2 |
− j |
|
dt = |
|||||
|
T |
t1 |
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
= 1 t∫2 [x(t )cos(kωt )dt − jx(t )sin(kωt )]dt .
T t1
В соответствии с обозначением
C k = α k + jbk ,
2
определим aк, bк:
(3.15)
(3.16)
(3.17)
(3.18)
30

t2
αk = T2 ∫ x(t )cos(kωt )dt , (3.19)
t1
t2
bk = T2 ∫ x(t )sin(kωt )dt . (3.20)
t1
При k=0 получим, в соответствии с (3.16), составляющую
t2
C0 = 1 ∫x(t )dt (3.21)
Т t1
и через принятое обозначение:
α = |
2 |
|
t2 |
x(t )dt , |
a = 2C . |
|
|||
|
∫ |
(3.22) |
|||||||
|
|||||||||
0 |
T |
|
0 |
0 |
|||||
|
|
|
|
|
|||||
|
|
|
|
t1 |
|
|
|
|
|
Окончательно в тригонометрическом виде ряд периодической |
|||||||||
функции запишется так: |
|
|
|
||||||
|
|
|
|
|
∞ |
|
|
|
|
x(t ) = α 0 + ∑[α k cos(kωt )+ bk sin(kωt )]. |
(3.23) |
||||||||
|
2 |
|
k =1 |
|
|
|
|||
Таким образом, любой сложный детерминированный периодиче- ский сигнал можно представить в виде суммы ряда гармонических состав- ляющих .
При записи ряда Фурье в комплексной форме функцию
C k |
= |
1 |
t 2 |
x (t )e − jk ω t dt |
(3.24) |
|
T |
∫ |
|||||
|
|
|
t |
1 |
|
|
|
|
|
|
|
|
|
принято называть комплексным спектром периодического сигнала этот спектр дискретный т.к. значения Сk определены на числовой оси толь- ко для целых значений k.
Обозначим в выражении (3.17)
|
1 |
t2 |
|
|
|
|
|
|
1 |
t2 |
|
|
|
× ∫ x(t) × cos(kωt)dt |
через Аk(kω) , а |
j × |
× ∫ x(t) ×sin(kωt)dt |
че- |
|||||||
|
|
T |
T |
|||||||||
|
|
t |
|
|
|
|
|
|
t |
|
||
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
рез |
Вk(kω), |
тогда коэффициент Сk |
в |
комплексном виде |
равен, |
|||||||
Ck |
= Ak (kω) + jBk (kω) |
и модуль |
этой |
комплексной функции |
||||||||
A(kω ) определяет значение частотного спектра |
|
|
||||||||||
|
|
A(kω) = |
|
|
. |
|
|
|
|
(3.25) |
||
|
|
|
Ak2 (kω) + Bk2 (kω) |
|
|
|
|
|||||
Частотный спектр удобно представить спектральными диаграмма- ми. На диаграмме спектра каждой гармонике в соответствии ставится вер- тикальный отрезок, длина которого пропорциональна значению модуля коэффициента Сk. На оси абсцисс откладываются частоты, кратные основ- ной частоте. Причем каждому значению модулю коэффициента Сk соот- ветствует определенная частота.
31
