
ТФКП-15.03.14
.pdf
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ОДЕСЬКА НАЦІОНАЛЬНА АКАДЕМІЯ ХАРЧОВИХ ТЕХНОЛОГІЙ
Вашпанова Р.В.,Угольніков О.П.
ВИЩА МАТЕМАТИКА
ТЕОРІЯ ФУНКЦІЙ КОМПЛЕКСНОЇ ЗМІННОЇ
Навчальний посібник
Одеса - 2014
Вашпанова Н.В., Угольніков О.П. Вища математика. Теорія функцій комплексної змінної: навчальний посібник. Одеська державна академія холоду, 2012. – 88 с.
У посібнику висвітлюється один із важливих розділів курсу вищої математики: теорія функцій комплексної змінної. У логічній послідовності викладаються основні поняття розділу, починаючи з арифметики комплексних чисел і закінчуючи застосуванням теорії до обчислення деяких визначених та невласних інтегралів від функцій дійсної змінної методом лишків.
Навчальний посібник призначено для студентів, що навчаються за напрямами підготовки 050101 – «Комп’ютерні науки», 050102 – «Комп’ютерна інженерія», 050304 – «Нафтогазова справа», 050601 – «Теплоенергетика», 050604 – «Енергомашинобудування», 050701 – «Електротехніка та електротехнології».
Рецензент: Швець В.Т., д. ф.-м. н., професор Одеської національної академії харчових технологій.
Розглянуто та рекомендовано до видання на засіданні кафедри прикладної математики.
Протокол № __ від “___” ___________ 2014 р.
Розглянуто та рекомендовано до видання на засіданні науково-методичної Ради з напрямів підготовки 6.050101 «Комп’ютерні науки» та 6.050102 «Комп’ютерна інженерія».
Протокол № __ від “___” ___________ 2014 р.
ОНАХТ, 2014
2
Зміст |
|
1. Комплексні числа ............................................................................................ |
5 |
1.1. Основні поняття ........................................................................................ |
5 |
1.2. Геометрична інтерпретація комплексних чисел.................................... |
7 |
1.3. Форми запису комплексних чисел .......................................................... |
8 |
1.3.1. Алгебраїчна форма запису комплексного числа............................. |
8 |
1.3.2. Тригонометрична форма запису комплексного числа ................... |
9 |
1.3.3. Показникова форма запису комплексного числа.......................... |
10 |
1.3.4. Піднесення до степеня комплексного числа ................................. |
11 |
1.3.5. Добування кореня з комплексного числа ...................................... |
12 |
2. Диференціальне числення функцій комплексної змінної......................... |
14 |
2.1. Області на комплексній площині .......................................................... |
14 |
2.2. Стереографічна проекція комплексної площини на сферу ................ |
15 |
2.3. Функції комплексної змінної................................................................. |
16 |
2.3.1. Алгебраїчні функції ......................................................................... |
17 |
2.3.2. Показникова функція ....................................................................... |
18 |
2.3.3. Логарифмічна функція..................................................................... |
18 |
2.3.4. Тригонометричні функції ................................................................ |
19 |
2.3.5. Обернені тригонометричні функції................................................ |
21 |
2.3.6. Гіперболічні функції ........................................................................ |
21 |
2.3.7. Обернені гіперболічні функції ........................................................ |
23 |
2.4. Границя та неперервність функції комплексної змінної .................... |
23 |
2.5. Диференціювання функції комплексної змінної ................................. |
24 |
2.6. Інтеграл від функції комплексній змінній ........................................... |
26 |
2.6.1. Лінії на комплексній площині......................................................... |
26 |
2.6.2. Означення та властивості інтеграла ............................................... |
27 |
2.6.3. Інтегрування аналітичних функцій ................................................ |
29 |
2.6.4. Інтегральна формула Коші .............................................................. |
33 |
2.6.5. Визначення аналітичної функції за її дійсною частиною ............ |
35 |
3. Ряди аналітичних функцій і ізольовані особливі точки ............................ |
37 |
3.1. Числові та степеневі ряди ...................................................................... |
37 |
3.2. Ряди Тейлора та Маклорена .................................................................. |
38 |
3.3. Ряд Лорана ............................................................................................... |
40 |
3.4. Деякі прийоми розкладу функцій в ряд Лорана .................................. |
44 |
3.5. Нулі та ізольовані особливі точки аналітичної функції ..................... |
45 |
3.5.1. Нулі аналітичної функції ................................................................. |
45 |
3.5.2. Ряд Лорана функції f (z) в околі її скінченної ізольованої |
|
особливої точки z0 ..................................................................................... |
46 |
3.5.3. Ряд Лорана функції
f (z)
в околі її нескінченно віддаленої
ізольованої особливої точки z ............................................................ |
48 |
3.6. Ізольовані особливі точки деяких елементарних функцій ................. |
49 |
4. Лишки функції та їх застосування............................................................... |
51 |
4.1. Лишок функції у скінченній ізольованій особливій точці ................. |
51 |
4.2. Лишок функції у нескінченно віддаленій особливій точці ................ |
54 |
3
4.3. Основна теорема про лишки.................................................................. |
|
|
|
|
55 |
|||||||
4.4. Обчислення деяких інтегралів за допомогою лишків......................... |
57 |
|||||||||||
4.4.1. Інтеграли |
|
2 |
|
|
|
|
|
|
( R |
– раціональна функція) |
58 |
|
I |
|
R(cos , |
sin ) d |
|||||||||
|
|
|
|
|
|
|||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.4.2. Інтеграли вигляду |
I |
|
R(x) d x |
( R |
– раціональна функція) |
59 |
||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.4.3. Інтеграли вигляду I |
|
e |
iax |
f (x)dx |
. Лема Жордана |
60 |
||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Приклади розв’язання завдань |
|
|
|
|
|
|
63 |
|||||
6. Завдання для самостійного розв ......................................................’язання |
|
|
72 |
|||||||||
7. Бібліографічний список ................................................................................ |
|
|
|
|
|
|
|
|
85 |
|||
8. Предметний покажчик |
.................................................................................. |
|
|
|
|
|
|
|
|
86 |
||
4
1. Комплексні числа
1.1. Основні поняття
Два дійсних числа
x
та
y
будемо називати впорядкованою парою, як-
що заданий порядок запису цих чисел: на першому
гому – |
y . Упорядковану пару дійсних чисел |
x |
та |
|
|
|
місці число |
x |
, на дру- |
|
|
|
|
|
y |
будемо записувати у |
||
вигляді |
(x, y) . |
Комплексним числом z називається впорядкована пара дійсних чисел
z (x, y) , перше з яких x називається дійсною частиною, а друге |
y |
– уяв- |
ною частиною цього комплексного числа. Вони відповідно позначаються:
x Re z , y Im z .
Зокрема, при y 0 комплексне число z (x, 0) x є дійсним числом. Це позволяє включити множину дійсних чисел у множину комплексних чисел. При x 0 комплексне число z (0, y) називається чисто уявним.
Два комплексних числа
z |
(x |
, y ) |
1 |
1 |
1 |
та
z |
2 |
(x |
, y |
2 |
) |
|
2 |
|
|
називаються рівними,
якщо вони мають рівні дійсні та уявні частини, тобто:
z |
z |
|
|
x |
x |
, |
||
|
|
1 |
2 |
|
|
|||
|
|
|
|
|
|
|||
1 |
|
2 |
|
y |
y |
|
, |
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
2 |
|
||
або
Re z |
Re z |
, |
||
|
1 |
2 |
|
|
Im z |
Im z |
. |
||
|
||||
1 |
2 |
|
||
Комплексне число |
z (x, y) |
дорівнює нулю, якщо |
x 0, y 0 . |
Комплексне число z (x, y) називається комплексно спряженим до числа z (x, y) , якщо воно відрізняється тільки знаком уявної частини.
Дамо означення операцій додавання та множення комплексних чисел. Оскільки дійсні числа є частиною множини комплексних чисел, ці означення повинні бути такими, щоб для комплексних чисел виконувалися ві-
домі правила дій над дійсними числами. |
|
|
Сумою двох |
комплексних чисел z1 (x1, y1 ) і |
z2 (x2 , y2 ) називається |
комплексне число |
z вигляду |
|
|
|
z z1 z2 (x1 x2 , y1 y2 ) . |
|
Добутком двох комплексних чисел z1 (x1, y1 ) і |
z2 (x2 , y2 |
||
комплексне число |
z |
вигляду |
|
z z1 z2 (x1x2 y1 y2 , x1 y2 x2 y1) .
Легко перевірити, що сума та добуток комплексних чисел самі властивості, що й сума та добуток дійсних чисел:
1. z1 z2 z2 z1 (переставна властивість суми);
2. (z1 z2 ) z3 z1 (z2 z3 ) (сполучна властивість суми);
|
(1.1) |
) |
називається |
(1.2)
мають такі ж
3.z (0, 0) z (особлива роль числа (0, 0) );
4. |
Для |
кожного |
числа z (x, y) існує протилежне йому число |
|
|
z ( x, y) таке, що z z (0, 0) ; |
|||
5. |
z1 z2 |
z2 z1 (переставна властивість добутку); |
||
6. |
(z1 z2 ) z3 |
z1 (z2 |
z3 ) (сполучна властивість добутку); |
|
7. |
z (1, 0) z |
(особлива роль числа (1, 0) ); |
||
5
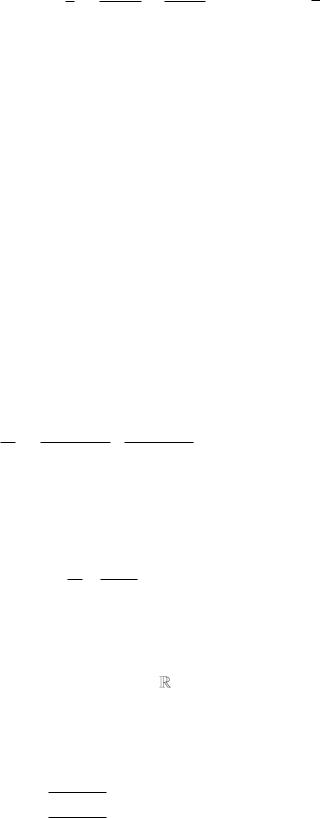
8. |
Для будь-якого комплексного числа z (x, y) , |
|
відмінного |
|||||||||
|
існує обернене йому число |
1 |
|
|
|
x |
2 , |
|
y |
|
|
таке, що z |
|
|
|
2 |
y |
2 |
y |
2 |
|
||||
|
|
z |
|
x |
|
x |
|
|
|
|
||
9. |
(z1 z2 ) z3 z1 z3 z2 z3 (розподільна |
властивість добутку |
||||||||||
від нуля,
|
1 |
(1, 0) |
; |
|
z |
||||
|
|
|
відносно
суми).
Скориставшись цими властивостями, можна дати означення операцій віднімання та ділення комплексних чисел як операцій, обернених до опе-
рацій додавання та множення, відповідно. |
|
|
|
||
Різницею комплексних чисел |
z1 (x1 |
, y1 ) |
і |
z2 (x2 , y2 ) |
називається ком- |
плексне число z , яке у сумі з числом z2 |
дає z1 . Очевидно, що число z має |
||||
вигляд |
|
|
|
|
|
z z1 z2 |
(x1 x2 , y1 |
y2 ) . |
(1.3) |
||
Часткою комплексних чисел |
z1 (x1, y1 ) |
і z2 (x2 , |
y2 ) 0 називається |
||
комплексне число |
z , яке при множенні на число |
z2 |
дає z1 . Дійсна |
x |
та уяв- |
||||
|
|
|
|
|
|
|
|
|
|
на y частини частки |
z |
знаходяться як розв’язок лінійної системи алгебраї- |
|||||||
чних рівнянь |
|
|
|
|
|
|
|
|
|
|
|
|
x x y |
2 |
y x |
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
з визначником маємо
y |
x x |
y y |
2 |
2 |
1 |
x2 |
y2 |
, відмінним від нуля. Розв’язавши цю систему, отри- |
||||||||||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
z |
x x |
|
y y |
|
, |
x y |
x y |
|
|
(1.4) |
|||||||
|
|
|
1 |
|
1 |
2 |
1 |
2 |
2 |
|
1 |
1 |
2 |
. |
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
z |
|
|
|
x |
2 |
y |
2 |
|
|
x |
2 |
y |
2 |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|||||||
З практичної точки зору ділення комплексних чисел виконується ін-
акше: щоб знайти частку комплексних чисел z1 (x1, y1) і |
z2 (x2 , y2 ) , ділене |
||||||||||||||
та дільник необхідно помножити на число |
z2 |
, комплексно спряжене до ді- |
|||||||||||||
льника: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
z |
|
z |
z |
|
|
. |
|
(1.4') |
|||
|
|
|
|
1 |
|
1 |
|
2 |
|
||||||
|
|
|
|
z |
2 |
|
z |
2 |
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Приклади. Виконати дії: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) |
3 (x, y) (3, 0) (x, y) (3x 0, 3y 0) (3x, 3y) . |
|
|
||||||||||||
Взагалі, очевидно, при будь-якому дійсному має місце рівність |
|||||||||||||||
|
|
|
(x, y) ( x, y), |
|
; |
|
|||||||||
2) |
(0, 1) |
2 |
(0, 1) (0, 1) ( 1, 0) 1 |
|
|
(0, 1) |
2 |
|
1. |
|
|||||
|
|
|
|
|
|||||||||||
Комплексне число (0,1) i називається уявною одиницею. Згідно з означенням добутку комплексних чисел квадрат уявної одиниці дорівнює мінус одиниці:
 i2 1
i2 1  .
.
Чисто уявне комплексне число (0, y) можна розглядати як добуток уявної одиниці (0,1) i та дійсного числа (y, 0) .
6
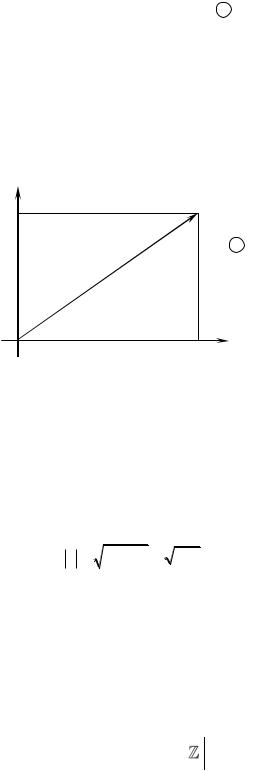
1.2. Геометрична інтерпретація комплексних чисел
При вивченні властивостей комплексних чисел дуже зручною є їх геометрична інтерпретація. Оскільки комплексне число задається парою дій-
сних чисел, то комплексне число |
z (x, y) |
можна зобразити точкою коорди- |
|
|
натної площини з координатами (x, y) . Числу z 0 ставиться у відповідність початок координат даної площини. Таку площину ми далі будемо називати
комплексною площиною і позначати символом |
z |
, вісь абсцис – дійсною |
віссю, ось ординат – уявною віссю. При цьому встановлюється взаємно однозначна відповідність між множиною всіх комплексних чисел та множиною точок комплексної площини, а також між множиною всіх комплекс-
них чисел |
z (x, y) |
та множиною радіус-векторів точок з координатами |
|
|
|
|
|
(x, y) |
. При такому способі зображення додавання та віднімання комплекс- |
||
|
|
|
|
них чисел зводиться до додавання та віднімання відповідних векторів.
y
φ
O
r
x
z
z
y
x
Мал. 1.
Якщо крім декартової |
ввести полярну систему координат так, щоб по- |
люс знаходився у початку |
O декартової системи, а полярна вісь була на- |
прямлена вздовж додатного напряму осі абсцис, то полярними координа- |
|
тами точки |
z |
будуть z z(r, ) , де |
r |
– відстань від точки до початку коор- |
динат. Довжина r радіус-вектора точки, що відповідає комплексному числу z , називається модулем комплексного числа і дорівнює
r z |
x |
2 |
y |
2 |
|
z z . |
|
|
|||||
Кут між радіус-вектором r точки z |
|
та додатним напрямом дійсної вісі |
||||
називається аргументом комплексного числа z . Цей кут вважається додатним, якщо він відраховується проти ходу годинникової стрілки і визначається не однозначно, а з точністю до адитивного доданку, кратного до 2 .
У зв’язку з цим розрізняють повне значення аргументу |
Arg z |
та його головне |
|||
|
|
|
|
|
|
значення arg z . Тоді, очевидно, |
|
|
|
|
|
|
|
|
|
|
|
|
Arg z 2k |
k . |
|
|
|
|
|
|
|
|
|
7

Областю визначення |
arg z може бути довільний проміжок довжиною |
2 . |
|
Надалі ми будемо вважати, що |
( , ] . Головне значення аргументу |
||
комплексного числа |
z (x, y) визначається співвідношеннями |
|
|
|
|
y |
|
|
ІІ |
І |
|
=arctg |
y |
|
|
x |
|||
|
|
||
|
|
O |
=arctg xy
ІІІ
=arctg |
y |
|
x |
||
|
||
x |
|
=arctg xy
ІV
Якщо точка, що зображує відповідне комплексне число, лежить на одній з осей координат, то значення аргументу є очевидним і не вимагає окремого обчислення. Зокрема для комплексного числа z 0 модуль дорівнює нулю, а аргумент не визначений.
Два відмінних від нуля комплексних числа рівні тоді і тільки тоді, коли їх модулі і головні значення аргументів рівні, а аргументи рівні або відрізняються на доданок, кратний до 2 :
z |
z |
|
|
r |
r |
, |
|
|
|
|
1 |
2 |
|
|
|||
|
|
|
|
|
|
|
||
1 |
|
2 |
|
|
|
, |
||
|
|
|
|
|
1 |
|
2 |
|
або
z |
|
z |
2 |
, |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Arg z |
|
2k . |
||
Arg z |
2 |
||||||
|
|
1 |
|
|
|
|
|
Комплексно спряжені числа мають рівні модулі, а головні значення аргументів відрізняються знаком:
z z , arg z arg z |
(arg z ) |
|
|||||
|
|
|
|
|
|
. |
|
Модуль різниці двох комплексних чисел |
z1 |
та |
z2 має геометричне |
||||
значення відстані між відповідними точками на комплексній площині: |
|||||||
z1 z2 (x2 x1) |
2 |
( y2 y1) |
2 |
. |
|
||
|
|
|
|||||
Відмітимо, крім того, очевидні нерівності |
z x, |
z y . |
|
||||
1.3. Форми запису комплексних чисел
Існують три форми запису комплексних чисел: алгебраїчна, тригоно-
метрична і показникова.
1.3.1. Алгебраїчна форма запису комплексного числа
Розглянемо комплексне число z (x, y) . Його можна записати у такому вигляді:
(x, y) (x, 0) (0, y) (x, 0) (0, 1) ( y , 0) (x, 0) i ( y , 0) x i y.
Таким чином, ми отримали алгебраїчну форму запису комплексного числа:
z x i y |
(1.5) |
|
|
Алгебраїчна форма запису дозволяє виконувати арифметичні дії з комплексними числами як з многочленами з використанням правил алгебри:
8

z |
|
z |
2 |
(x |
i y ) (x |
i y |
) (x |
x |
) i ( y |
y |
|
), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
|
|
|
1 |
|
|
1 |
2 |
|
|
2 |
|
|
|
1 |
|
|
2 |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z |
|
z |
2 |
(x |
i y ) (x |
i y |
) (x |
x |
) i ( y |
y |
2 |
), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
|
|
|
1 |
|
|
1 |
2 |
|
|
2 |
|
|
|
1 |
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
z |
|
z |
|
(x i y ) (x i y |
) x x |
i x y |
|
i x y |
i |
2 |
y y |
|
(x x |
|
|
y y |
) |
||||||||||||||||||||||||||
|
2 |
2 |
|
2 |
2 |
||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
1 |
|
1 |
|
2 |
|
2 |
|
|
1 |
2 |
|
|
|
1 |
|
2 |
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
2 |
|
|
|
||||||
z |
|
x |
i y |
|
|
(x |
i y ) (x |
|
i y |
) |
|
(x x y y |
) i (x y |
x y |
) |
|
x x |
|
|||||||||||||||||||||||||
|
1 |
|
1 |
1 |
1 |
|
1 |
|
|
2 |
|
|
2 |
|
|
|
1 |
2 |
1 |
2 |
|
|
|
|
|
|
2 |
1 |
1 |
|
2 |
|
|
1 |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
z |
|
|
|
x |
i y |
|
|
(x |
i y |
) (x |
i y |
) |
|
|
|
|
|
|
x |
2 |
y |
2 |
|
|
|
|
|
|
|
|
|
x |
2 |
||||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
2 |
|
|
2 |
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||
|
|
|
Приклад. Для комплексних чисел |
|
z1 |
2 i |
та |
|
z2 |
1 2i |
|
||||||||||||||||||||||||||||||||
ницю, добуток та частку |
z1 |
/ z2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Розв’язання. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
i (x y |
2 |
x y ), |
|
|
|
|
|||||
1 |
2 |
1 |
|
|
|
|
|
|
|||
y y |
|
i |
x y |
x y |
|
. |
|||||
1 |
|
2 |
2 |
|
1 |
1 |
2 |
||||
|
|
|
|
||||||||
y |
2 |
|
|
|
x |
2 |
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
2 |
|
2 |
|
|
|
знайти суму, різ-
|
|
z |
|
z |
2 |
(2 i) (1 2i) (2 1) (1 2)i 3 i; |
|
|
|
||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
z |
|
z |
2 |
(2 i) (1 2i) (2 1) (1 2)i 1 3i; |
|
|
|||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
z |
|
z |
|
(2 i) (1 2i) 2 i 4i 2i |
2 |
4 3i; |
|
|
|
|
|
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
z |
|
|
2 i |
|
(2 i) (1 2i) |
|
2 i |
4i 2i |
2 |
|
5i |
|
|
||||||||||||||
|
|
|
|
|
|
|
i. |
|
|||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
1 2i |
|
(1 |
2i) (1 2i) |
1 |
4i |
2 |
|
|
|
|
5 |
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.3.2. Тригонометрична форма запису комплексного числа |
|
||||||||||||||||||||||||||||
Декартові координати |
(x, y) |
точки z |
зв’язані з її полярними координа- |
||||||||||||||||||||||||||
тами |
(r, ) |
відомими з геометрії співвідношеннями (див. мал.1): |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x r cos , |
y r sin |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Підставивши ці співвідношення в (1.5), одержимо: |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
z x i y r cos i r sin r(cos isin ) |
. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже, ми отримали тригонометричну форму запису комплексного числа: |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z r(cos isin ) |
|
|
|
|
|
|
|
|
|
(1.6) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Тригонометрична форма запису є дуже зручною для виконання опе- |
|||||||||||||||||||||||||||||
рацій множення і ділення комплексних чисел. Нехай |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
z1 |
r1(cos 1 isin 1), |
z2 r2 (cos 2 |
i sin 2 ) , |
|
|||||||||||||||||||||
тоді за правилом множення комплексних чисел матимемо: |
|
||||||||||||||||||||||||||||
|
|
z r(cos i sin ) z |
z |
2 |
r (cos i sin ) r (cos |
2 |
i sin |
) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
1 |
|
|
1 |
|
|
|
2 |
|
|
|
|
2 |
|
||
r1 r2 (cos 1 cos 2 sin 1 sin 2 ) i(sin 1 cos 2 cos 2 sin 1)
r1 r2 cos( 1 2 ) i sin( 1 2 ) .
Остаточно
1 |
z |
2 |
1 2 |
|
|
1 |
2 |
1 |
2 |
|
, |
(1.7) |
z |
|
r r |
|
|
cos( |
|
) i sin( |
|
) |
|
|
тобто при множенні двох комплексних чисел їх модулі перемножуються, а аргументи додаються.
Аналогічно, при діленні числа z1 на число z2 0 маємо:
z |
z1 |
|
r1 |
cos( |
|
|
) i sin( |
|
|
) , |
(1.8) |
|
|
2 |
2 |
||||||||
|
z2 |
|
r2 |
1 |
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
тобто при діленні комплексних чисел їх модулі діляться, а аргументи віднімаються.
Приклад. Записати у тригонометричній формі наступні комплексні числа, взявши головне значення аргументу:
1) z 1; |
2) z 2; |
3) z i; |
4) z 3i; |
5) z 1 i. |
Розв’язання.
9

1)
2)
3)
4)
|
|
|
|
|
2 |
|
2 |
|
|
. Оскільки комплексному числу відповідає |
||||||||||||||||||||
z 1, r |
|
z 1 |
0 |
|
1 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
точка, що лежить на дійсній додатній півосі, то |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
arg z arctg0 0 |
. |
|
|
|
|
|
|
|
|
|||||||||||||
Отже, |
z |
1 (cos0 isin 0) |
– тригонометрична форма. |
|
|
|
|
|||||||||||||||||||||||
В даному випадку r |
z |
|
( 2) |
2 |
0 |
2 |
2 . Оскільки комплексному числу |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
відповідає точка, що лежить на дійсній від’ємній півосі, то |
, а |
|||||||||||||||||||||||||||||
комплексне число в тригонометричній формі виглядає так: |
|
|
||||||||||||||||||||||||||||
r z |
|
|
|
1 1 |
|
|
|
z 2 (cos isin ) . |
|
|
|
|
|
|
|
|
|
|
||||||||||||
0 |
|
|
. Оскільки комплексному числу відповідає точка, |
|
||||||||||||||||||||||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
що належить уявній додатній півосі, то |
arg z |
|
. Тому число |
z |
||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в тригонометричній формі матиме вигляд |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
z cos |
|
i sin |
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
r z |
0 |
|
( 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
2 |
3 . Оскільки комплексному числу відповідає точ- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ка, що належить уявній від’ємній півосі, то |
arg z |
|
, а число |
|||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z в тригонометричній формі є |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
z 3 cos |
2 |
i sin |
|
2 |
. |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5) Знайдемо модуль комплексного числа: r  1 i
1 i

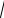 12 12
12 12 
 2 . Оскільки точка, що відповідає даному числу, належить першому коор-
2 . Оскільки точка, що відповідає даному числу, належить першому коор-
динатному куту, то arctg1 |
|
. Тоді тригонометрична форма є |
|||||
4 |
|||||||
|
|
|
|
|
|
||
z |
|
|
|
i sin |
|
|
|
|
|||||||
2 cos |
|
|
. |
||||
|
|
|
4 |
|
4 |
|
|
1.3.3. Показникова форма запису комплексного числа
Якщо прийняти як означення показникової функції з уявним показни-
ком формулу Ейлера
def |
|
|
|
||
ei cos i sin , |
|
||||
то ми отримаємо так звану показникову форму комплексного числа: |
|
||||
|
|
|
|
|
|
|
|
|
z r ei |
|
(1.9) |
Якщо розглядати функцію e |
i |
як комплекснозначну функцію дійсного |
|||
|
|
||||
аргументу з областю визначення |
|
, то використання властивостей три- |
|||
гонометричних функцій дійсного аргументу дає наступні властивості показникової функції уявного аргументу:
1. |
e |
i |
|
1 |
|||
|
|
||
2. |
ei 1 |
||
ei 2 |
|||
|
|||
3. |
ei |
||
ei 2 ei( 1 2 )
ei ( 1 2 ) ;
n ei n , n
;
.
10
