Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесская национальная академия пищевых технологий

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ТФКП-15.03.14

.pdf

Скачиваний:

Добавлен:

09.02.2016

Размер:

2.63 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

	e	ln 3	e
		ln 3
sin( i ln 3)			2i
			2i

ln 3

		1
		3 3
		2i
		2i

		4i
		3
		3

2.3.5. Обернені тригонометричні функції

Обернені тригонометричні функції визначаються як функції, обернені

до тригонометричних. Число	w	називається арксинусом	числа	z
(w Arcsin z)			Arcsin z , ско-
, якщо sin w z . Щоб отримати явний вигляд функції			Arcsin z , ско-

ристаємось зв’язком між тригонометричними та показниковою функціями:

	e	i w	e
		i w
z sin w			2i
			2i

i w

e	2i w	2ize	i w

Розв’язуючи це квадратне рівняння відносно

e	i w	i z	1 z	2	iw Ln

Звідси маємо:

e	i w	,

i z

знайдемо
1 z	2	.

Arcsin z i Ln (i z

Аналогічно отримаємо вирази для інших функцій:

1 z	2	) .
	2

обернених

(2.7)

тригонометричних

Arccos z i Ln (z

;

Arctg z

i z

1 i z

i z

Arcctg z

z i

i z 1

z i

i z 1

;

(2.8)

(2.9)

(2.10)

Усі ці функції є нескінченнозначними за рахунок двозначності кореня квадратного та нескінченнозначності логарифма.

Приклад.

Arcsini i Ln ( 2 1) .

Якщо беремо корінь зі знаком «+», то

Arcsini i Ln ( 2 1) i[ln(	2 1) 2k i] 2k
Якщо беремо корінь зі знаком «–», то

i ln(

Arcsin i i Ln (

2 1) i[ln(

2 1) ( 2k )i] (2k 1) i ln(

2 1).

Об’єднавши ці результати, отримаємо остаточно:

Arcsin i k

i ln	2

( 1)	k

2.3.6. Гіперболічні функції

Гіперболічні функції визначаються формулами, аналогічними до відповідних формул для тригонометричних функцій, мають схожі властивості і зв’язані з відповідними тригонометричними функціями певними співвідношеннями. Розглянемо властивості функцій по черзі.

1) Функція	w sh z :
	sh z	ez e z	;	(2.11)
	sh z	2	;	(2.11)
		2

область визначення

D(w)

, область значень

на, непарна, періодична з уявним періодом

відною тригонометричною функцією w sin z :

sin i z

E(w)	, функція однознач-
i . Знайдемо зв’язок з відпо-
i sh z	.

Отже,

2) Функція

ch z

sin iz i sh z

або

sh iz i sin z

	e	z	e	z
ch z	e		e
ch z			2
			2

;

(2.12)

область визначення

D(w)

, область значень

на, парна, періодична з уявним періодом

2 i .

єю w cos z :

cos i z

E(w)	, функція однознач-

Визначимо зв’язок з функці-

ch z	.

Таким чином,

3) Функція

thz

cosiz ch z

або

ch iz cos z

th z	sh z	e2 z 1	;	(2.13)

	ch z	e2 z 1

область визначення D(w)	i		ki,	k	, область значень
область визначення D(w)	\		ki,	k	, область значень
		2
ція однозначна, непарна, періодична з уявним періодом						i ,
кцією w tg z рівністю

E(w)

, функ-

зв’язана з фун-

Остаточно,

4) Функція

i2 z

tgi z

i th z .

tgi z i th z

або

thiz i tgz

w сth z :

			ch z				e	2 z	1
	сth z		ch z				e		1	;
	сth z		sh z				e	2 z	1	;
								2 z

область визначення D(w)	\ ki,	k			,	область
однозначна, непарна, періодична			з	періодом
w ctg z співвідношенням

	(2.14)
значень E(w)	, функція
i	функцією
, зв’язана з	функцією

ctg i z i		ei2 z e i2 z
ctg i z i		2	2
		ei	z e i	z
Отже,
	ctgi z i cth z

i e z ez i cth z . e z ez

або cth i z i ctgz

Якщо взяти будь-яке співвідношення між тригонометричними функціями, замінити аргумент z на i z і скористатися наведеними вище формулами зв’язку між тригонометричними та гіперболічними функціями, то

отримаємо співвідношення між відповідними гіперболічними функціями, наприклад:

cos

z sin

z 1

z sh

z 1,

sin 2z 2sin z cos z

sh2z 2sh z ch z ,

cos2z cos

z sin

ch2z ch

z sh

2.3.7. Обернені гіперболічні функції

Обернені гіперболічні функції визначаються аналогічно оберненим тригонометричним функціям: наприклад, w Arsh z , якщо sh w z . Обернені гіперболічні функції виражаються через логарифмічну функцію:

Arsh z Ln (z

1) .

Arch z Ln (z

;

Arth z

1 z

;

1 z

Arcth z

z 1

Усі ці функції є нескінченнозначними.

Приклад. Обчислити

Arsh i .

Розв’язання.

Arsh i Ln i

(2.15)

(2.16)

(2.17)

(2.18)

2.4. Границя та неперервність функції комплексної змінної

Означення границі функції комплексної змінної повністю аналогічне

відповідному означенню для	функції дійсної змінної.	Нехай функція
w f (z) відображує область D	на область G , і нехай z0	– гранична точка

області при z

D
z	,
0

Комплексне число

z D , якщо 0

w0 ( )

називається

z D : 0

границею функції

	z z	0		f (z)
		0

w
0

f (z)

Приклади. Обчислити границі функцій.

lim

1 ;

z i

2z 2

z (1 i) z (1 i)

lim

z (1 i)

lim

z (1 i)

2i .

z 1 i

Теорема. Для того,

щоб існувала границя функції f (z) u(x, y) iv(x, y)

за умови

z z0

, необхідно і достатньо, щоб існували границі lim u(x, y) та

x x0

y y0

lim v(x, y)

, де (x, y) D

2 .

x x

y y

З цієї теореми випливає, що у теорії функцій комплексної змінної зберігаються результати, справедливі у теорії функцій дійсної змінної: еквівалентність означень границі по Коші та по Гейне, теореми про границі суми, різниці, добутку, частки, складної функції. Аналогічно можна дати означення неперервності функції комплексної змінної.

Функція

w f (z)

називається неперервною у точці

, якщо вона ви-

значена і однозначна у цій точці і деякому її околі і виконується гранична

рівність	lim		f (z) f (z0 ) .
	z z
	z D	0
	z D
Теорема. Для того щоб функція f (z) u(x, y) iv(x, y)					була неперервною у
точці z0	, необхідно і достатньо, щоб неперервні дійсні функції					u(x, y)	і v(x, y)
були неперервні у точці z0 x0				i y0 , причому
			f (z0 ) lim u(x, y) i lim v(x, y) u(x0 , y0 ) i v(x0 , y0 ) .
			z z	z z
			0	0

Ця теорема дає можливість перенести на функції комплексної змінної основні властивості неперервних функцій двох дійсних змінних.

Функція w f (z) , яка задана на множині G і неперервна у кожній точці цієї множини, називається неперервною на множині G . Ми далі розглядатимемо функції, які неперервні в області, у замкненій області або на кривій. Для функцій, неперервних на замкнених обмежених множинах, справедливі властивості, аналогічні до відповідних властивостей функцій дійсної змінної, неперервних на відрізку:

1)кожна функція, неперервна на замкненій множині, є обмеженою;

2)кожна функція, неперервна на замкненій обмеженій множині, досягає

уній своїх найбільшого та найменшого за модулем значень;

3)кожна функція, неперервна на замкненій обмеженій множині, рівномірно неперервна на ній.

2.5. Диференціювання функції комплексної змінної

Похідною функції

w f (z)		по змінній
f (z	) lim w		lim
0		z 0 z	z z0

в точці

f (z) f (z0 ) , z z0

називається границя

(2.19)

якщо границя не залежить від того, як саме точка z прямує до точки	z0 .
Функція f (z) у цьому випадку називається диференційовною у точці	z0 .

Вимога диференційовності накладає дуже важливі умови на поведінку дійсної та уявної частин функції в околі точки (x0 , y0 ) .

Теорема. Для того, щоб функція f (z) u(x, y) iv(x, y) була диференці-

йовною у точці z0 x0 i y0 ,

необхідно і достатньо, щоб функції

u(x, y) та

v(x, y) були диференційовними у точці (x0 , y0 ) ,

і щоб їх частинні похідні по

змінним x, y у цій точці задовольняли умовам

(2.20)

які називаються умовами Коші-Рімана.

Доведення.

Необхідність. За умовою теореми існує границя

lim

f (z) f (z0 )

f (z0 )

z z

z 0

яка не залежить від способу, яким

прямує до нуля. Покладемо спочатку

y 0

, тоді z x і маємо

f (z

) lim

lim

u i v

lim

i lim

, y

) i v

, y

z 0

x 0

x 0 x

x 0

Зараз покладемо x 0 , тоді z i y і

f (z

) lim w

lim u i v

lim u lim

v v

(x , y ) i u

(x , y ).

z 0 z

y 0

i y

i y 0 y

x 0

Прирівнявши ці два вирази для однієї похідної f (z) , отримаємо

u	i	v
x		x

i u

звідки і випливають умови Коші-Рімана (2.20). Достатність. Нехай умови Коші-Рімана (2.20)

функції u(x, y) та v(x, y) диференційовні у точці прирости можна записати у вигляді

виконуються. z0 x0 i y0 , то

Оскільки їх повні

u u(x

x, y

y) u(x

, y

)

y z ,

v v(x

x, y

y) v(x , y

)

y z ,

де

0, 0

при

x 0, y 0 (або

z x i y 0 ). Тоді приріст

функції

w f (z)

дорівнює

f (z0 z) f (z0 ) u i v

y i

z ,

де

i 0

при

z 0

, а доданки у дужках від

не залежать. Поді-

ливши отримане співвідношення на z і зробивши перехід до границі при

умові z 0	, матимемо
	lim	f (z	0	z) f (z	0
			0		0
				z
	z 0			z

що і доводить диференційовність функції

) f

f (z)

(z0 ) ,

у точці

Використовуючи означення похідної від функції комплексної змінної та умови Коші-Рімана, можна отримати наступні еквівалентні формули для

обчислення похідної у точці

z :

f (z)

У полярних координатах умови Коші-Рімана мають вигляд

u	1 v	,	1 u	v
r	r		r	r

(2.21)

і називаються умовами Даламбера-Ейлера.

Однозначна функція w f (z) називається аналітичною у точці z , якщо вона диференційовна у цій точці та деякому її околі. Однозначна функ-

ція w f (z)

називається аналітичною в області G , якщо вона аналітична у

кожній точці цієї області.
Точка z , у якій функція	w f (z)	є аналітичною, називається правиль-

ною (регулярною) точкою цієї функції, усі інші точки називаються особли-

вими (сингулярними) точками.

Приклад. Знайти області диференційованості та аналітичності наступних функцій:

1)	f (z) z	2	;	2)	f (z) z ;	3)	f (z) z z i Im z	2	.
Розв’язання.									u(x, y) x		y		,
1)	Відокремимо дійсну та уявну частини цієї функції:								u(x, y) x	2	y	2	,
										2		2
v (x, y) 2x y . Очевидно, що ці функції є диференційовними на усій компле-

ксній площині. Перевіримо виконання умов Коші-Рімана, для чого знайдемо частинні похідні:

u	2x,	u	2 y,	v	2 y,
x		y		x

Очевидно, що умови Коші-Рімана виконуються для всіх кція є диференційовною, а значить, і аналітичною, на площині.

2)	u x, v y . Знаходимо частинні похідні:
	u	1,	u	0,	v	0,	v	1 .
	x		y		x		y

x та всій

y , тобто функомплексній

Умови (2.20) не виконуються ні при яких значеннях z , тому функція у жодній точці не є диференційовною, а тому і аналітичною.

3)	u x		y	, v 2x y ; частинні похідні дорівнюють
		2	2
				u	2x,	u	2 y,	v	2 y,	v	2x .
				x	2x,	y	2 y,	x	2 y,	y	2x .
				x		y		x		y

Друга з умов (2.20) виконується тотожно (при будь-яких y ), а перша – тільки при x 0 , тому функція є диференційовною тільки на уявній осі і у жодній точці не є аналітичною.

2.6. Інтеграл від функції комплексній змінній

2.6.1. Лінії на комплексній площині

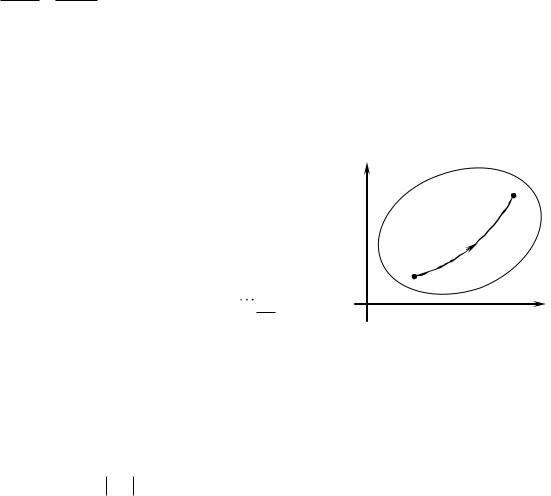
Як відомо, кожному комплексному числу z x i y відповідає точка z(x , y) на комплексній площині. Рухаючись по комплексній площині, точка описує деяку лінію. Рівняння цієї лінії може бути записане в різних формах.

1)Явне рівняння лінії: y y(x), r r( ) ;

2)Параметричні рівняння лінії: z z(t) x x(t), y y(t) . Приклади.

y x

– рівняння параболи;

x x

y y

– рівняння прямої, яка проходить через точки z1 x1

та

;

z z

R ei ,

0 2

– рівняння кола радіуса R з центром у точці

i y0

. Це рівняння також може бути записане у еквівалентному ви-

гляді

z z0

R .

2.6.2. Означення та властивості інтеграла

Нехай в області

D комплексної площини

задано неперервну функцію

f (z) u(x, y) i v(x, y)

, і

нехай

– кусково-гладка крива з початком у

точці

та кінцем у точці z , яка цілком лежить в

області

. Довільним чином розіб’ємо криву

на

часткових дуг точками

z0 , z1, z2

, zn 1, zn z

і позначимо

zk 1

zk xk

i yk ,

k 1, n . На

кожній частковій дузі

k виберемо довільну точку k

i k

і складемо

інтегральну суму

Sn f ( k ) zk u( k , k ) iv( k , k ) xk i yk

k 1

[u( k , k ) xk v( k , k ) yk ] i [v( k , k ) xk u( k , k ) yk ].

Позначимо

k 1

на

max

k і будемо розглядати різні розбиття кривої

1 k n

часткові дуги

k за умови 0 , і значення інтегральних сум, що їм від-

повідають. Якщо при цьому існує скінченна границя послідовності інтег-

ральних сум	Sn , то ця границя називається інтегралом від функції f (z)
вздовж кривій , тобто справедлива рівність
		n
	f (z)dz lim f ( k ) zk .		(2.22)
		0 k 1

Якщо записати функцію шеться у вигляді



f (z) в алгебраїчній формі, то рівність (2.22) запи-

f (z)dz	udx vdy i	vdx udy .	(2.22')
f (z)dz	udx vdy i	vdx udy .	(2.22')

Таким чином, інтеграл від функції комплексної змінної вздовж кривої виражається через криволінійні інтеграли другого роду від дійсних функцій u u(x, y) та v v(x, y) . Для існування інтеграла від функції комплексної змінної достатньо неперервності підінтегральної функції і не є необхідною її диференційовність або аналітичність.

З означення інтеграла випливають його властивості:

1)
1)

f(z)dz

f (z)dz

, де

– крива

, яку проходять у протилежному

напрямі;

2)		f (z)
2)		f (z)

3)		a f (z)
3)		a f (z)

4)	f (z) dz

g(z) dz		f (z)dz		g (z)dz	;
g(z) dz		f (z)dz		g (z)dz	;

dz a	f (z) dz,		a	;
dz a	f (z) dz,		a	;

f (z) dz f (z) dz,				1 2 ;
1		2

5) f (z) dz	f (z) dz M L ,	M max f (z) ,	L

– довжина дуги кривої .

Спосіб обчислення інтеграла від функції комплексної змінної залежить від способу завдання рівняння лінії інтегрування . Якщо рівняння задане в

явному вигляді y y(x) , то інтеграл обчислюється за формулою (2.22'). що ж рівняння лінії задане у параметричному вигляді z z(t), t

Як-

то, виконавши під знаком інтеграла заміну змінної, отримаємо формулу для обчислення інтеграла у вигляді



f(z) dz

f [z(t)]z (t)dt

(2.23)

Приклад. Обчислити інтеграли вздовж заданих ліній.

1)
1)

z	2	dz,

:	y x,	z	0,	z	2	1 i.
		1			2

	Розв’язання.

	z	2dz			(x iy)2					(dx idy)						(x2			iy2 )	2ixy	(dx idy)		(x2 y2 )dx 2xydy

													1								1				1

i			(x2	y2 )dy 2xydx										(x2		x2 ) 2xx dx i					(x2	x2 )	2xx dx	2		x2dx
													0								0				0
			1				x	3	1		x	3	1		2		2
2i x				dx		2	x			2i	x				2		2	i.
			2
			0				3		0		3		0		3		3
			0						0				0

Другий спосіб обчислення

прямої у вигляді

i / 4

z r e

dz e

z 2dz r2e

dr e

r 2dr

z z0

R .

z z

інтегралу: запишемо параметричне рівняння

/ 4	dr,			z r e			i / 4		,	0 r		2.
	dr,			z r e					,	0 r		2.
		i			r3						i
		i				2		2 2			i				2	2
e								2 2					i sin		2	2	i .
			4							e	4 cos
			4							e	4 cos
			3			0		3				4		4	3	3

Розв’язання.

iRe

z z0 R e

dz iRe

d ,

i d 2 i

z z

R e

3) Re z dz,

z R,

0 arg z .

Розв’язання.

– не залежить від

																				d
Re z dz R cos R( sin i cos ) d R										sin cos d iR						cos				d
									2						2			2
			0							0						0
	R	2		iR	2	R	2					iR	2	sin 2							i R	2
		2			2		2						2									2
			sin 2d		(1 cos 2)d			cos 2														.
	2		sin 2d	2	(1 cos 2)d	4		cos 2				2		2							2	.
	2		0	2	0	4					0	2		2					0		2
2.6.3. Інтегрування аналітичних функцій
Очевидно, що в загальному випадку інтеграл f (z)dz																залежить як від

підінтегральної функції f (z) , так і від кривої інтегрування																	. Далі ми бу-

демо найчастіше розглядати інтеграли від функцій, аналітичних у деякій обмеженій області, причому кривою інтегрування є кусково-гладка крива, яка не має само перетинів. Якщо ця крива замкнена, то вона називається

замкненим контуром, а інтеграл – контурним інтегралом і позначається

символом		f (z) d z .
символом		f (z) d z .

Можна довести, що якщо функція	f (z) ана-
літична в однозв’язній області D , то	інтеграл

вздовж будь-якої кусково-гладкої кривої, яка ці-

лком лежить всередині області	D , залежить ли-
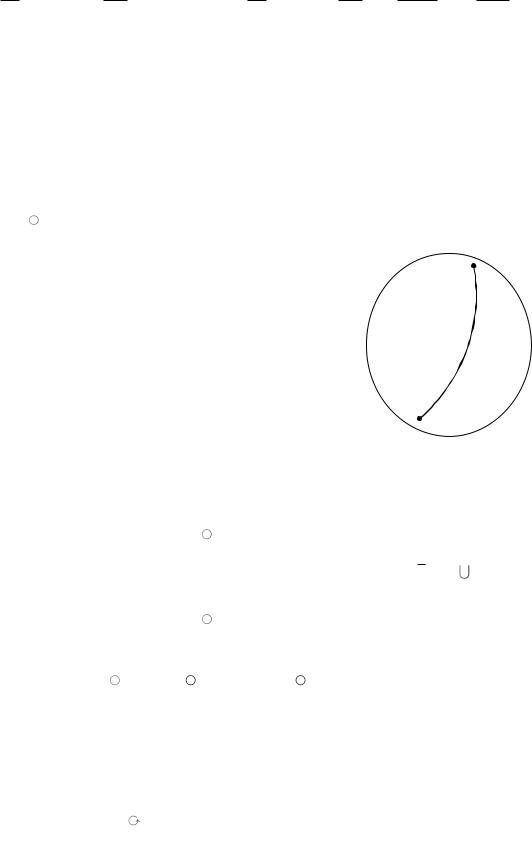
ше від положення початкової z1	і кінцевої	z2	то-
чок цієї кривої, тобто справедлива рівність

	z2
f (z) dz f (z) dz .
	z1

Теорема Коші. Якщо функція f (z) аналітична в однозв’язній області D , то інтеграл від цієї функції по будь-якому замкненому контуру C , що цілком лежить в області D , дорівнює нулю, тобто справедлива рівність

f (z) dz 0 .

Якщо, крім цього, функція неперервна у замкненій області межа області, то

D D

, де

–



f (z) dz

Доведення. Згідно з формулою (2.22) запишемо

f (z) dz u dx v d y i v dx u d y .

C	C	C
Оскільки функція f (z)	аналітична всередині контуру		C , то функції	u (x, y)

та v (x, y) мають там неперервні частинні похідні першого порядку. З цього випливає, що до криволінійних інтегралів у правій частині рівності можна застосувати формулу Гріна:

	Fy		F
	Fxdx Fy dy		x dxdy ,
		x
C	D		y

де D – область, яка обмежена контуром C . Тоді матимемо

	v	u		u
f (z)dz	x	dxdy i		x
D	x	y	D	x

v dxdyy

Оскільки підінтегральна функція аналітична, для неї виконуються умови Коші-Рімана, тому інтеграли у правій частині дорівнюють нулю, і

	f (z) d z 0 .	(2.24)
C

Аналогічно може бути доведене друге твердження теореми.

Узагальнимо теорему Коші на випадок многозв’язної області. Додатним напрямом обходу межі області вважатимемо такий напрям руху, при якому область весь час залишається ліворуч.

Теорема. Нехай функція яка обмежена зовні контуром

	c
	3
f (z)	аналітична у багатозв’язній області
,	а зсередини – контурами 1,	2 ,	, n ,

D ,

та

неперервна на всій межі. Тоді інтеграл від функції wобласті D , яка складається з зовнішнього контуру

(z)	по повній межі

і внутрішніх кон-

турів

2 ,

, n

Доведення.

і яку проходять у додатному напрямі, дорівнює нулю.

Проведемо розрізи

c1,

c2 ,

, cn

, які з’єднують зовнішній

контур

з внутрішніми контурами

	1	,		2	,
	1			2

,	n

, і позначимо через за-

мкнений контур, котрий складається з контуру

і розрізів

c	,	c	2	,	, c	n
1			2			n

(причому у кожному розрізі необхідно розрізняти два береги). Область, яка обмежена контуром , є однозв’язною, тому за теоремою Коші



f (z) dz

Оскільки кожний з розрізів

c1,

c2 ,

двічі у протилежних напрямах (по му з розрізів взаємно знищуються.

, cn

при обході контуру

проходиться

різних берегах), то інтеграли по кожноЗвідси маємо рівність

f (z) d z f (z) d z		f (z) d z 0 ,
	1	n
де зовнішній контур	проходиться проти ходу годинникової стрілки, а

внутрішні контури 1, 2 , , n – за ходом годинникової стрілки. Змінивши

напрям обходу внутрішніх контурів на протилежний (проти ходу годинникової стрілки) і, відповідно, знаки перед цими інтегралами, отримаємо

	f (z) d z	f (z) d z	f (z) d z	f (z) d z ,	(2.25)
	1	2		n

де всі контури обходяться проти ходу годинникової стрілки. Таким чином, ми отримали друге формулювання теореми Коші для багатозв’язної області.

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.02.201615.28 Кб51титулка отчет орг. практика ОНАПТ 2015.docx
#
11.09.2019181.76 Кб6титульный и прочее-1.doc
#
17.07.201994.21 Кб1Трансп,енергет,ремонт.doc
#
15.11.2018291.33 Кб12ТТЖП Мясо(метод.).doc
#
15.11.2018461.31 Кб20ТТЖП Рыба(метод.).doc
#
09.02.20162.63 Mб17ТФКП-15.03.14.pdf
#
09.02.2016727.04 Кб71ТХПП МЕТОДИЧКА.doc
#
09.02.20161.73 Mб80Тюнинг двигателей.doc
#
09.02.2016222.6 Кб9УЗРГ.docx
#
04.12.201881.76 Кб17УИРС.docx
#
09.02.2016350.5 Кб29Укр культура.docx