Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесская национальная академия пищевых технологий

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ТФКП-15.03.14

.pdf

Скачиваний:

Добавлен:

09.02.2016

Размер:

2.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 94 5 6 7 8 9 > Следующая >>>

Теорема. Якщо функція	f (z) аналітична у багатозв’язній області D і
неперервна на повній межі	цієї області, то інтеграл по контуру, що об-

межує область зовні, дорівнює сумі інтегралів по всім контурам, що обмежують область зсередини (при цьому всі контури необхідно обходити або за ходом годинникової стрілки, або проти).

Наприклад, якщо функція f (z) аналітична у кільці між двома замкне-

ними контурами

	1

	2

та неперервна на самих контурах, то

	f (z) d z		f (z) d z .

1		2

Приклад. Обчислити інтеграл

I	dz			,	n
	(z z	)	n

	0

вздовж довільного

замкненого контуру. Розв’язання. Якщо точка

лежить поза областю D , яка обмежена

контуром

, то підінтегральна функція	f (z)	1		аналітична в області

		(z z	)n
		0

D і, за теоремою Коші, I 0 . Якщо ж точка z0	належить до області D , то
проведемо коло C радіуса R з центром у точці	z0 , яке не перетинає конту-
	i	,
ру . Рівняння такого кола у комплексній формі має вигляд z z0 R e

тоді	d z iR e	i	d

між контурами



. Підінтегральна функція	f (z)	1		аналітична у кільці

		(z z	)n
		0

і C , тому

Якщо

e	2 i(1 n)	e	0
	2 i(1 n)		0

d z

iR e

i(1 n)

d .

(z z

)

(z z

)

n 1

, то

I i

d 2 i

якщо

n 1

, то врахувавши рівність

, отримаємо

i (1 n)

0 .

n 1

i (1

Остаточно, для цілих n маємо

	dz			n 1,
I			0,	n 1,
I	(z z0 )	n		n 1.
	(z z0 )		2i,	n 1.
З теореми Коші випливає, що інтеграл від функції					f (z) , яка аналітична

у однозв’язній області D , взятий від фіксованої точки z0 до довільної точ-

ки z , не залежить від кривої інтегрування, що з’єднує ці точки і цілком лежить в області D , і є однозначною функцією z :

z
(z)	f ( ) d
z
0

Властивості цієї функції визначає наступна

Теорема. Якщо функція f (z) аналітична в області D , то і функція (z) також аналітична у цій області, причому (z) f (z) .

Доведення. За означенням похідної

	(z) lim	(z z) (z)
	(z) lim	z
	z 0	z

Доведемо справедливість рівності

	lim	(z z) (z)
		z
	z 0

f (z)

Для цього оцінимо вираз

(z z) (z)

z z

f (z)

f ( )d f ( )d f (z) z

z z

f ( )d

f ( )d f (z)

z z

f ( ) f (z) d

max

f ( ) f (z) z

max

f ( ) f (z) .

[ z, z z ]

[ z, z z]

Тоді

	lim	(z z) (z)
		z
	z 0

f (z) lim	max	f ( )
z 0	[ z , z z ]

(z)

оскільки функція

f (z)

неперервна в точці

. Теорему доведено.

Це означає, що функція

(z)

є первісною функції

Множина всіх первісних даної функції f (z)	називається
тегралом від даної функції і позначається

(z) в області D .

невизначеним ін-

де

F(z)

f (z) d z

– будь-яка первісна функції

F(z) (z) ,

C C

– комплексна константа. Для

інтеграла від аналітичної функції комплексної змінної вірна формула Нью- тона-Лейбніца:

z2	z2
f (z) d z F (z)
z1	z1

F (z2 ) F (z1 ) .

Для обчислення невизначених інтегралів від функцій комплексної змінної використовуються відомі методи заміни змінної та інтегрування по частинам, таблиця невизначених інтегралів в обох випадках також однакова.

Приклади:

						z	n 1
z	dz e	z	C ;	n	d z	z	C ;	(n 1);
e	dz e		C ;	z	d z		C ;	(n 1);
						n	1

		d z
		z
		z

ln z C

Оскільки первісна повинна бути аналітичною функцію, це накладає певні обмеження на області, в яких справедливі наведені формули. Перша формула та друга при n 0 вірні на всій комплексній площині; друга формула n 0 вірна у будь-якій області, що не містить точку z 0 ; третя формула справедлива для всіх z крім тих, що лежать на від’ємній частині дійсної вісі z x 0 , і так далі.

Приклад. Обчислити інтеграл I (z2 2i z) d z .

Розв’язання. Легко пересвідчитись, що підінтегральна функція аналітична. Тому

i		z		3
I (z	2	2iz) d z			i z	2
I (z		2iz) d z	3		i z
0			3

2.6.4. Інтегральна формула Коші

1 i i 3

	2	i
	3	i
	3

Теорема. Нехай функція

f (z) аналітична в однозв’язній області

D , яка

обмежена кусково-гладким контуром , і неперервна на цьому контурі.

Тоді для будь-якої точки z0 , що лежить всередині області	D , справедлива
формула

	f (z0 )	1
		2 i

f (z)
z z	0

(2.26)

яка називається формулою Коші. Доведення. Підінтегральна функція

f (z)
z z	0

аналітична всюди в області

D , виключаючи точку z0 . Оточимо точку z0 колом C з центром у цій точці

і радіусом r настільки малим, щоб коло не перетиналося з контуром . Оскільки підінтегральна функція аналітична в кільці між контурами і C , то, за теоремою Коші для многозв’язної області, маємо

f(z)

z z0 C

f (z)
z z	0

Скориставшись розглянутим раніше прикладом на сторінці 27, запишемо

f (z0 )

2 i f (z

)

z z

2 i

z z

2 i

і оцінимо різницю

f (z)

d z

f (z0 )

f (z) f (z

)

d z

f (z) f (z

)

d z

2 i

z z

max f (z)

f (z

) 2 r max

f (z) f (z

) .

2 r

z C

Вибравши

радіус

кола

достатньо

малим,

можна

зробити різницю

f (z) f (z0 )

як завгодно малою,

оскільки функція

f (z) неперервна; почат-

ковий вираз, що оцінюється,

від r

взагалі не залежить,

тому він дорівнює

нулю.

Таким чином, значення аналітичної функції у внутрішніх точках області повністю визначаються її значеннями на межі області. Інтеграл, що стоїть у правій частині формули Коші (2.26), називається інтегралом Коші, і

його можна обчислити за формулою

f (z)

d z 2 i f (z0 ) .

(2.26')

z z

Наслідок. Якщо функція

f (z)

аналітична в області

D , яка обмежена

кусково-гладким контуром , і неперервна на замкненій області

D , то у

будь-якій точці z0 цієї області функція

f (z) диференційовна скільки за-

вгодно раз, причому

f (n) (z0 )

f (z)

d z .

(2.27)

2 i

(z z

)n 1

Доведення. Для n 1

маємо

f (z0 ) lim

f (z

z) f (z

)

lim

f (z) d z

z z0

z 0

z 2 i

z z0 z

2 i

lim

z z

f (z) d z

lim

f (z) d z

2 i

(z z

z)(z z

2 i

(z z

z)(z z

z 0

)

z 0

)

f (z) d z

2 i

(z z

)

2 .

Аналогічно формула (2.27) ном, з аналітичності функції f (z

може бути доведена для n 2 . Таким чи- ) у деякій точці z випливає, що вона у цій

точці має похідні всіх порядків, і ці похідні також аналітичні в точці

z .

Формула (2.27) може використовуватись для обчислення деяких кон-

турних інтегралів, коли записати її у вигляді

f (z)

d z

2 i

f (n) (z0 ) .

(2.27')

(z z

)n 1

Приклад 1. Обчислити інтеграл

d z

z 2i 1

Розв’язання. Перепишемо інтеграл у вигляді

d z

(z 2i)(z 2i)

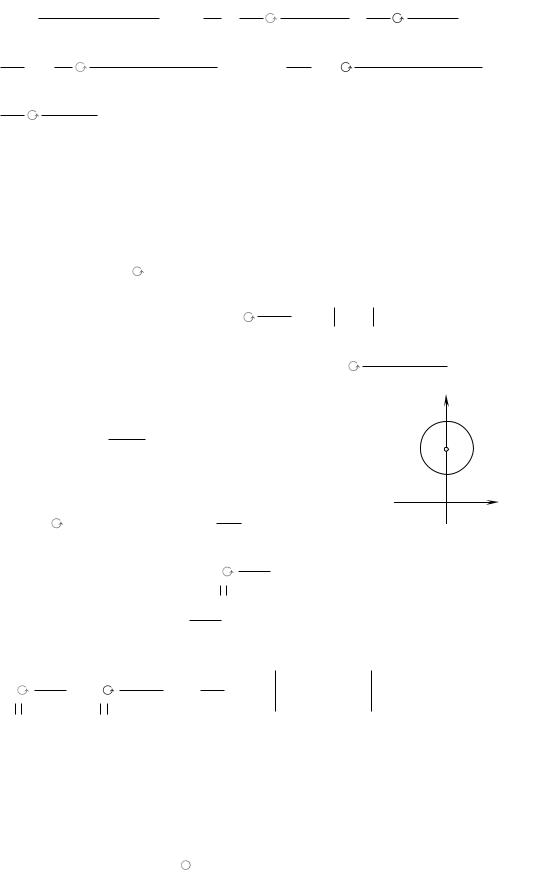
Контур є колом радіуса

R 1 з центром у точці

2i . Функція

f (z)

аналітична всередині кола.

z 2i

Тоді з формули (2.26') маємо

	1

I	z 2i		1
		dz 2 i
	z 2i
	z 2i		2i 2i

Приклад 2. Обчислити інтеграл

2 i .

4i 2

	cos z		dz
	z	3
z 1

Розв’язання. Функція

f (z)

cos z

аналітична всюди в крузі

точки

. Тоді за формулою (2.27') матимемо

cos z

d z

2 i

(cos z)

i cos z

i .

(z 0)

z 1

z 0

, крім

На завершення розділу сформулюємо без доведення декілька важливих теорем, що використовуються у диференціальному численні функцій

комплексної змінної.
Теорема Морера (обернена до теореми Коші). Якщо функція	f (z) непе-
рервна в однозв’язній області D і для будь-якого замкненого	кусково-
гладкого контуру D справедлива умова
f (z) d z 0 ,

то функція f (z) аналітична всюди в області D .

Теорема Ліувілля. Якщо функція

f (z)

аналітична і обмежена на всій

комплексній площині, то вона постійна. Теорема про середнє. Якщо функція

f (z)

аналітична в області

, і

–

круг, що міститься у цій області, то значення функції у центрі круга дорівнює середньому значень функції на колі – межі цього круга:

	f (z0 )	1		f (z) d z .

		2 z z0		R
Принцип максимуму модуля. Якщо функція f (z) , яка не є постійною,
аналітична в області	D , то її модуль		f (z) не може досягати свого макси-

мального значення в жодній внутрішній точці області D .

Теорема. Якщо функція	f (t) неперервна на межі області D , то фун-
кція, що задана інтегралом Коші
	(z)	1	f (t) d t	,

		2 i	t z

аналітична всюди в цій області.

2.6.5. Визначення аналітичної функції за її дійсною частиною

Дійсна функція u(x, y)

дійсних змінних

y, що однозначна в області

, має неперервні частинні похідні другого порядку і задовольняє рівнянню

	u			u
2			2
x		2	y		2

(2.28)

називається гармонічною функцією. Диференціальне рівняння у частинних похідних (2.28) називається рівнянням Лапласа, а диференціальний оператор

			2			2
			2			2
	x			2	y		2
	x			2	y		2
– оператором Лапласа.
У попередньому розділі було показано, що аналітична в області								D
функція f (z) комплексної змінної	z	у кожній точці цієї області має похідні

всіх порядків. Зокрема, її похідну першого порядку можна записати у вигляді

			u	i	v	i	u	v
								.
		f (z)	x		x		y	.
			x		x		y	y
Оскільки		сама є аналітичною функцією в області							D	, то з попередньої
Оскільки	f (z)	сама є аналітичною функцією в області								, то з попередньої

рівності випливає, що існують частинні похідні

	u				u			u
2				2			2
x		2	,	x y		,	y x		,
x				x y			y x

причому всюди в області D

	u
2
x y
x y

	u
2
y			,
	2
		u
2
y x

	v						v						v			v
2						2						2			2
x		2	,						,		y x			,	y		2	,
x					x y						y x				y

				2	v					2	v
				2						2
												.
	x y							y x

(2.29)

З аналітичності функції f (z) в області D випливає, що виконуються умови Коші-Рімана (2.20). Якщо продиференціювати першу рівність по x ,

а другу – по y , а потім додати їх, то в силу рівностей (2.29) отримаємо, щоu 0 . Аналогічно одержимо рівність v 0 .

Таким чином, дійсна u(x, y) та уявна v(x, y) частини аналітичної в області D функції f (z) є гармонічними функціями. Функцію v(x, y) назива-

ють гармонічно спряженою з функцією u(x, y) .

Припустимо зараз, що в однозв’язній області D задана гармонічна функція u(x, y) . Тоді функція v(x, y) , гармонічно спряжена з u(x, y) , може дуже просто бути виражена через неї. Дійсно, з умов Коші-Рімана маємо

	d v	u	d x	u	d y
	d v		d x		d y
		y		x	.
		y		x
Оскільки u 0	, то права частина є повним диференціалом, тому

( x, y )			u
v(x, y)				dx
			y
( x	, y	)

0	0

	u	d y
	x	d y
	x

де (x0 , y0 ) – фіксована точка області D , C – довільна дійсна стала, а інтеграл не залежить від шляху інтегрування.

Таким чином,	аналітична в однозв’язній області	D функція	f (z) за її
дійсною частиною	u(x, y) визначається з точністю до адитивної довільної
уявної сталої i C за співвідношенням

( x, y )			u
f (z) u(x, y) i				dx
			y
( x	, y	)
0	0

	u	d y i C
	x	d y i C
	x

(2.30)

Аналогічно ласті D функції

можна отримати вираз для f (z) за її уявною частиною

аналітичної в однозв’язної об-

v(x, y) :

( x, y )			v
f (z)				dx
			y
( x	, y	)
0	0

	v	d y
	x	d y
	x

iv(x, y) C

(2.31)

Приклад. За дійсною частиною	u(x, y) x	2	y	2	x	аналітичної функції

f (z) знайти саму функцію.

Розв’язання. Скористаємось формулою (2.30) і обчислимо інтеграл від

точки (0, 0) до точки	(x, y)	вздовж ламаної лінії, перша ланка якої – відрі-
зок прямої від точки	(0, 0)	до точки	( x, 0) , друга – відрізок прямої від точки
( x, 0) до точки (x, y) :
x		y
f (z) x2 y2 x i (2 0)dx i (2x 1)d y i C x2 y2 x i (2xy y) i C
0		0
(x2 2xyi y2 ) (x i y) Ci z2			z C .

3. Ряди аналітичних функцій і ізольовані особливі точки

Розклад функцій в ряди має не тільки теоретичний, але й практичний аспекти. Для практики важливо, що за допомогою рядів можна розв’язувати такі задачі, як обчислення значення функцій, знаходження наближеного розв’язку диференціальних рівнянь у багатьох задачах прикладного характеру, обчислення деяких визначених інтегралів і таке інше. Для теорії істотно, що кожну аналітичну функцію можна в околі кожної точки розглядати, як представлену у вигляді суми степеневого ряду.

3.1. Числові та степеневі ряди

Теорія рядів з комплексними членами, як числових, так і функціональних, будується аналогічно тому, як це робиться у дійсному аналізі. Залишаються без зміни такі поняття, як сума ряду, умовна, абсолютна та рівномірна збіжність, область збіжності і так далі. Питання про збіжність рядів з комплексними членами може бути зведене до задачі про збіжність рядів з дійсними членами за допомогою наступної теореми.

Теорема. Для збіжності ряду з комплексними членами

i y

n 1

необхідно і достатньо, щоб збігалися два ряди з дійсними членами

xn

n 1

і yn

n 1

Зупинимось детальніше на вивченні степеневих рядів, тобто рядів вигляду

	(z z		n	c	c (z z		)	c	(z z		n
c		)	n							)	n	,
c		)								)		,
n	0			0	1	0		n	0
n 0

(3.1)

де

– фіксована точка комплексної площини,

– комплексні сталі числа

(коефіцієнти ряду). У теорії степеневих рядів дуже важливе значення має Теорема Абеля. Якщо степеневий ряд (3.1) збігається у деякій точці

z z0		, то він збігається абсолютно в кожній точці z , яка задовольняє умові
	z z0		z z0	, і рівномірно збігається у замкненому крузі z z0 z z0 .

Доводиться теорема Абеля аналогічно тому, як це було для степеневих рядів з дійсними членами. Перелічимо основні властивості степеневих рядів.


1. Якщо ряд (3.1) розбігається у деякій точці z	*	, то він розбігається в
1. Якщо ряд (3.1) розбігається у деякій точці z		, то він розбігається в
кожній точці z , яка задовольняє умові z z0			z	*	z0 .

2.Якщо область збіжності степеневого ряду не вироджується в точку z z0 і не співпадає з усією комплексною площиною, то існує таке

число

, що всередині круга z z0 R ряд збігається абсолют-

но, а зовні цього круга ряд розбігається. Цей круг називається кругом збіжності степеневого ряду, а число R – його радіусом збіжності. У замкненому крузі z z0 R ряд (3.1) збігається рівно-

мірно.

3. Всередині круга збіжності степеневий ряд збігається до аналітичної функції f (z) .

4.Степеневий ряд всередині круга збіжності можна диференціювати

іінтегрувати будь-яке число разів, причому радіус збіжності отриманих рядів дорівнює радіусу збіжності вихідного ряду.

5.Радіус збіжності степеневого ряду (3.1) можна знайти за формулами

R lim	c
	n

n c		1
	n

або

R	1
R
	lim n	c
	n	n
	n

Цей радіус дорівнює відстані від точки	z0	до найближчої особли-
вої точки функції f (z) .

Відомо, що вираз 1 q q	2		q	n		– це ряд, членами якого є члени

нескінченної геометричної прогресії (геометричний ряд). У випадку, коли

1	, ряд збігається, і його сума дорівнює
	, ряд збігається, і його сума дорівнює
	1	1	q q	2	q	n
		1	q q		q

	1 q

1 1 q

, тобто має місце рівність

q 1	.

Відповідно, степеневий ряд

		1 x x		x
x	n	1 x x	2	x	n
	n		2		n
n 0

є геометричним рядом, областю збіжності якого є інтервал	x

властивостями рядів геометричний ряд з комплексною змінною

. Згідно з

		1 z z		z
z	n	1 z z	2	z	n
	n		2		n
n 0

збігається абсолютно всередині кола радіуса

R 1

з центром у точці


z 0		z	1

і сума його дорівнює 1 . Аналогічно можна знайти суму та

1 z

область збіжності наступних степеневих рядів:

1)		1	1 z z2											( 1)n zn					;	z 1;


1 z
2)		1				1	z2 z4								z2n				; z 1;

		z2
1		z2
3)		1			1		z2				z4				( 1)n z2n					; z 1;

		z2
1		z2
		z						1					1		1				1
4)		z						1		1			1		1				1	; z 1;
4)	z 1								n	1					2				n	; z 1;
	z 1					n 0 z							z		z				z
		z z0											1
5)		z z0											1				;	z z0 1.
5)	(z z					)						(z z			)	n	;	z z0 1.
	(z z					)	1				n 0	(z z			)
				0							n 0		0
3.2. Ряди Тейлора та Маклорена
Нехай у точці z0													та деякому її околі визначено аналітичну функцію f (z) .
Ряд вигляду

	)	f (z	)	(z z	)
f (z	)	0		(z z	)
0		1!		0
		1!

називається рядом Тейлора функції випадок ряду Тейлора

(z)

(n)		)
(z	0	)	(z
	0
n!
n!

Якщо

z	)	n		(3.2)
		n
0
z0 0			, то маємо окремий

f (0)

(n)

(0)

f (0)

(3.3)

який називається рядом Маклорена.

Формули для коефіцієнтів ряду Тейлора (Маклорена) у випадку комплексної змінної мають той же самий вигляд, що у випадку рядів з дійсними членами

c	1	f (n) (z		) .	(3.4)
			0
n	n!

Якщо скористатися для похідних аналітичної функції інтегральною формулою Коші (2.27), то для коефіцієнтів ряду Тейлора отримаємо:

c		1					f (z) dz
	n	2 i					(z z	)	n 1 .

				z z		r R
					0		0
Теорема Коші. Функція	f (z)		, яка аналітична у крузі

z z	0

(3.4')

, може бу-

ти єдиним способом розкладена у ньому в ряд Тейлора. У будь-якій замкненій області, що лежить у цьому крузі, ряд Тейлора збігається рівномірно.

Приклад. Розкласти функцію	f (z) z	4	в ряд Тейлора в околі точки z0


Розв’язання. Знаходимо значення функції та її похідних у точці				z0

i .

i :

f (z) z

f (i) 1;

(z) 4z ,

f (i) 4i;

(z) 12z

f (i) 12;

f (z) 24z,

f (i) 24i;

(4)

(z) 24,

(4)

(i) 24;

1 4i(z

i) 6(z i)

4i(z i)

Оскільки формули обчислення коефіцієнтів ряду Тейлора,

а також

формули диференціювання однакові для функцій дійсної змінної

та ком-

плексної змінної

z , то і ряди Тейлора для цих функцій також мають одна-

ковий вигляд, наприклад:

ez 1

( 1)n

z2n 1

sin z z

(2n 1)!

cos z 1

( 1)n

z2n

(2n)!

z2n 1

sh z z

(2n

1)!

ch z 1

z2n

(2n)!

Областю збіжності цих рядів є вся комплексна площина. Необхідно зазначити, що ряди

ln(1 z) z

( 1)

n 1

1 z

( 1)

( 1)( 2)

(1 z)

збігаються всередині круга радіуса

R 1

з центром у точці

Приклади. Знайти області збіжності рядів:

z (1

;

n 2

n 0

n 1

Розв’язання.

1) Знайдемо радіус збіжності:

R lim

lim

n! (n 1)

n 1

(n 1)!

n c

Отже, областю збіжності даного ряду є вся комплексна площина.

2) Оскільки

c	1		,	c				1
c		n	,	c						n 1
n	n 2	n		n 1		(n 1) 2				n 1
	n 2					(n 1) 2
					(n 1) 2			n	2
								n
	R lim
	R lim					n 2	n
			n				n
			n

,	то

lim		2(n 1)
		n
n

Таким чином, ряд збігається всередині круга

z (1 i) 2	або (x 1)	2	(y 1)	2
	або (x 1)		(y 1)

3.3. Ряд Лорана

Ряди Тейлора – апарат, зручний для представлення функцій, аналітичних в кругових областях. Але часто виникає потреба в апараті для представлення функцій, аналітичних в областях іншого вигляду. Наприклад, при вивченні функцій, аналітичних у деякому околі точки z0 всюди, крім самої

точки

z	0

, приходиться розглядати області

0 z z	0	R	,

або, у більш загальному випадку, області вигляду

r	z z	0	R,	r 0,
		0

Для дослідження такого роду аналітичних функцій використовуються ряди вигляду

	(z z0 )						c n	n ,	(3.5)
f (z) cn	(z z0 )	n	cn (z z0 )	n				n ,	(3.5)
		n		n
n			n 0			n 1	(z z )
n			n 0			n 1	0
де z0 – фіксована точка комплексної площини, c					n	– задані комплексні числа
					n

(коефіцієнти ряду). Цей ряд називається рядом Лорана, перший доданок у правій частині рівності називається правильною або регулярною частиною ряду, другий доданок – головною або сингулярною частиною ряду Лорана. Правильна частина є звичайним степеневим рядом, який збігається всередині круга z z0 R до деякої аналітичної функції комплексної змінної

<<< < Предыдущая 1 2 34 / 94 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.02.201615.28 Кб51титулка отчет орг. практика ОНАПТ 2015.docx
#
11.09.2019181.76 Кб6титульный и прочее-1.doc
#
17.07.201994.21 Кб1Трансп,енергет,ремонт.doc
#
15.11.2018291.33 Кб12ТТЖП Мясо(метод.).doc
#
15.11.2018461.31 Кб20ТТЖП Рыба(метод.).doc
#
09.02.20162.63 Mб17ТФКП-15.03.14.pdf
#
09.02.2016727.04 Кб71ТХПП МЕТОДИЧКА.doc
#
09.02.20161.73 Mб80Тюнинг двигателей.doc
#
09.02.2016222.6 Кб9УЗРГ.docx
#
04.12.201881.76 Кб17УИРС.docx
#
09.02.2016350.5 Кб29Укр культура.docx