
ТФКП-15.03.14
.pdf
Тоді
z |
z |
|
r r |
e |
i ( |
|
) |
; |
z |
|
r |
i ( |
|
) |
. |
||
2 |
1 |
2 |
|
|
1 |
1 e |
1 |
2 |
|
||||||||
1 |
|
1 |
2 |
|
|
|
|
|
z |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
(1.10)
Приклад. Знайти у показниковій формі добуток
z1 |
3 i , z2 1 3 i . |
|
|
Розв’язання. Знайдемо модулі та аргументи чисел |
z1 |
та запишемо їх у показниковій формі:
і

 3
3
частку
i |
і z2 |
чисел
1 |
3i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
r |
|
( |
|
3) |
2, |
arctg |
|
|
|
|
|
z |
2 e |
6 , |
|
|
|
|
|||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
6 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
i |
2 |
|||
r |
|
(1) |
2 |
( |
3) |
2 |
2, |
|
arctg |
|
|
|
z |
|
2 e |
3 . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тоді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
i |
|
|
|
z |
|
2 |
|
i |
6 |
|
|
|
|
|
i |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
z z |
|
2 2 e |
6 3 |
4 e |
|
|
6 ; |
|
|
1 |
|
|
|
e |
|
|
3 |
1 e |
|
. |
||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тригонометрична та показникова форми запису комплексного числа зручні для виконання операцій піднесення комплексного числа до натурального степеня та добування кореня з комплексного числа.
1.3.4. Піднесення до степеня комплексного числа
Натуральний степінь |
n |
комплексного числа |
z |
||
ток n співмножників, кожний з яких дорівнює z : |
|
||||
|
z |
n |
z z |
z , n . |
|
|
|
|
|
|
|
|
|
|
n |
|
|
визначається як добу-
Використовуючи правила множення комплексних чисел у тригонометричній та показниковій формах, матимемо
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
i |
z |
n |
|
|
r (cos i sin ) |
n |
r |
n |
(cosn i sin n ) |
|
|||||
|
|
w e |
|
|
|
|
|
||||||||||
тобто |
n |
, n . Остаточно |
|
|
|
|
|
|
|
|
|||||||
r |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
z |
n |
n |
(cosn isin n ) . |
|
|||||||
|
|
|
|
|
|
|
r |
|
|||||||||
У показниковій формі ця формула має вигляд |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
z |
n |
n |
i n |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r e |
|
|
|
|||
Формула (1.11) називається першою формулою Муавра.
(1.11)
(1.11')
Приклад. Знайти за формулою Муавра (1 i)4 .
Розв’язання. Оскільки |
1 i 2 |
|
cos |
|
i sin |
|
, то |
||||||
|
|
|
|
||||||||||
(1 i)4 |
|
|
|
|
|
4 |
|
4 |
|
|
4 |
|
|
|
cos |
|
i sin |
|
|
4 cos i sin 4 . |
|||||||
2 |
|
||||||||||||
|
4 |
|
|||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
||
Якщо у формулі Муавра покласти |
r 1 |
, розкласти за формулою бінома |
|||||||||||
Ньютона ліву частину рівності
(cos isin )n cosn isin n
11
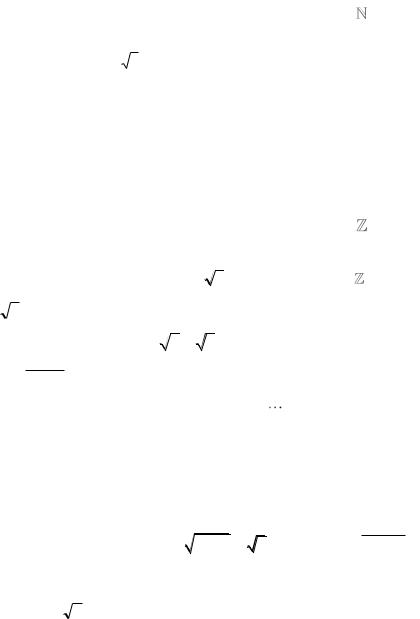
і прирівняти дійсні та уявні частини отриманого виразу, то матимемо формули для тригонометричних функцій кратних кутів.
Приклад. Знайти cos3 і sin3 .
Розв’язання. Запишемо
(cos isin )3 cos3 isin3
і розкладемо ліву частину рівності як куб суми:
(cos i Врахуємо, що i2 (cos
3 |
3 |
|
2 |
sin 3i |
2 |
2 |
|
||
sin ) |
cos |
3icos |
|
cos sin |
|
||||
1, i3 |
i |
|
|
|
|
|
|
|
|
|
3 |
3 |
|
2 |
|
|
2 |
|
|
isin ) cos |
3icos |
sin 3cos sin |
|||||||
i3 sin3
isin3 ,
.
підставимо праву частину у ліву частину формули Муавра
3 |
2 |
sin 3cos sin |
2 |
3 |
cos3 isin3 |
cos |
3i cos |
|
isin |
і прирівняємо дійсні та уявні члени у обох частинах рівності. Отримаємо
|
|
|
cos3 cos3 3cos sin2 , |
sin3 3cos2 sin sin3 . |
|
|||||||
1.3.5. Добування кореня з комплексного числа |
з комплексного чи- |
|||||||||||
Операція добування кореня степеня |
|
|
n |
|||||||||
|
|
|
|
|
|
|
|
n |
|
, n 1 |
|
|
сла z визначається як обернена до операції піднесення до степеня |
n : ком- |
|||||||||||
плексне число w |
n |
z називається коренем степеня n з комплексного числа |
||||||||||
|
||||||||||||
z , якщо |
w |
n |
z |
. Покладемо |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
z r (cos isin ), |
w (cos isin ) , |
|
||||
тоді з означення кореня випливає, що
n |
(cosn isin n ) r (cos |
|
isin )
.
Як відзначалося раніше, умова рівності двох комплексних чисел у тригонометричній та показниковій формах має вигляд
|
|
|
|
|
n |
r , |
n 2k |
(k |
) , |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
звідки маємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
n |
r , |
|
2k |
(k |
) , |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
де |
n |
r |
– додатне значення кореня з додатного числа |
r |
|||||||||||||
|
|||||||||||||||||
|
|
|
n |
z |
n |
r |
|
cos |
2k |
i sin |
2k |
||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
n |
|
n |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
. Отже,
|
, |
|
|
|
|
(1.12)
де k 0, n 1. Формула (1.12) називається другою формулою Муавра. Якщо
надаватимемо числу |
k |
значення 0,1, , n 1 , то отримаємо |
n |
різних значень |
кореня n -го степеня. Інші значення кореня матимуть аргументи, які відрізняються від отриманих раніше на доданки, що кратні до 2 , тому відповідні значення кореня будуть співпадати. Таким чином, існує рівно n різних значень кореня степеня n з комплексного числа z 0 . У показниковій формі запису формула (1.12) має вигляд
|
|
|
|
|
|
i |
2k |
|
|
|
|
n |
r e |
i |
|
n |
r e |
n |
, |
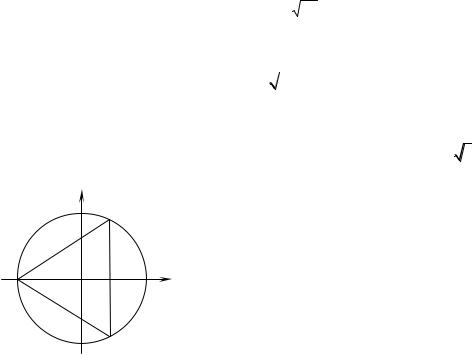
k 0, n 1 . |
(1.12') |
||
|
Точки на комплексній площині, що відповідають різним значенням кореня, розташовані у вершинах правильного n -кутника, вписаного до кола радіуса n r з центром у точці z 0 .
12
Приклад. Знайти всі значення |
3 |
1 |
та зобразити їх на комплексній |
|||||||||||||||||||||||
|
||||||||||||||||||||||||||
площині. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, то згідно (1.12): |
|||||||||
Розв’язання. Оскільки |
1 |
1 |
cos isin |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
cos i sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
w |
1 |
|
|
|
3 |
i , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
0 |
|
3 |
|
3 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
w1 cos i sin 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
||||||||||
w2 |
cos |
|
i sin |
|
|
|
cos |
|
|
i sin |
|
|
|
|
|
|
|
|
i. |
|||||||
3 |
3 |
|
3 |
2 |
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||
y |
|
|
|
|
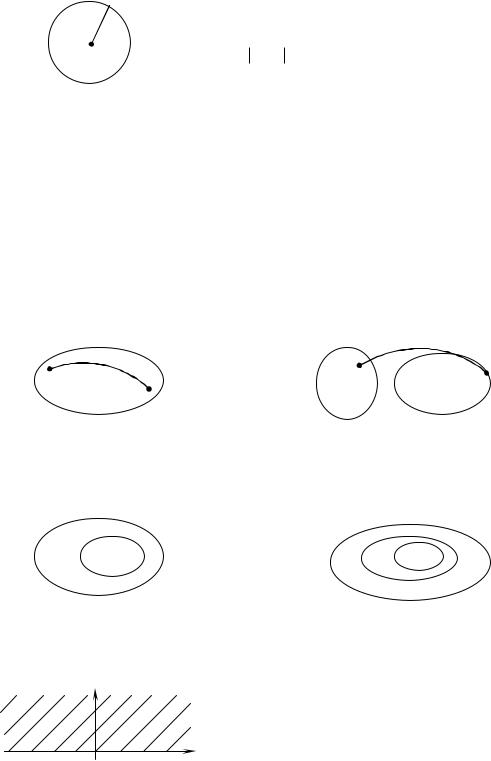
Отже, точки, що зображують ці числа, розта- |
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
w0 |
|
шовані у вершинах правильного трикутника, впи- |
||||||||||||||||||||||||
|
|
|
саного у коло радіуса |
R 1 |
з центром у точці z 0 . |
|||||||||||||||||||||
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13
2. Диференціальне числення функцій комплексної змінної
2.1. Області на комплексній площині
|
Множина точок z комплексної площини, що ле- |
||||
жать всередині кола радіуса |
|
з центром у точці z0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
z0 |
(для яких z z0 ), називається -околом точки z0 . |
|
|
||
Точка z називається внутрішньою точкою множини G , якщо існує |
|
- |
|||
|
|
|
|
|
|
окіл точки z , усі точки якого належать множині G . |
|
|
|
||
Множина G |
точок комплексної площини z |
називається областю, |
як- |
||
що разом із точкою цій множині належить і деякій окіл цієї точки (тобто кожна точка множини є її внутрішньою точкою).
Точка
z
називається зовнішньою точкою області G , якщо існує
-
окіл точки |
z , усі точки якого не належать області G . |
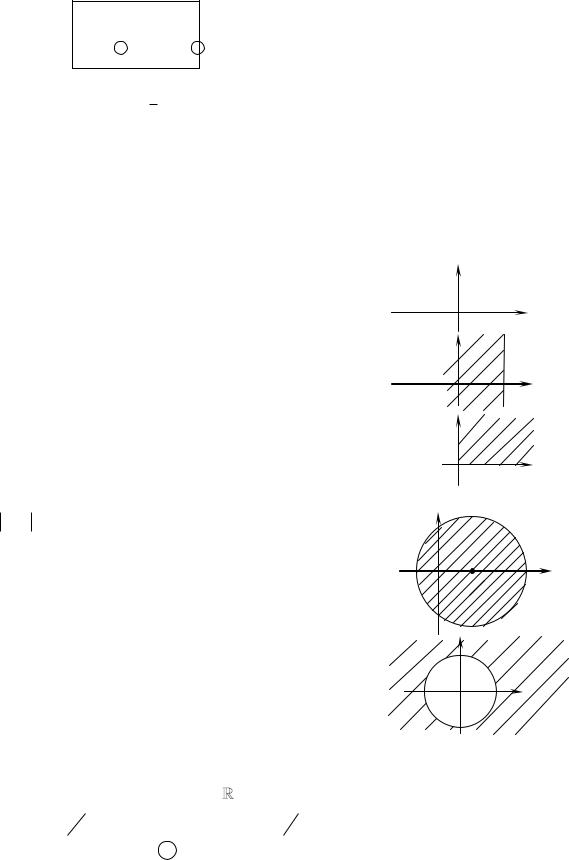
Область G називається зв’язною, якщо будь-які дві точки області можна з’єднати неперервною лінією, кожна точка якої належить цій же області. Зв’язна область становить одну цілу частину.
G |
G |
G |
G – зв’язна Зв’язна область G
G – не зв’язна називається однозв’язною, якщо будь-яку замкнену
криву, що лежить у цій області, можна стягнути у точку, що також належить цій області.
● |
● |
G |
G |
G – однозв’язна |
G – не однозв’язна |
Область G називається скінченною, якщо існує такий круг скінченного радіусу, всередині якого повністю знаходиться область G .
G |
|
G |
|
|
|
|
|
Верхня півплощина не є скінчен- |
Відкритий прямокутник є скінчен- |
||
ною областю |
ною областю |
||
Точка z називається межовою точкою області G , якщо у будь-якому її -околі містяться як точки, що належать області G , так і точки, що не належать області G . Сукупність усіх межових точок називається межею області G .
14
● M
G
Т. Т.
● M
M M
–межова точка.
–не є межовою точкою.
Область G |
разом зі своєю межею називається замкненою областю і по- |
значається символом G .
Надалі ми будемо розглядати області, для яких межа є одною або декількома кусково-гладкими кривими, які, у деяких випадках, можуть вироджуватися в окремі точки. Додатним напрямом обходу межі вважається такий, при якому область залишається ліворуч.
Приклад. Встановити множину точок комплексної площини, які задовольняють наступним умовам.
1) Im z c (c 0) |
|
y |
|
|
y c |
||
Це є сукупність точок, що лежать на прямій |
y c . |
||
|
2) |
Re z 5 |
|
|
|
Це є сукупність точок, що лежать на прямій |
x 5 |
|||
та ліворуч від неї. |
|
|||
3) |
0 arg z |
|
|
|
2 |
|
|||
|
|
|
|
|
Це |
є сукупність точок, що лежать на променях |
|||
0, |
|
та між ними. |
|
|
2 |
|
|||
|
|
|
|
|
4) |
z 2 3 |
|
|
|
Це є сукупність точок, що знаходяться всередині кола радіуса R 3 з центром у точці (2, 0) .
5)  z
z  5
5
Це є сукупність точок, що знаходяться на колі ра-
діуса |
R 5 |
з центром у точці (0, 0) та за його ме- |
жами. |
|
|
O
y
O y
O
y
–1 |
O |
2 |
|
y |
–5 |
O |
x
5 |
x |
|
x
5 |
x |
|
5 |
x |
|
2.2. Стереографічна проекція комплексної площини на сферу
У тривимірному просторі |
3 |
|||
|
|
|
|
|
радіуса R |
1 |
2 |
з центром у точці |
|
|
|
|
||
|
|
|
|
|
зкоординатами
0, 0, 12 . Площина
,, 0
задамо сферу |
S |
співпадає з ком-
плексною площиною |
z . Будемо вважати, що полюсами сфери є точки |
O( 0, 0, 0 ) і |
P( 0, 0,1 ) . Нехай точка |
M ( , , ) – довільна фіксована точка |
сфери, яка |
не співпадає з полюсом |
P (M S, M P) . Проведемо промінь |
PM до перетину з площиною z у точці z x i y .
15

P
O
(x)
z
( y)
Точка |
M |
називається стереографічною проекцією точки |
z |
на сферу |
S . |
Ця проекція встановлює взаємно однозначну відповідність між всіма точка-
ми комплексної площини |
z |
та всіма точками сфери |
S |
за виключенням точ- |
ки P . |
|
|
Доповнимо комплексну площину |
z |
ідеальним елементом, якому пос- |
тавимо у відповідність полюс P . Цей елемент назвемо нескінченно віддале- |
||
ною точкою і позначимо його символом |
z . Площина комплексних чисел |
|
z , доповнена ідеальним елементом z , називається розширеною площи- |
||
ною комплексних чисел. Стереографічна проекція встановлює взаємно однозначну відповідність між розширеною площиною комплексних чисел і сфе-
рою S . Сфера |
S називається сферою Рімана. |
|
|
|
|||||
Для числа |
z встановлюються наступні правила: |
|
|
||||||
1) |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) |
не визначені такі поняття, як Re z, Im z, Arg z, arg z |
; |
|
||||||
3) під околом точки z розуміють множину точок |
z R |
; |
|||||||
|
|||||||||
4) |
приймемо за означенням, що |
|
|
|
|||||
|
|
|
, z z , |
z ; |
|
|
|||
|
|
|
, z z , z , z 0; |
|
|
||||
|
|
|
|
, |
z |
0, z ; |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
z |
|
|
|
|
|
|
5) |
приймемо, що не визначені результати таких операцій, як |
||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
, 0 , / , 1 , . |
|
|
|||
2.3. Функції комплексної змінної
y |
|
|
z |
D |
● z |
O |
x |
v |
|
|
|
|
w |
G |
● |
w |
|
||
O |
|
u |
|
Нехай задані дві множини комплексних чисел: область |
D з елемента- |
ми |
z та область G з елементами w . Якщо кожному значенню |
z з області D |
за деяким законом ставиться у відповідність певне значення w з області G , то будемо казати, що в області D визначена функція комплексної змінної: w f (z) . Область D називається областю визначення функції, область G –
областю значень функції.
16

Функція |
w f (z) |
називається однозначною, якщо кожному значенню |
z D ставиться у відповідність тільки одне значення w G , у протилежному |
|
випадку функція називається багатозначною. Однозначна функція f (z) |
на- |
зивається однолистною функцією в області D , якщо у різних точках z |
цієї |
області вона приймає різні значення: |
|
z , z |
D : z |
z |
f (z ) |
|
1 |
2 |
1 |
2 |
1 |
f
(z |
) |
2 |
|
.
Геометрично функцію комплексної змінної будемо зображувати на
двох площинах комплексних чисел: z і |
w |
, де у площині |
z зображена |
||
множина D , а у площині |
w |
– множина |
G . Графік функції комплексної |
||
|
|
|
|
|
|
змінної не існує. Будемо говорити, що функція w f (z) відображує область D комплексної площини z на область G комплексної площини w . Точка
w називається образом точки |
z , а точка |
z |
називається прообразом точки w |
; функція |
w f (z) |
називається відображенням області |
D |
на область |
G . |
Якщо точка z пробігає |
D , то точка w пробігає G . Дослідити функцію ком- |
|||
плексної змінної – це означає вивчити закономірності відображення D на |
||||
G . |
|
|
|
|
Очевидно, що встановлюється і обернена відповідність – кожній точці |
||||
w G ставиться у відповідність одна або декілька точок z області D . Це |
||||
означає, що в області |
G |
задана (однозначна або многозначна) функція |
||
комплексної змінної |
w |
: |
z (w) . Вона називається оберненою до функції |
|
|
|
|
|
|
f (z) . Область G визначення функції (w) є областю значень функції f (z) ; |
||||
областю D значень функції (w) є область визначення функції |
f (z) . Якщо |
|||
функція (w) однозначна в області G , то між областями D і G |
встановлю- |
|||
ється взаємно однозначна відповідність.
Оскільки кожне комплексне число характеризується парою дійсних
чисел, то завдання комплексної |
функції w f (z) |
комплексної |
змінної |
|||||||||||||||||||||
z x i y |
еквівалентне |
до завдання |
двох |
|
дійсних |
|
функцій двох |
дійсних |
||||||||||||||||
змінних: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (z) u(x, y) iv(x, y) . |
|
|
|
|
|
|||||||||||||
Функції |
u( x, y ) Re f (z) |
та v( x, y ) Im f (z) |
називаються, відповідно, дійсною та |
|||||||||||||||||||||
уявною частинами функції |
|
w f (z) . |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||
Приклад. Знайти дійсну та уявну частини функції w z |
2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язання. Покладемо z x i y , тоді |
|
|
|
|
|
|
|
|
||||||||||||||||
|
z |
2 |
(x i y) |
2 |
x |
2 |
|
2ix y i |
2 |
y |
2 |
(x |
2 |
2 |
) |
2ix y , |
|
|
|
|||||
|
|
|
|
|
|
|
y |
|
|
|
||||||||||||||
звідки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(x, y) x |
2 |
|
2 |
, |
v(x, y) 2x y . |
|
|
|
|
|
||||||||||
|
|
|
|
|
y |
|
|
|
|
|
||||||||||||||
2.3.1. Алгебраїчні функції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1) лінійна функція w az b, |
|
a, b . |
|
|
|
|
|
|
|
|
|
|||||||||||||
Областю визначення і областю значень цієї функції є множина комплексних чисел D(w) , E(w) , функція є однозначною.
17

2) функція
w
1 z
.
Областю визначення і областю значень є множина комплексних чисел за ви-
ключенням нуля: D(w) |
\ 0 , |
E(w) |
\ 0 , функція однозначна. |
3) дробово-лінійна функція
w |
a z b |
, |
ad bc 0, |
|
c z d |
||||
|
|
|
c
0
.
Область визначення
D(w)
\
|
d |
|
c |
|
, область значень
E(w)
\
c |
|
|
|
a |
|
. Функція
однозначна, не вироджується в лінійну. |
n 1. |
|||||
4) степенева функція |
w z |
n |
, |
n |
, |
|
|
|
|
|
|
|
|
Областю визначення і областю значень цієї функції є множина комплекс-
них чисел D(w) |
, |
|
E(w) |
, функція однозначна. |
|
|
||||
5) функція w |
n |
z , n |
, n 1. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
Область визначення функції |
D(w) |
, |
область значень функції |
E(w) . |
||||||
Кожному значенню |
|
z 0 |
відповідають |
n різних значень |
w, тобто функція |
|||||
n -значна. |
|
|
|
|
|
|
|
|
|
|
2.3.2. Показникова функція
Показникова функція
w ez
визначається формулою
Область визначення
e |
|
def |
|
z |
e |
x |
|
D(w) |
|
||
e |
i y |
e |
x |
(cos y i sin y |
|
|
, область значень
) . E(w)
\
0
(2.1)
. Функція одно-
значна і періодична з
k 1 |
маємо e |
z 2 i |
e |
z |
|
|
|
періодом
e |
2 i |
1. |
|
2 i : |
z |
, k |
e |
z 2 ki |
|
ez
. Звідси при
Властивості показникової функції:
1) |
e |
z |
z |
|
e |
z |
|
e |
z |
|
; |
|
|
|
|
||||
1 |
|
2 |
1 |
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2) |
|
e |
|
e |
, |
|
Arg e |
|
y , |
e |
|
1. |
|||||||
|
|
|
|
z |
|
|
x |
|
|
|
|
|
|
|
z |
|
|
yi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Замінимо у формулі Ейлера y на y , а потім по черзі додамо і віднімемо отримані рівності:
|
e |
y i |
|
cos y i sin y |
|
e |
y i |
|
cos y i sin y |
|||||||
|
|
|
|
|
|
|||||||||||
e |
y i |
cos y i sin y |
e |
y i |
cos y i sin y |
|||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
e |
y i |
e |
y i |
2cos y |
|
e |
y i |
e |
y i |
2i sin y |
|||||
|
|
|
|
|
|
|
|
|||||||||
У результаті отримаємо вираз тригонометричних функцій через показникову:
|
e |
i y |
e |
i y |
|
|
|
||
cos y |
|
|
2 |
, |
|
|
|
|
|
e |
i y |
e |
|
|
|
|
sin y |
|
|
2i |
|
|
|
i y
.
Приклад. Обчислити значення функції eln
|
|
ln 2 |
i |
|
|
|
i |
|
|
|
|
|
|
Розв’язання. |
e |
|
e |
ln 2 |
e |
|
e |
ln 2 |
cos |
i sin |
|||
|
|
|
2 |
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
i |
2 . |
|
|
2(0 i) |
|
|
|
|
2i
.
2.3.3. Логарифмічна функція
Логарифмічна функція w Ln z визначається як функція, обернена до
показникової: число w називається логарифмом числа z , якщо ew z . Покладемо z r ei , w u iv , тоді eu eiv r ei , звідки eu r, v 2k . З
18

першої рівності знаходимо датного числа r . Тому w Ln z або, коротше,
uln
ln r
r – звичайний i ( 2k ) ln z
натуральний логарифм до-
i Arg z ,
Ln z ln z i Arg z |
(2.2) |
|
|
|
|
З цієї формули випливає, що логарифмічна функція комплексного аргуме-
нту є нескінченнозначною. При k 0 матимемо значення |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(2.2') |
|
|
|
|
|
|
|
|
ln z ln z i arg z |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
яке називається головним значенням логарифму. Якщо |
z |
– дійсне додатне |
||||||||||
число, то |
arg z 0 |
, і |
ln z ln |
|
z |
|
, тобто головне значення логарифма дійсного |
|||||
|
|
|||||||||||
|
|
|
|
|
||||||||
додатного числа збігається зі звичайним натуральним логарифмом цього числа.
|
Область визначення логарифмічної функції |
D(w) |
\ {0}, область зна- |
|||||||||
чень |
E(w) . |
|
|
|
|
|
|
|
||||
|
Властивості логарифмічної функції: |
|
|
|
||||||||
1) |
Ln (z1 z2 ) Ln z1 Ln z2 ; |
|
|
|
|
|||||||
2) |
Ln |
z |
Ln z1 |
Ln z2 ; |
|
|
|
|
||||
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
Ln z |
n |
n Ln z |
; |
|
|
|
|
||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||
4) |
Ln |
n |
z |
1 |
Ln z . |
|
|
|
|
|||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
Приклади. Знайти логарифми і головні значення логарифмів комплек- |
|||||||||||
сних чисел |
|
|
|
|
|
|
|
|
||||
1) |
z 2 ; 2) |
|
z i . |
|
|
|
|
|||||
|
Розв’язання. |
|
|
|
|
|
||||||
1) |
Знайдемо модуль числа: |
z 2 2 |
. Оскільки даному комплексному |
|||||||||
числу відповідає точка, що лежить на дійсній від’ємній півосі, то аргумент
. Тоді, згідно з формулами (2.2) і (2.2') відповідно, матимемо |
|
Ln( 2) ln 2 (2k 1) i, |
ln( 2) ln 2 i. |
2) Модуль числа дорівнює z i 1. |
Оскільки даному комплексному |
числу відповідає точка, що лежить на уявній додатній півосі, то аргумент
|
|
. Тоді, згідно (2.2) і (2.2') дістанемо |
|
|
|
||||
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
i |
|
|
|
Ln i |
2k |
|
|
i , |
ln i |
|
. |
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
2 |
|
2.3.4. Тригонометричні функції
Розглянемо означення та властивості наступних функцій комплексної змінної z .
1) Функція w sin z визначається рівністю
sin z |
ei z e i z |
; |
|
2i |
|||
|
|
тригонометричних
(2.3)
19

її область визначення |
D(w) |
, область значень |
на, непарна, періодична з періодом 2 .
2) Функція w cos z визначається рівністю
E(w)
, функція однознач-
|
|
|
e |
i z |
e |
i z |
|
|
|
|
|
||
|
|
cos z |
|
|
2 |
; |
|
|
|
|
|
|
|
її область визначення |
D(w) |
, область значень |
||||
на, парна, періодична з періодом 2 . |
|
|
|
|
||
3) Функція |
w tg z задана співвідношенням |
|||||
|
|
sin z |
|
e |
2i z |
|
|
tg z |
i |
|
|||
|
cos z |
e |
2i z |
|
||
|
|
|
||||
|
|
|
|
|||
E
1 1
(w)
;
(2.4)
, функція однознач-
(2.5)
її область визначення |
D(w) |
|
k, |
k |
|
, область |
|
\ |
|
|
|||||
|
|
|
2 |
|
|
|
|
функція однозначна, непарна, періодична з періодом . 4) Функція w ctg z визначена співвідношенням
значень
E(w)
,
|
|
|
cos z |
|
e |
2i z |
1 |
|
|
|
|
ctg z |
i |
2i z |
; |
(2.6) |
|||
|
|
sin z |
e |
1 |
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
її область визначення D(w) |
\ k, k |
, область значень E(w) |
, функція |
||||||
однозначна, непарна, періодична з періодом . |
|
|
|||||||
Для дійсних z |
ці означення тригонометричних функцій комплексної |
||||||||
змінної дають звичайні тригонометричні функції дійсного аргументу. При y 0, z x матимемо, наприклад,
|
e |
iz |
e |
|
|
|
|
sin z |
|
|
2i |
|
|
|
iz
|
(cos x i sin x) (cos x i sin x) |
|
2i sin x |
|
2i |
2i |
|||
|
|
sin
x
.
Для тригонометричних функції залишаються вірними усі співвідношення між функціями, наприклад
|
|
|
i z |
e |
i z 2 |
|
i z |
e |
i z 2 |
|
|
2i z |
2 |
e |
2i z |
2i z |
2 |
e |
2i z |
|
|
|||||||
sin2 |
z cos2 |
z |
e |
|
|
|
|
e |
|
|
|
|
e |
|
|
|
e |
|
|
|
4 |
1, |
||||||
|
|
2i |
|
|
|
2 |
|
|
|
4 |
|
|
|
4 |
|
|
4 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
тобто виконується основна тригонометрична тотожність
sin |
2 |
z cos |
2 |
z 1. |
|
|
Аналогічно можна довести інші тригонометричні відмінність функцій комплексного аргументу sin
співвідношення. Істотна z, cos z від функцій дійс-
ного аргументу полягає у тому, що вони не є обмеженими (див. область значень).
Приклади. Обчислити значення тригонометричних функцій
1) |
cos(i ln 2) |
; |
2) |
sin(i ln3) . |
Розв’язання.
1) Скориставшись формулою (2.4) і основною логарифмічною тотожністю, дістанемо
cos(i ln 2) |
e ln 2 |
eln 2 |
|
2 1 |
2 |
|
5 |
. |
|
2 |
2 |
4 |
|||||
|
|
|
|
|
||||
2) Скориставшись формулою (2.3) і основною логарифмічною тотожністю, матимемо
20
