
ifmion_kma_Mykhalin_Dujenkova(Mnozhyny)
.pdf
2.1. Властивостi дiйсних чисел |
|
61 |
|
jx x0j > a |
, x > x0 + a àáî x < x0 |
a , |
|
jx x0j > a |
, x 2 ( 1; x0 a) [ (x0 + a; +1). |
||
, x > x0 + a àáî x 6 x0 |
a |
, |
|
,x 2 ( 1; x0 a) [ [x0 + a; +1).
Çозначення модуля й арифметичного кореня дiста¹мо ще таку вла- ñòèâiñòü: px2 = jxj .
Ï ð è ê ë à ä 4. jx 3j < 1 , x 2 (2; 4); jx 3j > 1 , x 2
( 1; 2) [ (4; +1).
Проiлюстру¹мо доведення сформульованих властивостей на прикладi властивостей 3), 5), 6) i 7).
I ßêùî x > 0, òî jxj = x > x, à êîëè x < 0, òî jxj = x > 0 > x. Цим доведено властивiсть 3). J
I Нехай x y > 0. Тодi за властивiстю 3) jx yj = x y 6 jxj+ jyj. Аналогiчно, коли x y < 0, òî jx yj = x y 6 jxj + jyj. Îòæå,
jx yj 6 jxj + jyj:
Для доведення нерiвностi jjxj jyjj 6 jx yj розглянемо два випадки: 1) jxj jyj > 0 i 2) jxj jyj < 0.
У випадку 1) ма¹мо
jjxj jyjj = jxj jyj = j(x y) yj jyj 6 jx yj + jyj jyj = jx yj:
Аналогiчно дiста¹мо потрiбну нерiвнiсть у випадку 2). |
J |
||||||||||||||
I ßêùî xy > 0, òî àáî x > 0 |
i y > 0, àáî x < 0 i |
y < 0. Òîäi |
|||||||||||||
jxyj = x y = jxj jyj |
àáî jxyj = xy = ( x) ( y) = jxj jyj. |
|
|||||||||||||
ßêùî xy < 0, òî àáî |
x > 0 i y < 0, àáî x < 0 i y > 0. |
|
|||||||||||||
Òîäi jxyj = x ( y) = jxj jyj |
àáî jxyj = ( x) y = jxj jyj: |
||||||||||||||
У випадку, коли |
xy = 0, ìà¹ìî x = 0 àáî y = 0. |
|
|||||||||||||
Òîäi |
jxyj = 0 = jxj jyj. |
|
|
|
|
|
|
|
|
||||||
Öèì |
доведено, що |
jxyj = jxj jyj |
|
8x; y 2 |
R: |
|
|||||||||
|
x |
|
|
|
|||||||||||
Îñêiëüêè y |
|
= x; y 6= 0, то за доведеним вище ма¹мо: |
|||||||||||||
y |
|||||||||||||||
|
jxj = y y |
= jyj y |
) y |
= jjyjj; y 6= 0: |
|
||||||||||
|
|
|
|
|
x |
|
|
x |
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже, доведено властивiсть 6). J
Iз властивостей модуля випливають основнi властивостi вiдстанi :
1)(x; y) > 0 (íåâiä'¹ìíiñòü);
2)(x; y) = 0 , x = y (ðiâíiñòü íóëþ);
3)(x; y) = (y; x) (симетричнiсть);
4)(x; y) 6 (x; z) + (z; y) (нерiвнiсть трикутника).
I Нарештi, доведемо властивiсть 7). Нехай x > x0. Тодi x > x0 a i
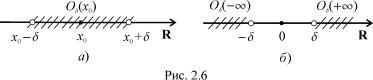
62 |
Роздiл 2. Множини дiйсних i комплексних чисел |
jx x0j = x x0 < a , x0 a < x < x0 + a , , x 2 (x0 a; x0 + a):
ßêùî x < x0, тобто x x0 < 0, òî x < x0 + a i
jx x0j = x0 x < a , x0 a < x < x0 + a , , x 2 (x0 a; x0 + a):
Аналогiчно можна довести iншi твердження властивостi 7). J
2.1.6. Поняття околу та проколеного околу точки
Зауважимо, що точка x0 ¹ центром iнтервалу (x0 ; x0 + ). Тому цей iнтервал називають околом àáî -околом точки x0 i позначають O (x0) (ðèñ. 2.6, à)). Îòæå,
O (x0) = (x0 ; x0 + ) = fx 2 R : jx x0j < g:
При цьому задане число > 0 називають ðàäióñîì -околу точки
x0.
ßêùî ç -околу точки x0 вилучити точку x0, то дiстанемо проколений окiл àáî проколений -окiл точки x0, який позначають O (x0).
O (x0) = O (x0) n fx0g = (x0 ; x0) [ (x0; x0 + ):
Зрозумiло, що проколений окiл можна задати нерiвнiстю
0 < jx x0j < ; àáî x0 < x < x0 + i x 6= x0:
Îêië àáî -окiл нескiнченно вiддалено¨ точки +1 ( 1) визнача¹ться рiвнiстю
O (+1) := ( ; +1) =: O(+1) (O ( 1)) = ( 1; ) =: O( 1)):
Проколений окiл нескiнченно вiддалено¨ точки збiга¹ться з вiдповiдним околом цi¹¨ точки.
Геометричну iлюстрацiю околiв нескiнченно вiддалених точок дано на рис. 2.6, б).
Ï ð è ê ë à ä 5. ßêùî = 1, òî O (2) = (2 1; 2 + 1) = (1; 3),
O (2) = (1; 2) [ (2; 3); O (+1) = (1; +1) = O (+1), a O ( 1) = ( 1; 1) = O ( 1).

2.1. Властивостi дiйсних чисел |
63 |
2.1.7. Iсторична довiдка
Перша теорiя дiйсних чисел була побудована, мабуть, ще древньогрецьким математиком Евдоксом Книдським (близько 408 355 р. до н.е.).
Сучасна теорiя дiйсних чисел веде початок вiд робiт нiмецького математика Гаусса (1777 1855), чеського математика Б. Больцано, французького математика О. Кошi (1789 1857) та завершена в трудах нiмецьких математикiв Р. Дедекiнда (1831 1916), К. Вей¹рштрасса (18151897) i Г. Кантора.
Позначення " sup " пiшло вiд латинського supremum найвищий, а " inf " вiд латинського infimum найнижчий.
2.1.8. Зв'язок iз шкiльним курсом математики
У шкiльному курсi математики основнi властивостi дiйсних чисел вивчають протягом майже всiх рокiв навчання. Однак досить часто вчителi не розумiють, що властивостi I-IY ¹ визначальними для множини дiйсних чисел. Найменшу увагу в шкiльному курсi математики придiлено властивостi неперервностi дiйсних чисел, без яко¨ не можна побудувати строго¨ теорi¨ математичного аналiзу.
2.1.9. Постановка проблем
Введене означення множини R дiйсних чисел не з'ясову¹ питання
про iснування множини R i, тим паче, не вказу¹ прикладу множини,
яку можна було б вважати множиною дiйсних чисел. Цю проблему пiзнiше буде розв'язано.
2.1.10. Контрольнi запитання та завдання
1. Перевiрити, чи правильними ¹ такi твердження:
1)властивостi суми задають правила, за якими завжди можна знайти суму двох дiйсних чисел;
2)äëÿ будь-яких чисел a; b i c iсну¹ ¨х сума, яку можна визначити
ÿê a + (b + c) àáî (a + b) + c;
3)iсну¹ число a, яке не ма¹ протилежного;
4)9 a 2 R : ( a) = a;
5)iсну¹ число a, яке не ма¹ оберненого;
6)8a 2 R 9! a 1 : a a 1 = 1;
7) (a b)c = ac bc 8a; b; c 2 R;
8)ÿêùî a 6 b i b 6 a, òî a = b;
9)ÿêùî a > b i c > d, òî ac > bd;
10)ÿêùî A R B R i A 6 B, òî 9 ! c : A 6 c 6 B;
11)ÿêùî a > 0, òî ( a) < 0;
12)кожна множина E R обмежена зверху;
13)8E R 9 max E òà min E;
14)8E R 9 sup E òà inf E;
64 |
Роздiл 2. Множини дiйсних i комплексних чисел |
15)кожний числовий промiжок ¹ обмеженою множиною в R;
16)ÿêùî [a; b] R, òî [a; b] обмежена множина;
2. Нехай A + B = fc = x + y : x 2 A; y 2 Bg. Довести, що sup(A + B) = sup A + sup B, a inf(A + B) = inf A + inf B.
2.2. Множина N натуральних чисел
Розглянемо одну з найважливiших пiдмножин множини дiйсних чисел, а саме множину натуральних чисел. Саме з не¨ почнемо процес побудови конкретно¨, а не абстрактно¨ множини дiйсних чисел, тоб-
то почнемо процес розв'язування проблеми, поставлено¨ у п. 2.1.9.
2.2.1. Поняття iндуктивно¨ множини
Iндуктивною множиною називають довiльну множину A R, яка задовольня¹ такi умови: 1) 1 2 A i 2) ÿêùî a 2 A, òî é (a + 1) 2 A.
П р и к л а д 1. Множини R, Z, [1; +1) i ( 1; +1) ¹ iндуктивними.
Множиною натуральних чисел називають множину N, яка ¹ перерiзом усiх iндуктивних множин. Натуральне число це елемент множини N.
Неважко помiтити, що перерiз будь-яко¨ сiм'¨ iндуктивних множин також ¹ iндуктивною множиною (пропону¹мо читачевi довести це самостiйно). Звiдси виплива¹ таке твердження.
Теорема 1 (п р о i н д у к т и в н i с т ь м н о ж и н и N). Множина N
натуральних чисел ¹ iндуктивною, тобто 1 2 N i з умови n 2 N виплива¹, що n + 1 2 N.
Зокрема, 1 + 1 =: 2 2 N, 2 + 1 =: 3 2 N, 3 + 1 =: 4 2 N, 4 + 1 =: 5 2
N, 5 + 1 =: 6 2 N, 6 + 1 =: 7 2 N, 7 + 1 =: 8 2 N, 8 + 1 =: 9 2 N. Öi
символи вiд 1 до 9, а також число 0 називають десятковими знаками. Нижче буде показано, що кожне натуральне (i, навiть, кожне дiйсне) число можна зобразити за допомогою десяткових знакiв. Напри-
êëàä, 9 + 1 =: 10, 10 + 1 =: 11 òîùî.
2.2.2. Принцип та метод математично¨ iндукцi¨
Оскiльки для будь-яко¨ iндуктивно¨ множини A ма¹мо включення N A, òî ç óìîâ A N i A iндуктивна множина виплива¹, що A = N. Тому ма¹ мiсце таке твердження.
Теорема 2 (п р о п р и н ц и п м а т е м а т и ч н о ¨ i н д у к ц i ¨). ßêùî
A N, 1 2 A та з умови a 2 A виплива¹ умова a + 1 2 A, то
A = N.
На практицi множину A, про яку йдеться в теоремi 2, пов'язують
з деяким твердженням Tn ðiâíiñòþ A = fn 2 N: твердження Tn ïðà-
вильне}, а тому принцип математично¨ iндукцi¨ часто формулюють так.
2.2. Множина N натуральних чисел |
65 |
||
Теорема 2 |
(ï ð î |
ï ð è í ö è ï ì à ò å ì à ò è ÷ í î ¨ i í ä ó ê ö i ¨). Íå- |
|
хай твердження |
Tn |
правильне для n = 1 i з припущення, що воно |
|
правильне для n = k, виплива¹ його правильнiсть для |
n = k + 1. Òîäi |
||
твердження Tn правильне для будь-якого натурального числа n. |
|||
З принципом математично¨ iндукцi¨ тiсно пов'язаний |
метод мате- |
||
матично¨ iндукцi¨ доведення певних тверджень. |
|
||
Суть цього методу розкрива¹ться такою евристичною схемою:
1)перевiрити правильнiсть твердження для n = 1;
2)припустити, що це твердження правильне для n = k;
3)довести правильнiсть твердження для n = k + 1;
4)згiдно з принципом математично¨ iндукцi¨, зробити висновок, що твердження праильне для всiх n 2 N.
2.2.3.Найпростiшi властивостi натуральних чи- сел
Вкажемо на деякi властивостi множини натуральних чисел, якi неважко довести методом математично¨ iндукцi¨.
Властивiсть 1 (п р о д о д а т н i с т ь н а т у р а л ь н и х ч и с е л). Будьяке натуральне число ¹ додатним, тобто n > 0 8n 2 N.
I У п. 2.1.3 (властивiсть 4) показано, що 1 > 0. Припустимо, що n > 0. Тодi за властивостями III 3 i I4 множини дiйсних чисел ма¹мо n + 1 > 0 + 1 = 1 > 0. Отже, за принципом математично¨ iндукцi¨ n > 0 8n 2 N. J
З означення множини N виплива¹, що 8n 2 N iсну¹ число n+1 2 N. При цьому число n + 1 називають наступником числа n. Виника¹ питання, що можна сказати про число n 1, яке природно назвати попередником числа n. Вiдповiдь на це питання да¹ наступна властивiсть.
Властивiсть 2 (п р о i с н у в а н н я п о п е р е д н и к а). ßêùî n 2 N i n 6= 1, òî n 1 2 N.
I Розглянемо множину E = fn 2 N : n = 1 àáî n 1 2 Ng. Òîäi E N; 1 2 E i з умови, що n 2 E, виплива¹, що й n + 1 2 E. Тому за принципом математично¨ iндукцi¨ E = N, тобто 8n 2 N ìà¹ìî àáî
n = 1, àáî n 1 2 N. J |
÷ è ñ ë î ): 1 = |
Властивiсть 3 (п р о н а й м е н ш е н а т у р а л ь н е |
|
min N. |
1 2 E i, ÿêùî |
I Для множини E = fn 2 N : n > 1g ìà¹ìî |
n 2 E, тобто n > 1, то враховуючи, що 1 > 0 (властивiсть 4, п. 2.1.3) ма¹мо n + 1 > 1 + 0 = 1 > 0, тобто n + 1 2 E. Згiдно з принципом математично¨ iндукцi¨, E = N, тобто n > 1 8n 2 N , 1 = min E. J
Отже, множина N ма¹ найменший елемент. Виника¹ питання, чи iсну¹ min E, êîëè ? 6= E N.
66 Роздiл 2. Множини дiйсних i комплексних чисел
I Оскiльки множина E обмежена знизу, наприклад одиницею, то за теоремою Вей¹рштрасса iсну¹ inf E = .
Якщо припустити, що 62E, то за наслiдком 3 (критерiй iнфiмуму) з п. 2.1.4 iсну¹ таке число n0 2 E, ùî < n0 < + 1.
Îñêiëüêè n0 1 < , òî n > n0 8n 2 E, а це суперечить тому, що
= inf E.
Îòæå, 2 E, i òîìó = min E. J Цим доведено таку властивiсть.
Властивiсть 4 (п р о н а й м е н ш и й е л е м е н т п i д м н о ж и н и м н о ж и н и N). ßêùî ? 6= E N, òî iñíó¹ min E.
Доведемо тепер таку властивiсть.
Властивiсть 5 (п р о д и с к р е т н i с т ь м н о ж и н и N). ßêùî n 2
N, òî (n 1; n) \ N = ?.
I Нехай E = fn 2 N : (n 1; n) \ N = ?g. Òîäi 1 2 N, îñêiëüêè (0; 1) \ N = ?, а останн¹ виплива¹ з того, що 1 = min N.
Припустимо, що n 2 E, тобто (n 1; n) \ N = ?. Тодi, якщо вважати, що n+1 62E, тобто (n; n+1)\N 6= ?, òî m 2 (n; n+1)\N , n < m < n + 1 , n 1 < m 1 < n i m 1 2 N.
Îòæå, m 1 2 (n 1; n) \ N, що неможливо за припущенням. Таким чином, 1 2 E i (n 2 E ) n + 1 2 E), а тому за принципом
математично¨ iндукцi¨ ма¹мо E = N, тобто
(n 1; n) \ N = ? 8n 2 N. J
Властивостi 1 5 iлюструють застосування методу математично¨ iндукцi¨. Пропону¹мо читачевi застосувати цей метод для доведення наступно¨ властивостi.
Властивiсть 6 (п р о а р и ф м е т и ч н i о п е р а ц i ¨ н а д н а т ур а л ь н и ч и с л а м и). Якщо m i n натуральнi числа, то ¨х сума i добуток
¹ натуральними числами, а якщо m n > 0, то й рiзниця m n ¹ натуральним числом.
Нагада¹мо, що множину fk 2 N : 1 6 k 6 ng позначають 1; n. Аналогiчно розумiтимемо позначення 0; n = fk 2 N0 : 0 6 k 6 ng, äå N0 множина цiлих невiд'¹мних чисел.
Властивiсть 7 (i н ш а ф о р м а п р и н ц и п у м а т е м а т и чн о ¨ i н д у к ц
Якщо E N i з того, що 1; n 1 E виплива¹, що n 2 E 8n 2 N, то E = N.
I Покажемо, що N E. Припустимо супротивне. Нехай iсну¹ n0 2 N, òàêå, ùo n0 62E. Тодi множина F = fn 2 N : n 62Eg непорожня i
ма¹ найменший елемент |
min F = n1. Зрозумiло, що n1 6= 1, îñêiëüêè |
|||
1; 1 1 |
= |
1; 0 |
= ? E, |
тобто 1 2 E. |
Îòæå, ÿêùî 1; n1 1 E, òî n1 2 E, проте n1 2 F , à òîìó n1 62E. Одержане протирiччя й доводить наше твердження. J
2.2. Множина N натуральних чисел |
67 |
2.2.4. Принцип Архiмеда
Множина N обмежена знизу. А чи обмежена вона зверху?
I Припустимо, що це так. Тодi iсну¹ sup N = < +1, à òîìó n 6 8n 2 N.
З iншого боку, за критерi¹м супремуму iсну¹ таке m 2 N, ùî m >1, çâiäêè m + 1 2 N i m + 1 > , що суперечить нерiвностi n 6
8n 2 N J
Отже, доведено таку властивiсть.
Властивiсть 8 (п р и н ц и п А р х i м е д а). Множина N необмежена зверху, тобто для будь-якого числа a 2 R знайдеться таке n 2 N, що n > a.
2.2.5. Нерiвнiсть Бернуллi
Для доведення наступно¨ властивостi натуральних чисел введемо такi позначення:
Q |
Q |
Q |
1 |
n+1 |
n |
k=1 ak := a1; |
k=1 ak := k=1 ak an+1; |
|
P |
P |
kP |
1 |
n+1 |
n |
ak := a1; |
ak := |
ak + an+1; |
k=1 |
k=1 |
=1 |
äå a1; a2; : : : ; an заданi дiйснi числа, а n довiльне фiксоване на-
туральне число. |
|
n |
|
|
|
|
|
|
nn 2 N |
|
k 2 |
|||
За принципом |
|
|
|
|
|
|
|
|
||||||
|
|
|
математично¨ iндукцi¨ для будь-якого |
|
i |
|
||||||||
|
|
|
Q |
ak добуток чисел ak òà |
kP |
|
|
|||||||
чисел ak. |
|
|
|
|||||||||||
1; n визначено вирази: |
|
|
|
ak ñóìà |
||||||||||
|
|
|
|
k=1 |
|
|
|
|
|
|
=1 |
|
|
|
вають |
|
|
a ç |
|
|
|
|
|
n |
|
|
|
||
|
|
|
|
Q |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
Зокрема, якщо всi |
ak = a, òî |
|
ak =: an |
, i останнiй вираз нази- |
|||||||||
|
|
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
степенем числа |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
натуральним показником . |
|
|
|
|||||||
|
|
|
|
|
|
|||||||||
Покладемо також, що |
|
a0 := 1 |
степiнь числа |
a з показником |
||||||||||
0. |
Властивiсть 9 (н е р i в н i с т ь |
Á å ð í ó ë ë i). ßêùî |
a > 1, òî |
|||||||||||
|
||||||||||||||
(1 + a)n > 1 + na |
8n 2 N. |
|
|
|
|
|
|
|
|
|
||||
I Для n = 1 нерiвнiсть Бернуллi ста¹ очевидною рiвнiстю. Припустимо, що для n = k нерiвнiсть Бернуллi викону¹ться, тобто
(1 + a)k > 1 + ka:
Тодi для n = k+1 за означенням степеня i за властивостями дiйсних чисел (яких?) дiста¹мо:
(1 + a)k+1 = (1 + a)k(1 + a) > (1 + ka)(1 + a) =
=1 + ka + (1 + ka)a = 1 + ka + a + ka2 =
=1 + (k + 1)a + ka2 > 1 + (k + 1)a:

68 |
Роздiл 2. Множини дiйсних i комплексних чисел |
Отже, згiдно з принципом математично¨ iндукцi¨, нерiвнiсть Бернуллi правильна. J
Властивiсть 10 (п р о з р о с т а н н я т а о б м е ж е н i с т ь an). ßêùî
a > 1, òî an+1 > an |
8nn 2 N i для будь-якого c 2 R iсну¹ натуральне |
|||||||||||||
число n0 òàêå, ùî |
|
a > c äëÿ âñiõ n > n0. |
|
|
|
|
|
|
||||||
При цьому кажуть, що |
a |
n пряму¹ до |
+1 |
, êîëè |
n |
пряму¹ до |
1, |
|||||||
|
nlim a |
n |
|
|
n |
|
|
|
n |
|
||||
i записують |
|
= +1 àáî a |
|
! +1; n ! 1, àáî a |
|
+1; n |
||||||||
. |
!1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I Îñêiëüêè a > 1 i an > 0 (чому?), то за властивiстю III 4 дiйсних чисел ма¹мо a an > 1 an , an+1 > an.
Нехай число c 2 R довiльне фiксоване. Оскiльки a = 1+(a 1) = 1 + b, äå b = a 1 > 0, то за нерiвнiстю Бернуллi
an = (1 + b)n > 1 + bn; 1 + bn > c , n > c b 1 :
За принципом Архiмеда для числа |
|
c 1 |
|
|
|
|
|
|
n0 |
|
2 |
N, |
|||||||||||
|
|
|
c 1 |
|
|
|
|
|
|
|
b знайдеться таке |
|
|
|
|
||||||||
ùî n0 |
> |
|
|
an |
> |
an0 > c |
8 |
n |
> |
n0. |
J |
|
|
|
|
|
|
||||||
|
|
|
b . Тодi за доведеним |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
З властивостi 10 дiста¹мо таке твердження. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Íàñëiäîê (ï ð î ñ ï à ä à í í ÿ i ï ð ÿ ì ó â à í í ÿ ä î í ó ë ÿ an). ßêùî |
|||||||||||||||||||||||
0 < a < 1, òî 0 < an+1 < an |
|
8 |
n |
2 |
N, i |
|
|
" > 0 |
9 |
n0 |
|
2 |
N: |
||||||||||
|
n |
< " 8n > n0 |
|
|
|
|
|
|
8n |
|
|
|
|
|
|||||||||
0 < a |
|
. При цьому |
|
n |
|
|
|
|
|
a |
пряму¹ до нуля, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
||||||||||
|
|
|
|
|
|
|
кажуть, що |
|
|
|
|
|
|
|
|
|
|
||||||
коли n пряму¹ до 1 i записують a |
|
|
! 0; n ! 1, àáî |
nlim a |
|
|
= 0, |
||||||||||||||||
àáî an 0; n 1. |
|
|
|
|
|
|
|
|
|
|
|
|
!1 |
|
|
|
|
|
|||||
2.2.6. Десяткове зображення натуральних чисел
Тепер вже можна довести, що кожне натуральне число можна зобразити за допомогою десяткових знакiв.
I Зафiксу¹мо довiльне число c 2 N i введемо в розгляд множину E = fn 2 N : 10n > cg. За властивiстю 10 E 6= ?, а за властивiстю 4 iсну¹ min E = n0 ) 10n0 1 6 c < 10n0 .
Нехай m = n0 1. Òîäi m 2 N0 i 10m 6 c < 10 10m. Îñêiëüêè
10m < 2 10m < 3 10m < < 9 10m < 10 10m;
то iсну¹ ¹дине число k 2 1; 9 òàêå, ùî k 10m 6 c < (k + 1) 10m. Позначимо m = k. Òîäi
0 6 c m 10m < 10m = 10 10m 1:
ßêùî c m 10m < 10m 1, то вважатимемо, що m 1 = 0. В iншому разi знайдемо ¹дине можливе k 2 1; 9 òàêå, ùî
k 10m 1 6 c m 10m < (k + 1)10m 1;

2.2. Множина N натуральних чисел |
69 |
i позначимо m 1 = k. Òîäi
0 6 c m 10m m 1 10m 1 < 10m 1 = 10 10m 2:
Через скiнченну кiлькiсть крокiв аналогiчно дiстанемо
|
c |
k |
|
10 = 0, |
|
P |
0 = 0 |
|
||
|
|
|
|
|
|
|
m |
|
|
|
|
|
m |
|
|
0 6 c k=1 k 10k < 10: |
|
|
|||
знайдемо ¹динеPможливе 0 2 1; 9 таке, що |
|
|
||||||||
ßêùî |
|
k=1 |
|
|
k |
то вважатимемо |
|
. В iншому разi |
||
|
|
|
kP |
|
|
|
P |
|
|
|
|
|
|
m |
|
|
|
m |
|
|
|
|
|
c |
=1 k 10k = 0 , c = k=0 k 10k; |
|||||||
äå k 2 0; 9 8k 2 0; m; m 2 N0; m 6= 0.
Числа k називають десятковими цифрами, àáî десятковими розря-
дами числа c. При цьому 0 розряд одиниць, 1 розряд десяткiв,2 розряд сотень, 3 розряд тисяч, ... , n розряд 10n. Зобра-
|
|
|
|
mkP |
|
|
|
|
|
|
|
m |
|
ження числа c у виглядi |
c = |
=0 k 10k |
називають його десятковим |
|||
|
. Íà |
|
|
|
|
|
|
|
|
P |
|
||
зображенням, а сам вираз |
k=0 k 10k називають десятковим нату- |
|||||
ральним числом |
|
практицi його найчастiше записують у виглядi |
||||
c = m m 1 : : : 1 0. J
Отже, доведено таке твердження.
Властивiсть 11 (п р о д е с я т к о в е з о б р а ж е н н я н а т ур а л ь н о г о
÷ è ñ ë à). |
Для довiльного натурального числа |
c iснують ¹дине чи- |
||||||||
ñëî |
m 2 |
N0 |
i ¹äèíi |
|
|
|
|
, òàêi, ùî |
m 6= 0 i c = |
|
m |
|
k 2 0; 9; k 2 0; m |
|
|||||||
kP |
|
|
|
|
|
|
|
|
|
|
=0 k 10k =: m m 1 : : : 1 0. |
|
|
||||||||
|
Ï ð è ê ë à ä |
2. Десяткове зображення числа 9 740 352 ма¹ |
||||||||
вигляд: 9 740 352 = 9 106 + 7 105 + 4 104 + 0 103 + 3 102 + 5 10 + 2. З властивостi 11 виплива¹, що можна ототожнювати кожне нату-
ральне число з його десятковим зображенням. При цьому два нату- |
|||||||
|
k P k |
8 2 |
|
P |
|
|
|
|
m |
|
|
n |
|
|
|
ральнi числа |
c = k=0 k 10k |
i b = k=0 k 10k |
ðiâíi òîäi é òiëüêè òîäi, |
||||
êîëè m = n i |
= |
k |
|
|
|
|
|
0; m. |
c > b , m > n àáî |
||||||
Враховуючи властивiсть 10, дiста¹мо, що |
|||||||
m = n i m > m, àáî |
m = n i iсну¹ таке число k0 2 |
1; m |
: k = k, |
||||
êîëè k0 6 k 6 m i k0 1 > k0 1. |
|
|
|
||||
П р и к л а д 3. Натуральне число 1 250 110 = 6 5 4 3 2 1 0 >6 5 4 3 2 1 0 = 1 249 999, оскiльки 6 = 6, 5 = 5, a 4 > 4.
Отже, щоб порiвняти два десятковi натуральнi числа, послiдовно порiвнюють ¨хнi вiдповiднi розряди, починаючи з найстаршого, i роблять висновок за першою виявленою парою нерiвних розрядiв.
70 |
Роздiл 2. Множини дiйсних i комплексних чисел |
Тепер можна ввести операцi¨ додавання, множення та вiдношення "менше"для натуральних чисел так, як це зроблено у шкiльному курсi математики, i перевiрити, чи виконуються властивостi дiйсних чисел
I IV для множини N (пропону¹мо читачевi зробити це самостiйно).
2.2.7. Iсторична довiдка
Позначення N для множини натуральних чисел походить вiд ла-
тинського Natura природа.
Прообрази сучасних десяткових знакiв (цифр) та зображення у десятковiй системi числення з'явилося в Iндi¨ у V сторiччi до н.е. Араби занесли ¨х в вропу, де цi числа знайшли широке застосування.
Древньогрецькi математики вiдкрили властивостi нескiнченностi та необмеженостi множини натуральних чисел, що видно з робiт Евклiда (365 300 р.р. до н.е.) та Архiмеда (287 212 р.р. до н.е.).
Iдея зображення чисел на прямiй належить французькому математику Р. Декарту (1596 1650).
Питання про означення натурального числа виникло лише в ХIХ сторiччi. Першим його ввiв на основi поняття множини Г. Кантор.
Аксiоми натуральних чисел першими сформулювали нiмецький математик Р. Дедекiнд та iталiйський математик Д. Пеано.
Натуральнi числа служать основою для побудови iнших чисел. Нiмецький математик Л. Кронекер (1823 1891) висловився з цього приводу так: "Бог створив натуральнi числа, а все iнше справа рук людських".
Метод математично¨ iндукцi¨ по сутi першим сформулював французький математик Б. Паскаль (1623 1662). Нерiвнiсть Бернуллi названа на честь швейцарського математика Я. Бернуллi (1654 1705).
2.2.8. Зв'язок iз шкiльним курсом математики
У шкiльному курсi математики значну увагу придiляють вивченню тих властивостей натуральних чисел, якi необхiднi в повсякденному життi, зокрема, арифметичним операцiям над натуральними числами. Меншу увагу звертають на означення натуральних чисел, принцип математично¨ iндукцi¨, принцип Архiмеда, нерiвнiсть Бернуллi тощо. Однак вчителю математики вкрай необхiдно знати цi речi, щоб усвiдомлено викладати матерiал, який вивчають навiть у молодших класах.
Наприклад, вчитель повинен розумiти, що без принципу математично¨ iндукцi¨ не можна визначити степiнь з довiльним натуральним показником.
2.2.9. Постановка проблем
Уже вiдомо, що пiд натуральними числами слiд розумiти ¨хнi десятковi зображення. Виника¹ питання, чи можна для iнших чисел також ввести ¨хнi десятковi зображення.
