ifmion_kma_Mykhalin_Dujenkova(Mnozhyny)

òà частка f=' функцiй f i ' визначаються вiдповiдно рiвностями

(f + ')(x) := f(x) + '(x); (f ')(x) := f(x) '(x); (f ')(x) := f(x) '(x); (f=')(x) := f(x)='(x):

При цьому областю визначення перших трьох функцiй вважають перерiз D(f) \ D('), а у випадку частки D(f=') = D(f) \ D(') n fx :

'(x) = 0g.

За допомогою арифметичних операцiй, користуючись лише двома числовими функцiями сталою та тотожною, можна означити цiлi класи нових функцiй:

степеневi з цiлим показником : f(x) = xn, äå n 2 Z фiксоване;

лiнiйнi функцi¨: f(x) = ax + b, äå a 6= 0 i b 2 R (àáî C)

фiксованi числа;

квадратичнi функцi¨: f(x) = a x2 + b x + c, äå a 6= 0; b i c 2 R

(àáî C) фiксованi числа;

многочлени степеня n 2 N, àáî цiлi рацiональнi функцi¨: pn(x) = a0 + a1x + + anxn; äå ak 2 R 8k 2 0; n i an 6= 0;

рацiональнi функцi¨: R(x) = Pm(x) , äå Pm i Qn деякi много-

члени тощо.

Qn(x)

Кожну з названих функцiй можна розглядати i як функцiю комплексно¨ змiнно¨. Тодi замiсть x здебiльшого пишуть z.

П р и к л а д 17. Функцi¨ f(x) = 2x + 1 òà f(x) = x2 5x + 6

вiдповiдно лiнiйна та квадратична функцi¨ дiйсно¨ змiнно¨, а f(z) = 2z + 1 òà f(z) = z2 5z + 6 аналогiчнi функцi¨ комплексно¨ змiнно¨.

1.2.11. Iсторична довiдка

Уже в роботах французьких математикiв П. Ферма (1601 1655), Р. Декарта й англiйських математикiв I. Барроу (1630 1677) та I. Ньютона (1643 1727) фактично використову¹ться поняття функцiонально¨ залежностi.

Òåðìií "функцiя\ першим увiв у 1692 р. нiмецький математик Г. Лейбнiц (1646 1716), а перше означення функцi¨ ( "функцiя це вели-

чина, складена iз змiнно¨ та стало¨ \) зустрiча¹ться в 1718 р. у швейцарського математика I. Бернуллi (1667 1748). Йому та Л. Ейлеру належить позначення y = f(x).

Близьке до сучасного поняття функцi¨ зустрiча¹ться в роботах французького математика С. Лакруа (1765 1843), нiмецького математика

Ï.Дiрiхле (1805 1859) та росiйського М. Лобачевського (1792 1856). Упродовж свого розвитку поняття функцi¨ неодноразово узагаль-

нювалося та уточнювалося, що мало вiдповiдний вiдбиток на розглядi цього поняття у навчальних математичних курсах. Так, за останн¹ пiвстолiття в ролi функцi¨ в рiзних курсах математики виступали: змiнна величина, залежнiсть, правило, закон, вiдношення та вiдповiднiсть.

1.2.12. Зв'язок iз шкiльним курсом математики

У шкiльному курсi математики, можливо, й не слiд вводити поняття вiдповiдностi мiж множинами та залежностi мiж змiнними, а вважати його основним, розкриваючи суть цього поняття за допомогою багатьох конкретних, яскравих прикладiв.

Взагалi, поняття функцi¨ в шкiльному курсi математики можна ввести без використання поняття множини, проте вчитель повинен розумiти, що при цьому фактично один не визначений термiн "множина"замiнюють iншим або кiлькома iншими термiнами, якi можуть бути менш зрозумiлими, нiж термiн "множина".

Так, наприклад, досить поширеним ¹ таке означення: "функцi¹ю називають таку залежнiсть мiж змiнними величинами, при якiй кожному значенню однi¹¨ величини вiдповiда¹ одне значення iншо¨ вели- чини". Однак при цьому нiчого не кажуть, що таке "величина", "зна- чення величини"та "залежнiсть мiж величинами".

Квалiфiкований вчитель математики повинен бачити такi моменти й давати, при нагодi, вiдповiднi роз'яснення.

Запропонований вище спосiб введення поняття функцi¨ (вiдображення) по сво¨й сутi ¹ досить простим, оскiльки кожний крок можна iлюструвати простими прикладами. При цьому використову¹ться мiнiмальна кiлькiсть неозначуваних понять.

1.2.13. Постановка проблем

Основною проблемою, що виника¹ пiсля введення загального поняття функцi¨, ¹ введення означень конкретних функцiй, якi знаходять широке застосування на практицi. До таких функцiй вiдносяться, зокрема, так званi основнi елементарнi функцi¨, якi вивчають i в шкiльному курсi математики.

1.2.14. Контрольнi запитання та завдання

1. Перевiрити, чи правильними ¹ такi твердження:

1)кожна пара елементiв даних множин ¹ деякою множиною;

2)якщо двi пари складаються з однакових елементiв, то вони рiвнi;

3)твердження, обернене до 2), ¹ правильним;

10) вiдповiднiсть мiж множинами A i B iñíó¹ òà ¹äèíà 8A; B;

1) для будь-яко¨ мiри викону¹ться рiвнiсть

(A [ B) = (A) + (B) (A \ B);

2)ÿêùî A B, òî (B n A) = (B) (A);

3)ÿêùî A B, òî (A) 6 (B);

4)(?) = 0, êîëè 9A 2 D( ) : (A) < +1.

1.3. Найпростiшi властивостi та класифiкацiя числових функцiй.

Розглядаються найпростiшi властивостi числових функцiй: обмеженiсть, монотоннiсть (для функцi¨ дiйсно¨ змiнно¨), парнiсть, перiодичнiсть; вводиться поняття основних елементарних та елементарних функцiй.

1.3.1. Обмеженi функцi¨

Числову функцiю f називають:

обмеженою на множинi A D(f), ÿêùî 9 M > 0 : jf(x)j 6 M 8x 2 A;

необмеженою на множинi A D(f), якщо вона не ¹ обмеженою на цiй множинi, тобто

8M > 0 9x 2 A : jf(x)j > M;

обмеженою зверху (знизу) на множинi A D(f), ÿêùî

1.3..Найпростiшi властивостi та класифiкацiя числових функцiй. 25

9 M 2 R (m 2 R) : f(x) 6 M (f(x) > m) 8x 2 A;

необмеженою зверху (знизу) на множинi A D(f), ÿêùî

8M 2 R (m 2 R) 9x 2 A: f(x) > M (f(x) < m).

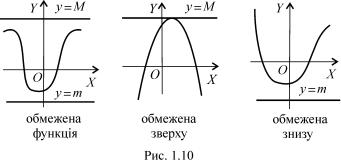
Розташування вiдносно прямих y = m i y = M ãðàôiêiâ ôóí-

êöié f, обмежених, обмежених зверху та обмежених знизу на множинi iлюстру¹ться на рис. 1.10.

ßêùî A = D(f), то в наведених означеннях слова "на множинi

AD(f)"можна опустити.

Ïð è ê ë à ä 1. 1) ßêùî D(f) = D(g) = D(') = R, то функцi¨: f(x) = sin x обмежена, g(x) = 1 x2 обмежена зверху i необмежена знизу, '(x) = x4 обмежена знизу i необмеженою зверху.

2) Функцii¨ f(x) = tg x, '(x) = x3 òà g(x) = loga x необмеженi (i зверху, i знизу).

Для обмежених на множинi функцiй часто вживають позначення f(x) = O(1); x 2 A (читають: еф вiд iкс дорiвню¹ о-велике вiд оди-

ницi). Замiсть слiв "функцiя f обмежена на множинi A зверху (знизу)"вживають позначення f(x) = OR(1) (f(x) = OL(1)); x 2 A, а функцiю f при цьому називають обмеженою на множинi A D(f)

справа (çëiâà).

Неважко помiтити, що коли f(x) 2 R 8x 2 A, то функцiя f îáìå-

жена на множинi A тодi й тiльки тодi, коли вона обмежена на A i

зверху, i знизу.

1.3.2. Монотоннi функцi¨

спадною, якщо з нерiвностi x1 < x2 виплива¹ нерiвнiсть f(x1) > f(x2) 8x1; x2 2 A;

монотонною, якщо вона ¹ неспадною або незростаючою на множинi A;

строго монотонною, якщо вона ¹ зростаючою або спадною на A.

ßêùî A = D(f), то в наведених означеннях слова "на множинi A D(f)\ можна опустити.

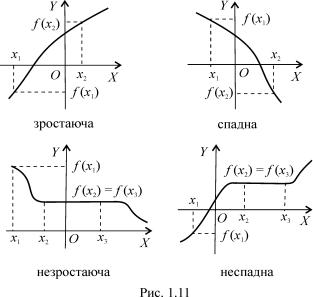
Вигляд графiка монотонно¨ функцi¨ залежно вiд характеру монотонностi зображено на рис. 1.11.

П р и к л а д 2. Функцi¨ f(x) = sign x (äèâ. ðèñ. 1.8), f(x) = x3, f(x) = sign x, f(x) = x3 ¹ вiдповiдно неспадною, зростаючою, незростаючою, спадною.

Для зростаючих (спадних) функцiй на множинi A вживають позначення f(x) " íà A (f(x) # íà A), а для неспадних (незростаючих)позначення f(x) % íà A (f(x) & íà A).

Зауважимо, що спадна функцiя ¹ незростаючою, а зростаюча неспадною.

Промiжком монотонностi функцi¨ f називають такий промiжок ha; bi, на якому f монотонна, а на ширшому промiжку hc; d i ha; bi

вже не ¹ монотонною. Вiдповiдно до характеру монотонностi дiста¹мо

промiжки зростання, спадання, незростання та неспадання . промiжком спадання

Усi iншi функцi¨ на множинi A називають нi парними, нi непарними.

1.3..Найпростiшi властивостi та класифiкацiя числових функцiй. 27

ßêùî A = D(f), то в наведених означеннях слова "на множинi A D(f)"можна опустити.

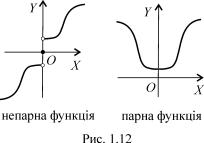
Графiк парно¨ функцi¨ симетричний вiдносно осi OY , а графiк непарно¨ вiдносно початку координат (рис. 1.12).

Ï ð è ê ë à ä 4. ßêùî

D(f) = D(g) = D(') = R, то функцi¨ а) f(x) = x2, á) g(x) = x3, â) '(x) = 1 + x ¹

вiдповiдно: а) парною, б) непарною, в) нi парною, нi непарною.

Функцiя y = x2; x 2 [0; +1)

також ¹ нi парною, нi непарною, оскiльки область ¨¨ визначення не ¹ симетричною

вiдносно точки 0.

Якщо множина D(f) симетрична вiдносно точки x = 0, то iсну¹ ¹дина пара функцiй ' i таких, що ' парна, a непарна на

D(f) i f(x) = '(x) + (x) 8x 2 D(f).

1.3.4. Перiодичнi функцi¨

Функцiю y = f(x), називають перiодичною на множинi A D(f), якщо iсну¹ число T 6= 0 òàêå, ùî x + T 2 A i f(x + T ) = f(x) 8x 2 A. При цьому число T називають перiодом функцi¨ f на множинi A.

ßêùî A = D(f), то в наведених означеннях слова "на множинi A D(f)"можна опустити.

Характер графiка перiодично¨ функцi¨ можна уявити на прикладi тригонометричних функцiй, якi вивчаються у шкiльному курсi математики. Неважко помiтити, що для побудови такого графiка доста-

тньо це зробити для якогось промiжку ha; bi D(f), довжина якого b a = T , де T перiод функцi¨ f.

I Справдi, якщо припустити, що mT перiод функцi¨ f, òî f(x+ (m + 1)T ) = f((x + mT ) + T ) = f(x + mT ) = f(x). Тому, згiдно з принципом математично¨ iндукцi¨ число nT; n 2 N, ¹ перiодом функцi¨ f. Аналогiчнi мiркування слiд провести i для вiд'¹мних n 2 Z: J

Найчастiше пiд перiодом функцi¨ f розумiють ¨¨ найменший додатний перiод, який називають основним.

П р и к л а д 6. 1) Функцi¨ синус i косинус ¹ перiодичними з основним перiодом T = 2 , а функцi¨ тангенс i котангенс перiодичнi

з основним перiодом T = .

2) Функцiя Дiрiхле

D(x) =

1; êîëè x 2 Q;

0; êîëè x 62Q;

перiодична; ¨¨ перiодом ¹ будь-яке рацiональне число T 6= 0. Ця функцiя не ма¹ основного перiоду.

3) Функцiя f(x) = fxg (дробова частина x, див. рис. 1.8, б )) ¹ перiодичною з основним перiодом T = 1.

1.3.5. Основнi елементарнi функцi¨

На практицi досить часто людина створю¹ та вивча¹ багато нових об'¹ктiв за допомогою незначно¨ кiлькостi так званих основних об'¹- ктiв. Це саме стосу¹ться i до функцiй, множина яких, якщо навiть обмежитися тiльки числовими функцiями, ¹ нескiнченною. Серед усiх цих функцiй видiляють вузький клас, за допомогою якого вивчають майже всi iншi функцi¨, що зустрiчаються на практицi. Тому цей клас функцiй ¹ дуже важливим i вiн носить спецiальну назву клас основних елементарних функцiй.

Основними елементарними функцiями називають такi числовi функцi¨:

стала f(x) = C; C = const;

степенева f(x) = x ; фiксоване число;

показникова f(x) = ax; 0 < a 6= 1; a фiксоване число;

логарифмiчна f(x) = loga x; 0 < a 6= 1; a фiксоване (вона ¹

оберненою до показниково¨);

тригонометричнi (f(x) = cos x, f(x) = sin x, f(x) = tg x, f(x) = ctg x);

оберненi тригонометричнi (f(x) = arccos x, f(x) = arcsin x, f(x) = arctg x, f(x) = arcctg x).

äå N0 3 n фiксоване, a0; a1; : : : ; an заданi дiйснi або комплекснi числа (коефiцi¹нти многочлена Pn(x)), Pn(x) многочлен степеня

n, ÿêùî an 6= 0.

Зокрема, при a 6= 0 квадратний тричлен f(x) = ax2 + bx+ c ¹ многочленом другого степеня (загальна квадратична функцiя ), а лiнiйна функцiя f(x) = ax + b ¹ многочленом першого степеня;

рацiональнi це функцi¨ вигляду R(x) = Pm(x) ; äå Pm(x) i

Qn(x)

Qn(x) многочлени степенiв m i n вiдповiдно, причому Qn(x) 6= 0 для деяких x. Зрозумiло, що цей клас мiстить в собi клас многочленiв.

Тому часто многочлен називають цiлою рацiональною функцi¹ю , а коли функцiя R(x) не ¹ многочленом, то ¨¨ називають дробово-рацiональною

функцi¹ю.

iррацiональнi функцi¨ це функцi¨, що не ¹ рацiональними;

алгебра¨чнi функцi¨, тобто такi функцi¨ y = f(x), якi ¹ розв'язком

рiвняння

a0 + a1y + a2y2 + + anyn = 0;

äå êîåôiöi¹íòè ak деякi заданi многочлени. Зрозумiло, що кожна рацiональна функцiя ¹ алгебра¨чною, оскiльки вона ¹ розв'язком рiвняння Pm(x) Qn(x)y = 0;

трансцендентнi функцi¨ це функцi¨, якi не ¹ алгебра¨чними. До них вiдносяться, зокрема, степенева функцiя f(x) = x ; äå 62Q, показникова f(x) = ax äå a 6= 1; a 6= 0, логарифмiчна, тригонометричнi

та оберненi тригонометричнi функцi¨.

Зауважимо, що кожну елементарну функцiю (враховуючи й основнi елементарнi) дiйсно¨ змiнно¨ x можна розглядати i як функцiю компле-

êñíî¨ çìiííî¨ z.

П р и к л а д 9. 1) Функцiя f(x) = x3 5x + 6 ¹ многочленом;

x2 1

2) f(x) = x2 + 1 дробово-рацiональна функцiя; p

3) f(x) = x iррацiональна алгебра¨чна функцiя (вона ¹ розв'язком рiвняння y2 x = 0);

4) f(x) = sin2 x; f(x) = 2x2 трансцендентнi функцi¨.

П р и к л а д 10. Замiсть кожно¨ функцi¨ f(x) з прикладу 9

можна розглядати вiдповiдну функцiю комплексно¨ змiнно¨, наприклад f(z) = z3 5z + 6 многочлен, f(z) = 2z2 трансцендентна функцiя

комплексно¨ змiнно¨.