
ifmion_kma_Mykhalin_Dujenkova(Mnozhyny)
.pdf1.3..Найпростiшi властивостi та класифiкацiя числових функцiй. 31
1.3.8. Iстoрична довiдка
Введена нами класифiкацiя функцiй навiяна вiдповiдною класифiкацi¹ю дiйсних чисел. Вiдповiднi поняття по сутi сформувалися в роботах французького математика Р. Декарта та швейцарського матема-
тика Л. Ейлера. Термiни "алгебра\, "алгебра¨чний\ походять вiд арабського "аль джебр\ арабським математиком аль-Хорезмi (787 850). Термiн "трансцендентний\ походить вiд латинського transcendentis
"що виходить за межi\.
1.3.9. Зв'язок iз шкiльним курсом математики
Наведенi у цьому параграфi найпростiшi властивостi функцiй разом з поняттями областi визначення та множини значень функцi¨ становлять мiнiмальну схему повного дослiдження функцi¨, чим повинен володiти кожен вчитель математики.
У багатьох випадках це дослiдження можна проводити елементарними засобами, тобто користуючись лише вiдповiдними означеннями. На нашу думку, таке дослiдження без використання засобiв диференцiального числення да¹ змогу вчителевi глибше зрозумiти вiдповiднi
властивостi функцiй, а отже, й краще донести ¨х до учнiв.
1.3.10. Постановка проблем
Поки що серед основних елементарних функiй фактично визначенi лише стала та степенева функцiя з цiлим показником.
Тому основною проблемою залиша¹ться проблема означення iнших
основних елементарних функцiй як дiйсно¨, так i комплексно¨ змiнно¨.
1.3.11. Контрольнi запитання та завдання
1. Перевiрити, чи правильними ¹ такi твердження:
1)кожна строго монотонна функцiя ¹ монотонною;
2)якщо функцiя f незростаюча на множинi A, то вона спадна на
цiй множинi;
3)твердження, обернене до 2), ¹ правильним;
4)сума, рiзниця, добуток та частка монотонних функцiй ¹ функцi¹ю монотонною;
5)кожна функцiя ¹ або парною, або непарною;
6)кожну функцiю можна подати у виглядi суми парно¨ та непарно¨ функцiй;
7)iсну¹ функцiя, яка одночасно ¹ i парною, i непарною;
8)áóäü-ÿêà монотонна функцiя не ¹ перiодичною;
9)кожна строго монотонна функцiя не ¹ перiодичною;
10)iсну¹ функцiя, вiдмiннa вiд стало¨, для яко¨ кожне дiйсне число
¹ïåðiîäîì;
11)кожна основна елементарна функцiя ма¹ промiжки монотонно-
ñòi;
12)кожний многочлен ¹ монотонною функцi¹ю;
32 |
Роздiл 1. Елементарнi факти теорi¨ множин |
13)кожний многочлен не ¹ перiодичною функцi¹ю;
14)ÿêùî f многочлен, то f рацiональна функцiя;
15)твердження, обернене до 14), ¹ правильним;
16)сума, рiзниця, добуток i частка рацiональних функцiй ¹ функцi¹ю рацiональною;
17)функцiя f(x) = 1=x ¹ монотонною дробово-рацiональною фун-
кцi¹ю, що ма¹ два промiжки спадання. 2. Довести данi твердження:
1)суперпозицiя двох монотонних функцiй (якщо вона iсну¹) ¹ монотонною функцi¹ю;
2)суперпозицiя двох функцiй (якщо вона iсну¹), одна з яких парна,
àдруга непарна, ¹ парною функцi¹ю;
3)якщо функцiя, вiдмiнна вiд стало¨, ¹ перiодичною, то вона не ¹ монотонною.
1.4. Еквiвалентнi множини та потужностi множин
Вводяться поняття еквiвалентних множин, скiнченних та нескiн- ченних множин, кiлькостi елементiв, або потужностi множин. Розгляда¹ться питання про порiвняння потужностей, зокрема теорема Кантора Бернштейна.
1.4.1. Еквiвалентнi множини
Однi¹ю iз задач, якi привели до поняття числа, ¹ задача визначення кiлькостi елементiв дано¨ множини. Вона розв'зу¹ться пiдрахунком цих
елементiв. Так, множина A = fa; b; cg ма¹ три елементи i ¨х бiльше, нiж у множини B = fx; yg.
Однак процедура пiдрахунку кiлькостi елементiв годиться лише для так званих скiнченних множин. А що треба розумiти пiд "êiëüêiñòþ
елементiв нескiнченно¨ множини , зокрема множин N, Z, Q, R i C?
Як можна порiвнювати цi множини за кiлькiстю елементiв? Вiдповiсти на це питання допоможе зауваження про те, що в про-
цесi пiдрахунку елементiв скiнченно¨ множини по сутi визнача¹ться вза¹мно однозначне вiдображення деяко¨ пiдмножини множини натуральних чисел на задану скiнченну множину.
П р и к л а д 1. Пiдраховуючи кiлькiсть елементiв множини A = fa; b; cg, можна числу 1 поставити у вiдповiднiсть елемент a, числу
2 елемент b, а числу 3 елемент c, тобто вказати вза¹мно однозначну вiдповiднiсть f : f1; 2; 3g $ fa; b; cg.
У зв'язку з цим вводять таке означення.
Означення 1 (е к в i в а л е н т н и х м н о ж и н). Множини A i B називають еквiвалентними i записують A B, якщо iсну¹ вза¹мно
1.4. Еквiвалентнi множини та потужностi множин |
33 |
однозначне вiдображення множини A на множину B. Отже, A B , 9f : A $ B.
В iншому разi множини A i B називають нееквiвалентними i записують A 6 B.
П р и к л а д 2. 1) За даним означенням множини A = fa; b; cg
iC = fx; yg нееквiвалентнi: fa; b; cg 6 x;f yg.
2)A = f1; 2; : : : ; n; : : : g i B = f2; 4; : : : ; 2n; : : : g ¹ еквiвалентними, оскiльки формула f(x) = 2x зада¹ вза¹мно однозначне вiдображення
множини A на множину B, в чому легко переконатися.
За означенням вважають, що ? ?.
Тепер можна дати чiтке означення скiнченно¨ та нескiнченно¨ множин.
Означення 2 (с к i н ч е н н о ¨ т а н е с к i н ч е н н о ¨ м н о ж и н). Множину A називають скiнченною, якщо вона або порожня, або iсну¹
таке натуральне число n, що A f1; 2; 3; : : : ng. При цьому кажуть, що множина A ма¹ вiдповiдно або нуль елементiв, або n елементiв. Множину, яка не ¹ скiнченною, називають нескiнченною.
1.4.2. Властивостi еквiвалентних множин
Вкажемо на основнi властивостi еквiвалентних множин.
1)Рефлексивнiсть: A A;
2)симетричнiсть: A B =) B A;
3)транзитивнiсть: A B i B C =) A C;
4)еквiвалентнiсть об'¹днань . Нехай Ai Bi 8i 2 I (I множина
iндексiв), причому Ai \ Ak = ? i Bi \ Bk = ?, êîëè i 6= k. Òîäi |
|
S |
S |
Ai Bi.
ii
Проiлюстру¹мо методи доведення цих властивостей на прикладi
властивостi 4). |
|
таке вiдображенняSf множини ASна всю множину B, при якому ко- |
|
I Нехай A = Ai, a B = |
Bi. Треба довести, що знайдеться |
i2I |
i2I |
жним двом рiзним елементам з множини A вiдповiдають два рiзнi елементи з множини B.
Оскiльки Ai Bi, то 9fi : Ai $ Bi 8i 2 I. За умовою множини Ai не перетинаються, тому 8x 2 A 9! i 2 I : x 2 Ai. Покладемо f(x) := fi(x). Тодi fi(x) 2 Bi, а тому f(x) 2 B, тобто f : A ! B.
Покажемо, що функцiя f вiдобража¹ множину A на всю множину |
||
|
Bi попарно не перетинаються, |
S |
B. Для цього вiзьмемо довiльне y 2 B тобто y 2 Bi, i враховуючи, |
||
що множини |
|
i2I |
|
äiñòà¹ìî: |
|
9! i 2 I : y 2 Bi ) 9 x 2 Ai : y = fi(x) ) 9 x 2 A : y = f(x):
34 Роздiл 1. Елементарнi факти теорi¨ множин
Îòæå, f : A íà B.
!
Нехай x1 6= x2 довiльнi елементи з A. Òîäi, ÿêùî x1 i x2 належать до однi¹¨ множини Ai, òî f(x1) = fi(x1) 6= fi(x2) = f(x2), îñêiëüêè fi : Ai $ Bi. À êîëè x1 i x2 належать рiзним множинам
Ai, наприклад x1 2 Ai1 a x2 2 Ai2 ; i1 6= i2, òî f(x1) = fi1 (x1) 2 Bi1 , à f(x2) = fi2 (x2) 2 Bi2 . Враховуючи, що множини Bi1 i Bi2 íå ïåðå- тинаються, дiста¹мо f(x1) 6= f(x2).
Таким чином, f : A $ B i òîìó A B. J
Зауважимо, що коли у властивостi 4) не вимагати, щоб множини Ai (Bi) не перетиналися, то це твердження ста¹ неправильним.
Ï ð è ê ë à ä 3. ßêùî A1 = f1g i A2 = f1g; B1 = f2g i
B2 = f3g, òî A1 B1; A2 B2, проте A1[A2 = f1g 6 2f; 3g = B1[B2.
Iншi властивостi еквiвалентних множин пропону¹мо читачевi довести самостiйно.
1.4.3. Поняття кiлькостi елементiв, або потужностi множини
ßêùî A фiксована множина, то можна утворити клас усiх множин, еквiвалентних множинi A. При цьому, якщо множина B 6 A, то вона утворю¹ iнший клас еквiвалентних множин (еквiвалентних множинi B). Тому можна вважати, що кожна множина попада¹ в один i
тiльки один клас еквiвалентних множин. Зокрема, порожня множина ? попада¹ в клас, який мiстить тiльки ¨¨ одну. Множина f1g íàëå-
жить класу множин, кожна з яких ма¹ один елемент; множина f1; 2g
класу двоелементних множин тощо.
Óзв'язку з цим природно дати таке означення кiлькостi елементiв довiльно¨ множини.
Означення 3 (к i л ь к о с т i е л е м е н т i в, а б о п о т у ж н о с т i м н о - ж и н). Кiлькiстю елементiв або потужнiстю множини A назива-
ють деякий символ (A), який приписують класу множин, кожна з яких еквiвалентна множинi A. При цьому кажуть, що множина A
ма¹ (A) елементiв або ма¹ потужнiсть (A).
З цього означення виплива¹, що для будь-яко¨ скiнченно¨ множини A ¨¨ потужнiстю можна назвати або число нуль, коли A = ?, àáî íàòó-
ральне число n, ÿêùî A f1; 2; : : : ; ng. Отже, скiнченна потужнiсть
це звичайна числова кiлькiсть елементiв вiдповiдно¨ множини. Якщо множина A нескiнченна, то кажуть, що вона ма¹ íåñêií÷åí-
ну кiлькiсть елементiв àáî нескiнченну потужнiсть. Зокрема, потужнiсть (N) множини натуральних чисел називають зчисленною (ç÷è-
сленною кiлькiстю елементiв ) i позначають a, а потужнiсть вiдрiзка
[0; 1] називають континуальною (континуальною кiлькiстю елемен-
òiâ) i позначають c.
Зауважимо, що означення скiнченно¨ множини збiга¹ться з iнту¨- тивним уявленням про скiнченнi множини. Бiльше того, воно сфор-
1.4. Еквiвалентнi множини та потужностi множин |
35 |
мульоване на основi цих уявлень. Дiйсно, сам процес пiдрахунку елементiв деяко¨ скiнченно¨ множини A 6= ? поляга¹ в тому, що ми пере-
бира¹мо елементи цi¹¨ множини по порядку i ставимо кожному з них у вiдповiднiсть певний номер (натуральне число). При цьому елемен-
òó a 2 A ми ставимо у вiдповiднiсть ¹дине натуральне число, причо- му рiзним a i b 2 A у вiдповiднiсть ставляться рiзнi натуральнi чи- сла, тобто фактично встановлю¹ться вза¹мно однозначне вiдображення f : A $ f1; 2; : : : ; ng.
За властивiстю транзитивностi еквiвалентних множин ма¹ мiсце таке твердження.
Теорема 1 (п р о е к в i в а л е н т н i с т ь с к i н ч е н н и х м н ож и н).
Скiнченнi множини A i B еквiвалентнi тодi й тiльки тодi, коли вони мають однакову кiлькiсть елементiв.
1.4.4. Порiвняння потужностей (кiлькостi елементiв) множин
Скiнченнi потужностi можна порiвнювати мiж собою:
(fa; b; cg) = 3 > (fx; yg) = 2, (f1; 2g) = (fx; yg) = 2.
За аналогi¹ю iз скiнченними множинами можна ввести такi озна- чення.
Для даних множин A i B кажуть, що:
âîíè мають однаковi потужностi i записують (A) = (B), ÿêùî A B;
потужнiсть A менша за потужнiсть B i записують (A) <
(B), ÿêùî A 6B, однак iсну¹ така пiдмножина B1 B, ùî A B1;
потужнiсть A бiльша за потужнiсть B i записують (A) >(B), ÿêùî (B) < (A);
потужнiсть A не бiльша за потужнiсть B i записують (A)
(B), ÿêùî (A) < (B) àáî (A) = (B);
потужнiсть A не менша за потужнiсть B i записують (A)
(B), ÿêùî (A) > (B) àáî (A) = (B).
ßêùî (A) i (B) скiнченнi потужностi, то за властивостями дiйсних чисел з нерiвностей (A) (B) i (A) (B) виплива¹ рiвнiсть (A) = (B).
Природно чекати, що ця властивiсть ма¹ мiсце i для нескiнченних потужностей. Спробу¹мо це довести.
I Îñêiëüêè (A) > (B), то iсну¹ така множина A1, ùî A A1 B, тобто iсну¹ вза¹мно однозначне вiдображення ' множини B на множину A1. З нерiвностi (A) 6 (B) виплива¹ iснування тако¨ множини B1, ùî B B1 A.
Позначимо '(B1) = A2 A1 i дiстанемо включення A A1 A2, a з еквiвалентностей A B1 i A2 B1 äiñòà¹ìî, ùî A A2.
Îòæå, A A1 A2 i A A2.
36 |
Ðîçäië 1. |
Елементарнi факти теорi¨ множин |
||||||
Якщо покажемо, що звiдси виплива¹ еквiвалентнiсть |
A A1, òî |
|||||||
за властивiстю транзитивностi з урахуванням еквiвалентностi A1 B |
||||||||
дiстанемо, що |
A B, тобто (A) = (B). |
|
|
|
|
|
||
Îñêiëüêè |
A A2, то iсну¹ вза¹мно однозначне вiдображення f |
|||||||
множини A íà A2. |
|
|
|
|
|
|
|
|
|
|
|
|
Позначимо f(A1) = A3 A2, |
||||
|
|
f(A2) = A4 A3 i, взагалi, f(An) = |
||||||
|
|
An+2 An+1 8n 2 N0, äå A0 := |
||||||
|
|
A. |
|
|
|
|
|
|
|
|
|
|
Тодi дiстанемо, що f âçà¹ì- |
||||
|
|
но однозначно вiдобража¹ мно- |
||||||
|
|
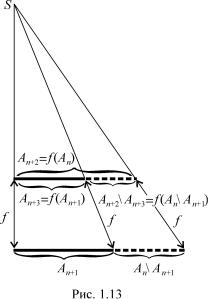
æèíó An íà An+2 |
i An n An+1 |
|||||
|
|
íà An+2 n An+3 (ðèñ. 1.13), òîá- |
||||||
|
|
òî An An+2 i An n An+1 |
||||||
|
|
An+2 n An+3. |
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Нехай X = |
An, |
|
||
|
|
|
|
1 |
=0 |
|
|
|
|
|
|
|
nT |
|
|
||
|
|
Y = n=0(A2n+1 n A2n+2), Z1 = |
||||||
|
|
1 |
S |
|
1 |
|
||
|
|
n=0(A2nnA2n+1), Z2 = n=0 A2n+2n |
||||||
|
|
|
A |
. |
|
S |
|
|
|
|
S2n+3 |
|
|
|
|||
|
|
n |
|
Покажемо, що A = X [ Y [ |
||||
|
|
|
|
|||||
|
|
Z1 i A1 = X [ Y [ Z2. |
|
|||||
|
|
|
|
Äiéñíî, x 2 A |
, x 2 An |
|||
An0 i x 62An0+1 , x 2 X àáî |
8n 2 N0 àáî |
9 n0 |
2 N0 : x 2 |
|||||
x 2 An0 n An0+1 , x 2 X àáî |
x 2 Y , |
|||||||
ÿêùî n0 непарне число, або |
x 2 Z1, êîëè n0 парне. |
|
|
|||||
Цим доведено рiвнiсть A = X [ Y [ Z1. |
|
|
|
|
||||
Ðiâíiñòü A1 = X [ Y [ Z2 доводиться аналогiчно. |
|
|
An n |
|||||
Оскiльки об'¹днуванi множини попарно не перетинаються i |
||||||||
An+1 An+2 n An+3 8n 2 N0, то за властивiстю 4) еквiвалентних |
||||||||
множин спочатку дiста¹мо, що |
Z1 Z2, a ïîòiì |
i A1 B, à òîìó |
||||||
X [Y [Z1 X [Y [Z2 = A1, тобто A A1. A A1 |
||||||||
A B. J |
|
|
|
|
|
|
|
|
Отже, доведено таке твердження.
Теорема 2 (К а н т о р а Б е р н ш т е й н а). ßêùî (A) (B) i
(A) (B) òî (A) = (B).
Наступне важливе твердження приймемо без доведення.
Теорема 3 (п р о п о р i в н я н н я п о т у ж н о с т е й). Для будь-яких множин A i B ма¹ мiсце одне й тiльки одне iз спiввiдношень: або
(A) = (B), àáî (A) < (B), àáî (A) > (B).
1.4. Еквiвалентнi множини та потужностi множин |
37 |
1.4.5. Iсторична довiдка
Поняття потужностi множини та основнi твердження про потужностi множин належать нiмецькому математику Г. Кантору.
1.4.6. Зв'язок iз шкiльним курсом математики
Не зважаючи на те, що поняття потужностi множини не вивча¹ться у шкiльному курсi математики, вчитель математики повинен ним володiти, оскiльки повинен розумiти, що таке скiнченна та нескiнченна множина, i знати, яких чисел бiльше: цiлих чи натуральних, натуральних чи рацiональних, рацiональних чи дiйсних, дiйсних чи комплексних.
На перший погляд зда¹ться, що цiлих чисел бiльше нiж натуральних, оскiльки N Z i N 6= Z. Однак, даючи таку вiдповiдь, необ-
грунтовано переносять властивостi скiнченних множин на нескiнченнi множини.
Насправдi, якщо пiд кiлькiстю елементiв нескiнченно¨ множини розумiти ¨¨ потужнiсть, то як буде нижче показано, натуральних чисел ¹ стiльки ж, скiльки цiлих i рацiональних, проте менше нiж дiйсних, а дiйсних чисел ¹ стiльки, скiльки й комплексних.
1.4.7. Постановка проблем
Основною проблемою, яку буде розв'язано в наступному параграфi, ¹ проблема порiвняння потужностей множин N; Z, Q; R i C.
1.4.8. Контрольнi запитання та завдання
1. Перевiрити, чи правильними ¹ такi твердження:
1)скiнченнi множини еквiвалентнi тодi й тiльки тодi, коли вони мають однакову кiлькiсть елементiв;
2)ÿêùî A1 B1 i A2 B2, òî A1 [ A2 B1 [ B2;
3)ÿêùî A B i A 6= B, òî A 6 B;
4)якщо множина A нескiнченна, то вона еквiвалентна деякiй сво¨й
власнiй пiдмножинi;
5)твердження, обернене до 4), ¹ правильним;
6)ÿêùî A 6 B i B 6 C, òî A 6 C;
7)ÿêùî A власна пiдмножина B, òî (A) < (B);
8)ÿêùî A i B скiнченнi множини, то (A[B) = (A)+ (B) ,
A \ B = ?;
9)iсну¹ найменша потужнiсть;
10)зчисленна потужнiсть бiльша за будь-яку скiнченну.
2. Довести данi твердження:
1)ÿêùî a < b i c < d, òî 9 f : [a; b] $ [c; d], тобто áóäü-ÿêi невиродженi вiдрiзки еквiвалентнi мiж собою;
2)ÿêùî A нескiнченна множина i a 2 A, òî Anfag A; зокрема,
ÿêùî a < b, òî [a; b] (a; b];
3) будь-якi невиродженi числовi промiжки еквiвалентнi мiж собою.

38 |
Роздiл 1. Елементарнi факти теорi¨ множин |
1.5. Зчисленнi множини
Розгляда¹ться важливий клас зчисленних множин та ¨хнi властивостi. Показано, що множини цiлих, рацiональних та алгебра¨чних чисел ¹ зчисленними.
1.5.1. Поняття зчисленно¨ множини та ¨¨ критерiй
Означення 1 (п о т у ж н о с т i м н о ж и н и N). Кiлькiсть елементiв (потужнiсть) множини N = f1; 2; 3; : : : ; n; : : : g натуральних чисел називають зчисленною i позначають лiтерою a, тобто (N) = a.
Означення 2 (з ч и с л е н н о ¨ м н о ж и н и). Множину A називають
зчисленною, якщо вона еквiвалентна множинi натуральних чисел N,
тобто якщо вона ма¹ зчисленну кiлькiсть елементiв (зчисленну потужнiсть).
П р и к л а д 1. Множина A = f2; 4; : : : ; 2n; : : : g ¹ зчисленною, тобто (A) = a, îñêiëüêè A N.
I Нехай A зчисленна множина, тобто A N, àáî N A. Це означа¹, що iсну¹ вза¹мно однозначне вiдображення f множини N íà A, тобто виконуються умови:
1) 8n 2 N 9! x = f(n) = xn 2 A;
2) xn1 = f(n1) 6= f(n2) = xn2 8n1 6= n2;
3) 8x 2 A 9n 2 N : x = f(n) = xn.
Останн¹ рiвносильнe тому, що множину A можна записати у виглядi множини членiв деяко¨ послiдовностi, тобто A = fx1; x2; : : : ;
xn; : : : g, причому члени цi¹¨ послiдовностi попарно рiзнi ( xn1 6= xn2 , êîëè n1 6= n2). У цьому випадку кажуть, що елементи множини A
занумеровано всiма натуральними числами . J
Отже, доведено таке твердження.
Теорема 1 (к р и т е р i й з ч и с л е н н о с т i). Для того щоб множина A була зчисленною, необхiдно й досить, щоб ¨¨ елементи можна
було занумерувати всiма натуральними числами, тобто подати A у виглядi множини попарно рiзних членiв деяко¨ послiдовностi.
Множину f1; 2; 3; : : : ; ng =: 1; n називають вiдрiзком множини на-
туральних чисел. Зрозумiло, що кожну скiнченну множину можна занумерувати всiма натуральними числами якогось вiдрiзка множини натуральних чисел.
1.5.2. Найменша нескiнченна потужнiсть
Множину A називають не бiльш нiж зчисленною, якщо вона ¹ або скiнченною, або зчисленною, тобто (A) a. При цьому замiсть слiв
"не бiльш нiж зчисленна потужнiсть"вживають слова "не бiльш нiж зчисленна кiлькiсть". Зрозумiло, що елементи не бiльш нiж зчисленно¨ множини, вiдмiнно¨ вiд порожньо¨, можна занумерувати або скiнченною кiлькiстю натуральних чисел, або всiма натуральними числами.
1.5. Зчисленнi множини |
39 |
Вiдомо, що кожна скiнченна потужнiсть менша за зчисленну. Виника¹ питання, чи iсну¹ нескiнченна потужнiсть, менша за зчисленну.
I Зрозумiло, що коли нескiнченна множина B ¹ пiдмножиною зчи- сленно¨ множини A = fa1; a2; : : : ; an; : : : g, то елементи множини B матимуть певнi номери: B = fan1 ; an2 ; : : : ; ank ; : : : g.
Тому за теоремою 1 множина B ¹ зчисленною, тобто ма¹ мiсце таке твердження. J
Теорема 2 (п р о п о т у ж н i с т ь н е с к i н ч е н н о ¨ п i д м н ож и н и з ч и с л е н н о ¨ м н о ж и н и).
но¨ множини також ¹ зчисленною .
I Припустимо тепер, що iсну¹ нескiнченна потужнiсть, менша за
зчисленну.
Тодi iсну¹ нескiнченна множина A òàêà, ùî (A) < a, тобто A 6 N, проте A B1 N, äå B1 нескiнченна множина.
За теоремою 2 множина B1 ¹ зчисленною, а тому й множина A B
також зчисленна
Отже, припущення про iснування нескiнченно¨ потужностi, меншо¨ за зчисленну, неправильне, i тому доведено таке твердження. J
Теорема 3 (п р о н а й м е н ш у н е с к i н ч е н н у п о т у ж н i с т ь).
Зчисленна потужнiсть ¹ найменшою серед усiх нескiнченних потужностей, тобто (N) 6 (A), якщо A нескiнченна множина.
1.5.3. Об'¹днання не бiльш нiж зчисленних множин
Неважко помiтити, що скiнченну множину бiльшо¨ потужностi можна дiстати об'¹днанням множин меншо¨ потужностi.
Виника¹ питання, чи можна об'¹днанням не бiльш нiж зчисленно¨ кiлькостi зчисленних множин Ai дiстати множину, потужнiсть яко¨ бiльша за зчисленну.
I Щоб вiдповiсти на це питання, зауважимо, що елементи множини
Iiндексiв можна занумерувати або всiма натуральними числами, i тодi
I= fi1; i2; i3; : : : g, або деяким вiдрiзком множини натуральних чисел, i тодi I = fi1; i2; i3; : : : ; ing.
Кожна множина Aik за умовоюn¹ íå ¨¨ можна записати у виглядi: Aik = a(1k)
бiльш нiж зчисленноюo . Òîìó
; a(2k); a(3k); : : : .
Пiсля цього можна переписати елементи всiх множин Aik у виглядi тако¨ таблицi:
a1(1); |
a2(1); |
a3(1); |
: : : |
|
a1(2); |
a2(2); |
a3(2); : : : |
(1.1) |
|
a1(3); |
a2(3); |
a3(3); |
|
|
: : : |
|
|||
: : : |
: : : |
: : : |
: : : |
|
40 |
Роздiл 1. Елементарнi факти теорi¨ множин |
Якщо в якомусь рядку таблицi (1) скiнченна кiлькiсть елементiв, то вважатимемо, що останнiй елемент повторю¹ться зчисленну кiлькiсть разiв. Якщо кiлькiсть рядкiв таблицi (1) скiнченна, то вважатимемо, що останнiй рядок повторю¹ться зчисленну кiлькiсть разiв.
Тепер занумеру¹мо елементи таблицi (1) за схемою
1 |
3 |
4 |
10 |
: : : |
2 |
5 |
9 |
: |
: : : |
6 |
8 |
: |
: |
: : : |
7: : : : : :
При цьому, якщо зустрiча¹ться елемент, який вже занумеровано, то
його пропуска¹мо. |
S Ai ¹ елементами табли- |
Оскiльки всi елементи множини A = |
i2I
цi (1), то вони занумерованi або всiма натуральними числами, або ¨х скiнченною кiлькiстю. Тому A не бiльш нiж зчисленна множина, а
ÿêùî A нескiнченна, то за теоремою 2 вона ¹ зчисленною. J Отже, доведено таке твердження.
Теорема 4 (п р о о б'¹ д н а н н я н е б i л ь ш н i ж з ч и с л е н н и х м н о ж и н). Об'¹днання не бiльш нiж зчисленно¨ кiлькостi не бiльш нiж зчисленних множин ¹ не бiльш нiж зчисленною множиною. Якщо
це об'¹днання ¹ нескiнченною множиною, то воно зчисленне.
Пропону¹мо читачевi з теореми 4 дiстати наслiдки про потужнiсть об'¹днання:
1)зчисленно¨ кiлькостi скiнченних множин;
2)скiнченно¨ кiлькостi зчисленних множин;
3)зчисленно¨ кiлькостi зчисленних множин.
1.5.4. Потужнiсть множин Z i Q
За допомогою теореми 3 неважко розв'язати питання про поту-
жнiсть множин N0 |
= f0; 1; 2; 3; : : : g, N = f 1; 2; 3; : : : g, Z = |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f0; 1; 1; 2; 2; 3; 3; : : : g i Q = |
|
|
|
: m 2 Z; n 2 N . |
|
|
|
|
|
|
|
|||||||||||||||||||
|
n |
|
|
|
|
|
|
|
||||||||||||||||||||||
Îñêiëüêè N0 = N |
0 |
|
|
|
за теоремою 4 ма¹мо |
N0 |
|
|
N |
, тобто |
||||||||||||||||||||
, òî n |
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
||||||||||||||
|
|
|
|
[ f g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
N0 зчисленна множина. |
|
|
|
|
|
|
|
|
|
|
|
|
f : N ! N , що визнача- |
|||||||||||||||||
Неважко помiтити, що вiдображення |
||||||||||||||||||||||||||||||
¹ться формулою f(n) = n ¹ вза¹мно однозначним. Тому |
|
N N, |
||||||||||||||||||||||||||||
тобто N зчисленна множина. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Враховуючи, що |
Z = N0 [ N, знову ж таки з теорeми 4 виплива¹, |
|||||||||||||||||||||||||||||
ùî Z зчисленна множина. |
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|||||||
За означенням множини |
|
|
ìà¹ìî: |
|
|
|
|
|
|
|
|
|
n |
|
|
N |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
Q |
|
|
|
m |
|
Q = n n : m 2 Z; m |
2 |
|
o. |
|||||||||||||||
Розглянемо множини |
|
|
|
|
|
|
|
|
|
|
m |
|
Z , |
Q |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
n 1 |
|
|
|
= n 2 |
|
: m 2 Zo, |
||||||||||||||||||||
m |
|
|
Q1 |
= |
: m |
2 |
o |
|
2 |
|
||||||||||||||||||||
Q3 = n |
|
: m 2 Zo |
i взагалi |
|
Qk = |
n |
|
|
: m 2 Zo, |
де k ¹ довiльним |
||||||||||||||||||||
3 |
|
k |
||||||||||||||||||||||||||||
фiксованим натуральним числом. Зрозумiло, що кожна з цих множин
