
ifmion_kma_Mykhalin_Dujenkova(Mnozhyny)
.pdf
1.2. Поняття вiдповiдностi, вiдображення, функцi¨ |
11 |
1.1.8. Контрольнi запитання та завдання
1. Перевiрити, чи правильними ¹ такi твердження:
1)твердження "Множина це багато чогось, на що можна дивитись як на щось цiле"¹ означенням;
2)A = ? , A B 8B;
3)A B , 9 x 2 A : x 2 B;
4)A B , x 62B 8x 62A;
5)iсну¹ множина, усi пiдмножини яко¨ невласнi;
6)x 62A [ B , x 62A àáî x 62B;
7)x 62A \ B , x 62A i x 62B;
8)x 62A n B , x 62A àáî x 2 B;
9)x 62CE(A [ B) , x 62CEA àáî x 62CEB;
10)x 62CE(A \ B) , x 62CEA i x 62CEB.
2. Знайти об'¹днання, перерiз та рiзницю множин A i B:
1)A = fx 2 R : xx + 12 > 1g; B = ( 1; 2);
2)A = fx 2 R : x2 5x + 6 > 0g; B = f2; 3; 4g. x 4
3. |
Знайти об'¹днання та перерiз множин Yn; n 2 N: |
|||||||||||||
1) |
Yn = h n; |
ni; |
2) Yn = (0; n]; |
3) Yn = nno; |
||||||||||
|
1 |
|
1 |
|
|
1 |
|
1 |
|
|||||
|
|
|
|
n |
5) Yn = ( |
|
n |
|
|
n |
||||
4) |
Yn = (0; |
|
); |
|
; |
|
). |
|||||||
n 1 |
n + 1 |
2n + 1 |
||||||||||||
4. Непорожню множину S деяких пiдмножин унiверсально¨ множини називають алгеброю ( -алгеброю), якщо: а) A 2 S, коли A 2 S
|
n |
|
1 |
i á) |
S |
|
iS |
i=1 Ai 2 S |
8n 2 N ( |
=1 Ai 2 S), êîëè Ai 2 S. |
Довести, що -алгебра ¹ алгеброю, причому:
TS
1) 2 S i ? 2 S; 2) Ai = Ai;
ii
3)Tn Ai 2 S (для алгебри) i T1 Ai 2 S (для -алгебри);
i=1 |
i=1 |
||
4) A n B = A T |
|
; |
5) A n B 2 S, ÿêùî A; B 2 S. |
B |
|||
1.2. Поняття вiдповiдностi, вiдображення, функцi¨
Розглядаються означення функцi¨ як вiдповiдностi мiж множинами та залежностi мiж змiнними, якi грунтуються на одному й тому самому поняттi множини та ¨¨ елементiв. Наведено приклади функцiй, якi надалi часто використовуватимуться. Введено поняття обернено¨ та складно¨ функцiй.

12 |
Роздiл 1. Елементарнi факти теорi¨ множин |
1.2.1.Деякi зауваження щодо введення поняття функцi¨
Поняття функцi¨ одне з найважливiших математичних понять. Досить часто його визначають як залежнiсть одних змiнних величин вiд iнших.
Величезна кiлькiсть практичних задач приводить до поняття функцi¨ та розв'язу¹ться за допомогою саме цього поняття.
П р и к л а д 1. 1) Площа S прямокутника ¹ функцi¹ю його сторiн x i y: S = xy; 2) øëÿõ s, пройдений тiлом зi сталою швидкiстю v ¹ функцi¹ю часу t: s = vt; 3) величина сили F , з якою матерiальнi
точки масою m1 i m2 притягуються одна до одно¨, ¹ функцi¹ю вiдстанi r мiж цими точками: F = k m1m2
r2 .
Однак, якщо проаналiзувати наведене вище поняття, то виникають питання: 1) що розумiти пiд поняттям "залежнiсть\ òà 2) ùî òàêå
"змiнна величина\ i "величина\ взагалi.
Введемо поняття функцi¨, користуючись лише вже введеними поняттями множини, ¨¨ елемента та належностi елемента до множини.
1.2.2. Пари елементiв
Нехай задано двi непорожнi множини A i B. Òîäi впорядкованою
парою (або просто парою) елементiв цих множин називають множину fx; fygg, äå x фiксований елемент однi¹¨ множини, наприклад
A, à y фiксований елемент iншо¨ множини, наприклад B. Вказану множину, тобто пару, позначають (x; y), àáî (x; y), i називають x
першою, à y другою координатою (компонентою) ïàðè.
З а у в а ж е н н я. Множина fx; xg = fxg не ¹ парою на вiдмiну вiд множини fx; fxgg, що ¹ парою (x; x).
Ï ð è ê ë à ä 2. ßêùî A = f1; 2g, à B = f3; 4g, то можливi такi пари: (1; 3), (1; 4), (2; 3), (2; 4), (3; 1), (3; 2), (4; 1) i (4; 2).
Ïàðè (x; y) òà (z; u) називають рiвними i записують (x; y) = (z; u), ÿêùî x = z i y = u. Зокрема, (x; y) = (y; x) , x = y.
1.2.3. Поняття декартового добутку множин
Декартовим добутком непорожнiх множин A i B називають множину A B = f(x; y) : x 2 A; y 2 Bg , тобто множину всiх можливих пар (x; y), äå x 2 A, à y 2 B.
Ï ð è ê ë à ä 3. ßêùî A = f1; 2g, à B = f3; 4g, òî A B = f(x; y) : x 2 A; y 2 Bg = f(1; 3); (1; 4); (2; 3), (2; 4)g, à B A = f(x; y) : x 2 B; y 2 Ag = f(3; 1); (3; 2), (4; 1); (4; 2)g.
Отже, взагалi кажучи, A B 6= B A.
1.2. Поняття вiдповiдностi, вiдображення, функцi¨ |
|
|
|
|
|
|
|
|
13 |
|||||||||||||||||
Якщо непорожнi множини A i |
B рiвнi, то ¨х декартiв добуток |
|||||||||||||||||||||||||
позначають A2, |
тобто |
A |
|
A =: A2. Зокрема, R2 := R |
|
R; R3 := |
||||||||||||||||||||
|
2 i при цьому |
вважають, що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
R R |
|
|
|
|
|
|
|
|
|
f |
y; |
f |
z |
gg |
). |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
)) =: (x; y; z) = (x; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(x; (y; z n |
з елементами |
|
|
|
|
|
|
||||||||
Припустимо, що визначенo множину R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(x1; x2; : : : ; xn). Тодi покладемо Rn+1 := R Rn i |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
(x1; (x2; : : : ; xn; xn+1)) =: (x1; x2; : : : ; xn; xn+1): |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Згiдно а принципом математично¨ iндукцi¨ множина |
Rn визначена |
|||||||||||||||||||||||||
8n 2 N. Цю множину називають |
|
n-вимiрним простором, елементи |
||||||||||||||||||||||||
x = (x |
|
; x |
|
; : : : ; x |
|
) точками цього простору, à x |
2 |
R (k |
|
2 |
|
|
||||||||||||||
1 |
2 |
n |
|
1; n) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
n |
|||||||
k-îþ координатою точки x. Зрозумiло, що в мiркуваннях щодо R |
|
|
||||||||||||||||||||||||
можна замiсть R взяти довiльну множину A = ?. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Геометрично простiр R1 зображу¹ться |
числовою або координа- |
|||||||||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
тною прямою (рис. 1.2, a)), |
простiр |
R2 координатною площиною |
||||||||||||||||||||||||
OXY (ðèñ. 1.2, á )), а простiр R3 координатним простором |
|
OXY Z |
||||||||||||||||||||||||
(ðèñ. 1.2, â)). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Якщо для простору R1 вважати, що (x1) = x1, то дiстанемо, що
R1 = R. |
|
|
|
|
|
|
Згiдно з означенням |
n-вимiрного простору множини Rn i Rm íå- |
|||||
порiвняннi за вiдношенням включення, коли |
n 6= m. Àëå, ÿêùî ââà- |
|||||
æàòè, ùî ïðè n < m ìà¹ìî (x1; x2; : : : ; xn) = (x1; x2; : : : ; |
||||||
xn; xn+1; : : : ; xm), äå xk = 0 8k > n, |
n |
m |
||||
1òî R 2 |
R 3 8n6m. |
|||||
домовленостi |
R |
R |
R : : : i вважають, |
|||
Зокрема, за тако¨ n, |
|
|
|
|||
|
|
|
|
|||
що точки простору R |
n 2 1; 3; мають три координати: x1; x2; x3, ÿêi |
|||||
називають вiдповiдно абсцисою, ординатою òà аплiкатою.
1.2.4. Вiдповiднiсть мiж множинами
Вiдповiднiстю (залежнiстю) мiж непорожнiми множинами A i
B називають будь-яку множину A B. При цьому, якщо пара
(x; y) 2 , то кажуть, що елемент y 2 B вiдповiда¹ елементу x 2 A. Множину називають також законом вiдповiдностi мiж множинами
Ai B, àáî залежнiстю мiж змiнними x 2 A i y 2 B.
Ïð è ê ë à ä 4. ßêùî A = f1; 2g, à B = f3; 4g, òî Ã = f(1; 3); (1; 4); (2; 3)g одна з можливих вiдповiдностей мiж множинами
Ai B.
14 Роздiл 1. Елементарнi факти теорi¨ множин
Пропону¹мо читачевi вказати всi можливi вiдповiдностi мiж цими множинами.
Серед вiдповiдностей мiж непорожнiми множинами A i B âè-
дiляють так званi функцiональнi вiдповiдностi (функцiональнi залежностi), тобто такi, коли кожному елементу x 2 A вiдповiда¹ ¹диний
елемент y 2 B, який називають образом елемента |
x 2 A. |
|
Отже, функцiональна вiдповiднiсть, якщо |
A B i äëÿ |
|
будь-якого x 2 A iсну¹ ¹диний елемент |
y 2 B такий, що (x; y) 2 , |
|
тобто будь-якi рiзнi пари, що утворюють |
, мають рiзнi першi коор- |
|
динати. |
|
|
Ï ð è ê ë à ä 5. ßêùî A = f1; 2g i B = f3; 4g, то вiдповiдностi |
||
1 = f(1; 3); (2; 3)g; 2 = f(1; 4); (2; 4)g, |
3 = f(1; 3); (2; 4)g òà 4 = |
|
f(1; 4); (2; 3)g ¹ функцiональними, а будь-яка iнша вiдповiднiсть мiж множинами A i B не ¹ функцiональною (впевнитися в цьому).
Введенi вище поняття декартового добутку множин, вiдповiдностi та функцiонально¨ вiдповiдностi мiж множинами можна проiлюструвати графiчно.
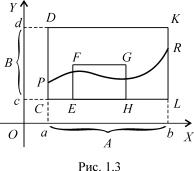
Нехай A=fx : x 2 [a; b] Rg; B = fy : y 2 [c; d] Rg.
Тодi прямокутник CDKL áó-
де зображати декартiв добуток A B (äèâ. ðèñ. 1.3); áóäü-ÿêà
фiгура, яка мiститься в прямокутнику
CDKL, наприклад EF GH, зображатиме вiдповiднiсть мiж A
i B, а будь-яка крива P R, яка ма¹ властивостi:
1) проекцiя P R íà âiñü OX çáiãà¹òüñÿ ç A;
2) будь-яка пряма, проведена паралельно осi OY , перетина¹ P R не бiльше нiж в однiй точцi, зображатиме функцiональну вiдповiднiсть мiж множинами A i B.
1.2.5. Вiдображення та функцiя
З поняттям функцiонально¨ вiдповiдностi тiсно пов'язане поняття
вiдображення àáî функцi¨.
Якщо задано функцiональну вiдповiднiсть мiж множинами A i B, òî вiдображенням f множини A â B àáî функцi¹ю f з множини A â B називають трiйку (A; B; ), яку позначають f : A ! B, àáî
f
A!B, або записують y = f(x); x 2 A; y 2 B.
При цьому A називають множиною (областю) визначення функцi¨ f i позначають D(f); називають ãðàôiêîì f; елемент y 2 B, який ¹ образом елемента x 2 A, називають також значенням вiдображення

1.2. Поняття вiдповiдностi, вiдображення, функцi¨ |
15 |
(функцi¨) f â òî÷öi x i позначають f(x), а множину ff(x) : x 2 D(f)g
називають множиною значень функцi¨ f i позначають E(f). Зрозумiло, що кожне вiдображення f : A ! B цiлком визнача¹-
òüñÿ ñâî¨ì ãðàôiêîì àáî âiäïîâiäíiñòþ
Тому досить часто поняття функцi¨ та функцiонально¨ вiдповiдностi ототожнюють i називають функцi¹ю таку вiдповiднiсть (залежнiсть) мiж двома множинами (змiнними), коли кожному елементу (значенню) однi¹¨ множини (змiнно¨) вiдповiда¹ ¹диний елемент
(¹дине значення) iншо¨ множини (змiнно¨) .
На цьому грунту¹ться графiчний спосiб задання функцi¨ (вiдображення), при якому функцiю f задають ¨¨ графiком (f).
Зрозумiло, що функцiю (вiдображення) f : A ! B можна вважати заданою, якщо для кожного x 2 A вказано його образ f(x) або спосiб (правило) вiдшукання цього образу. Саме тому функцiю f : A ! B часто позначають y = f(x); x 2 A; y 2 B або просто y = f(x).
З цим пов'язаний табличний спосiб задання функцi¨ , при якому функцiя f зада¹ться таблицею, в якiй вказано всi можливi елементи
x 2 A та вiдповiднi ¨м елементи |
y = f(x) 2 B: |
|
|
|
|||||||||
|
x |
|
x1 |
|
x2 |
|
x3 |
|
: : : |
|
xn |
|
: : : |
|
|
|
|
|
|
|
|||||||
|
y = f(x) |
|
y1 |
|
y2 |
|
y3 |
|
: : : |
|
yn |
|
: : : |
Найпоширенiшим способом задання функцi¨ f ¹ аналiтичний спо-
ñiá, при якому за допомогою однi¹¨ або декiлькох формул вказу¹ться правило вiдшукання образу f(x) кожного елемента x 2 D(f).
Якщо функцiю задано аналiтично i область ¨¨ визначення не вказано, то вважають, що вона склада¹ться з усiх точок x, при яких заданi формули мають змiст.
Зауважимо, що будь-яка змiна областi визначення функцi¨ при збереженнi правила вiдшукання образу приводить до виникнення ново¨ функцi¨, яка ма¹ вже сво¨ властивостi.
П р и к л а д 6. Функцiя f(x) = x2 з областю визначення [1 ; 2) ма¹ найменше значення, але не ма¹ найбiльшого. Змiнивши область визначення, включивши до не¨ лише одну точку x = 2 (при збереженнi закону вiдповiдностi), дiстанемо якiсно нову функцiю, яка на вiдрiзку [1; 2] матиме як найменше, так i найбiльше значення.
Елементи множини D(f) можуть позначатися не лише буквою x, але й якими завгодно символами. Це саме стосу¹ться елементiв множини E(f) та само¨ функцi¨.
Здебiльшого в математичному аналiзi розглядають так званi чи- словi функцi¨, тобто такi, у яких множина значень E(f) ¹ числовою,
зокрема функцi¨ дiйсно¨ змiнно¨, êîëè D(f) R i E(f) R. Розглянемо деякi приклади функцiй.
16 Роздiл 1. Елементарнi факти теорi¨ множин
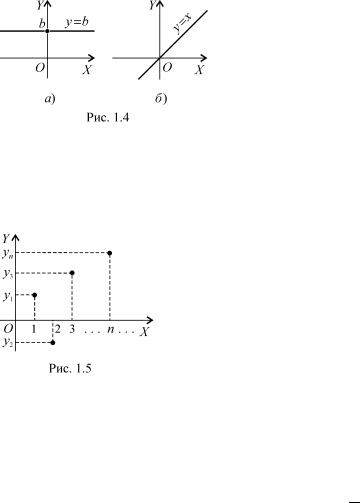
Ï ð è ê ë à ä 7. 1) ßêùî A i B довiльнi непорожнi множини, то рiвнiсть f(x) = b (àáî y = b) 8x 2 A, äå b фiксований елемент з B, визнача¹ сталу функцiю (стале вiдображення) f : A ! B.
Зокрема, якщо A = B = R1, òî ãðàôiê (f) стало¨ фун-
кцi¨ можна уявляти як пряму, зображену на рис. 1.4, a).
2) ßêùî A = B 6= ?, òî ðiâíiñòü f(x) = x (àáî y =
x) 8x 2 A визнача¹ òîòî-
жнe вiдображення (тотожну
функцiю).
Це вiдображення зберiга¹ будь-який елемент x 2 A, коли вiд нього перейти до його образу.
ßêùî A = B = R1, òî ãðàôiê (f) тотожного вiдображення мо-
жна уявляти як пряму, зображену на рис. 1.4, б ) (бiсектриса першого й третього координатних кутiв).
3) ßêùî A = N, à B 6= ?, òî ðiâíiñòü f(n) = y = yn 2 B 8n 2 N визнача¹ функцiю, яку називають ïîñëiäîâíiñòþ.
Отже, послiдовнiсть це будь-яка функцiя f, визначена на множинi на-
туральних чисел.
При цьому образ натурального чи- сла n, тобто f(n), позначають yn i íà-
зивають n-м або загальним членом послiдовностi, а саму послiдовнiсть позна- чають f = (yn).
Зокрема, якщо значеннями послiдовностi ¹ числа, то ¨¨ називають числовою. Графiк числово¨ послiдовностi з дiйсни-
ми членами можна зобразити у виглядi множини окремих точок площини OXY (ðèñ. 1.5).
4) ßêùî n 2 Z фiксоване число, то рiвнiсть f(x) = xn визнача¹
степеневу функцiю з цiлим показником .
Область визначення та властивостi цi¹¨ функцi¨, зокрема вигляд
графiка залежать вiд показника |
n. |
|
:= ( px) |
|
|||
5) Ðiâíiñòü f(x) = x n |
:= (xn ) |
|
|
||||
m |
|
1 |
m |
n |
|
|
m визнача¹ степеневу |
функцiю з довiльним фiксованим рацiональним показником mn Âëà- стивостi таких функцiй та вигляд ¨х графiкiв залежить вiд показника
m=n.
1.2. Поняття вiдповiдностi, вiдображення, функцi¨ |
17 |
|
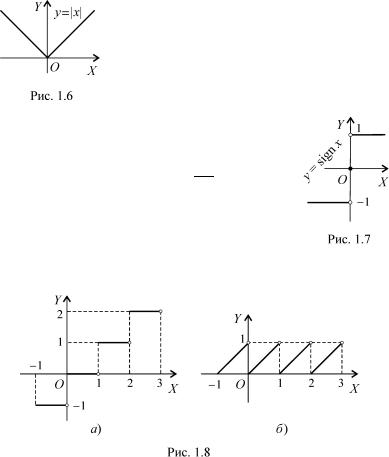
6) Ðiâíiñòü y = f(x) = |
x; êîëè x < 0; |
|
|
|
x; êîëè x > 0; |
визнача¹ функцiю модуль x (позначають jxj ), |
||
7) Ðiâíiñòü y = f(x) = |
8 |
0; êîëè x = 0; |
ðèñ. 1.6. |
< |
1; êîëè x > 0; |
|
||
|
1; êîëè x < 0; |
|
визнача¹ функцiю, яка носить назву ñiãíóì x |
: |
|
àáî çíàê x (позначають sign x), ðèñ. 1.7.
8) Якщо A = f1; 2; : : : ; ng для деякого n 2 N, а B 6= ?, то рiвнiсть
y = f(k) =: yk 2 B 8k 2 1; n
визнача¹ функцiю, яку називають скiнченíîþ послiдовнiстю i позначають f = (fk); k 2 1; n.
9) Ðiâíiñòü y = [x] визнача¹ функцiю, яку
називають цiлою частиною дiйсного числа , [x]
найбiльше цiле число, що не перевищу¹ зна- чення x (¨¨ графiк зображено на рис. 1.8, а)).
10) Функцiю y = x [x] називають дробовою частиною дiйсного числа x; ¨¨ позначають fxg. Графiк цi¹¨ функцi¨ зображено на рис. 1.8, б ).
1.2.6. Вза¹мно однозначнe вiдображення
Якщо заданo вiдображення f : A ! B i A1 A, то множину образiв всiх елементiв множини A1 позначають f(A1), тобто
f(A1) = fy 2 B : (9 x 2 A1 : f(x) = y)g:
При цьому f(A1) називають образом множини A1. Зокрема, множиною значень вiдображення f : A ! B ¹ множина E(f) = f(A).
Взагалi кажучи, для вiдображення f : A ! B множина значень
E(f) 6= B.
18 |
Роздiл 1. Елементарнi факти теорi¨ множин |
Ï ð è ê ë à ä 8. Âiäïîâiäíiñòü Ã(f) = f(1; 3); (2; 3)g зада¹ вiдображення f : f1; 2g ! f3; 4g, для якого E(f) = f3g 6= f3; 4g.
ßêùî æ E(f) = B, то вiдображення f : A ! B називають вiдображенням множини A на B.
Ï ð è ê ë à ä 9. ßêùî f : f1; 2g ! f3; 4g, òî f вiдображення множини f1; 2g íà f3; 4g òîäi é òiëüêè òîäi, êîëè Ã(f) = f(1; 3); (2; 4)g àáî Ã(f) = f(1; 4); (2; 3)g.
Серед усiх вiдображень множини A íà B видiляють âçà¹ìíî îäíî-
значнi вiдображення, тобто такi вiдображення f : AíàB, äëÿ ÿêèõ
!
f(A) = B i рiзнi елементи множини A мають рiзнi образи. При цьому записують f : A $ B, àáî A f! B, àáî y â.î.f(x); x 2 A; y 2 B.
=
П р и к л а д 10. Кожне вiдображення множини f1; 2g íà f3; 4g ¹ вза¹мно однозначним, а кожне вiдображення f1; 2; 3g íà f1; 2g не ¹ вза¹мно однозначним.
Нехай задано множини Xk; k 2 N. Розглянемо множину P усiх послiдовностей (xk) та множини Pn; n 2 N усiх скiнченних послiдов-
ностей (xk); k 2 1; n, äå xk 2 Xk 8k 2 N. (xk) = (yk) , xk = yk 8k. Якщо iсну¹ вiдображення f : P $ A (f : Pn $ A при деякому n 2 N), то казатимемо, що елементи множини A цiлком визнача-
ються нескiнченною (скiнченною) кiлькiстю iндексiв xk 2 Xk; k 2
N (k 2 1; n) i записуватимемо A = fax1;x2;:::;xn;::: : xk 2 Xk 8k 2
Ng (A = fax1;x2;:::;xn : xk 2 Xk 8k 2 1; ng). Множину A називатимемо при цьому iндексованою множиною, а елементи xk 2 Xk iндексами
елементiв множини A.
1.2.7. Обернене вiдображення, oбернена функцiя
Кожне вза¹мно однозначне вiдображення |
f : A $ B ì๠обернене |
вiдображення f 1 : B $ A, тобто таке, що |
f 1(y) = x , x 2 A i |
f(x) = y 8y 2 B. |
x = f 1(y); y 2 B; x 2 |
Обернене вiдображення позначають також |
A i називають оберненою функцi¹ю до функцi¨ f, а саму функцiю f у цьому випадку називають оборотною.
Для вiдшукання функцi¨, обернено¨ до y = f(x); x 2 A, достатньо розв'язати вiдносно невiдомого x рiвняння f(x) = y, вважаючи y 2
B = E(f) фiксованим. Якщо для всiх y 2 B такий розв'язок iсну¹ i ¹диний, то вiн i визнача¹ шукану обернену функцiю x = f 1(y); y 2 B.
Âiншому разi вiдповiдна обернена функцiя не iсну¹.
Ïр и к л а д 11. 1) Лiнiйна функцiя y = kx + b ¹ оборотною,
êîëè k 6= 0, i оберненою до не¨ ¹ функцiя x = k1 y kb
2) Квадратична функцiя y = x2 не ¹ оборотною, оскiльки рiвняння y = x2 вiдносно дiйсного невiдомого x ì๠äâà ðîçâ'ÿçêè x = py.
1.2. Поняття вiдповiдностi, вiдображення, функцi¨ |
19 |
Проте, коли розглядати функцiю y = x2; x 2 [0; +1), тобто |
D(f) = |
[0; +1), то вона вже ¹ оборотною, i оберненою до не¨ ¹ функцiя x = py. Так само функцiя x = py ¹ оберненою до функцi¨ y = x2,
x 2 ( 1; 0).
Точки M(x; y) i M0(y; x) ¹ симетрични-
ми вiдносно прямо¨ y = x, îñêiëüêè öÿ ïðÿ-
ма ¹ серединним перпендикуляром до вiдрiзка MM0.
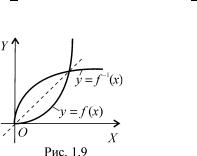
Òîìó ãðàôiêè Ã(f) = f(x; f(x)) : x 2 Ag i Ã(f 1) = f(y; f 1(y)) = (f(x); x) : x 2 Ag
¹ симетричними вiдносно прямо¨ y = x, Отже, якщо функцiю x = f 1(y), îáåð-
нену до функцi¨ y = f(x), записати у виглядi y = f 1(x) (що, до речi, й роблять для
зручностi), то ¨¨ графiк стане симетричним до графiка функцi¨ f вiдносно прямо¨ y = x (ðèñ.1.9).
П р и к л а д 12. Якщо для вiдображення f : |
f1; 2g $ f3; 4g |
éîãî ãðàôiêîì ¹ Ã(f) = f(1; 3); (2; 4)g, то вiдображення |
f 1 : f3; 4g $ |
f1; 2g ì๠ãðàôiê Ã(f 1) = f(3; 1), (4; 2)g. |
|
Коли вiдображення f : A ! B не ¹ вза¹мно однозначним, то вва-
жають, що воно не ма¹ оберненого вiдображення (функцiя f не ма¹ обернено¨) у розумiннi даного вище означення вiдображення (функцi¨). Функцiю f при цьому називають необоротною.
П р и к л а д 13. Будь-яке вiдображення f : f3; 4; 5g ! f1; 2g не ма¹ оберненого вiдображення; функцiя f(x) = sin x, визначена на
множинi R, не ма¹ обернено¨ функцi¨.
1.2.8. Композицiя (суперпозицiя) функцiй, або складна функцiя
Нехай задано функцi¨ f : A ! B i ' : E ! A. Òîäi композицi¹ю f ' цих функцiй називають функцiю, значення яко¨ знаходять за формулою f '(x) = f('(x)); 8x 2 E. Функцiю f ' називають також
складною функцi¹ю, àáî суперпозицi¹ю функцiй f та '. При цьому ' називають внутрiшньою, à f зовнiшньою функцi¹ю.
Ï ð è ê ë à ä 14. |
1 |
|
|
|
f ' |
|
|
f |
|
' |
|
|
Cуперпозицi¹ю |
|
функцiй |
|
i |
|
äiéñíî¨ |
||||
çìiííî¨, äëÿ ÿêèõ f(x) = x2 ; '(x) = x2, |
¹ функцiя |
, значення яко¨ |
|||||||||
|
2 |
) |
1 |
= jxj 8x 2 R |
|
|
' f(x) = |
||||
знаходять за формулою |
2 |
, à |
|||||||||
1 |
(x) = (x |
|
|
|
|||||||
(x2 )2 = x 8x>0. |
|
|
|
|
|
|
|
|
|
|
|
Iз наведеного вище означення виплива¹, що композицiя (суперпо-
зицiя) функцiй f òà ' iñíó¹ òîäi é òiëüêè òîäi, êîëè |
E(') D(f). |
П р и к л а д 15. Iсну¹ суперпозицiя функцiй |
f ', äå f(x) = |
sin x; x 2 R, à '(x) = ln x; x 2 (0; +1), проте не iсну¹ суперпозицi¨

20 |
Ðîçäië 1. |
Елементарнi факти теорi¨ множин |
' f цих функцiй. |
|
|
1.2.9. Тотожнi функцi¨ |
|
|
|
Двi функцi¨ (вiдображення) |
f i ' називають рiвними àáî òîòî- |
жними, ÿêùî D(f) = D(') i f(x) = '(x) 8x 2 D(f). При цьому записують f = '.
Ï ð |
è |
к л а д 16. Функцi¨ f òà ', визначенi формулами |
f(x) = jxj |
i |
'(x) = x ¹ тотожними, якщо покласти D(f) = D(') = |
[0; +1). Однак, якщо вважати, що D(f) = D(') = R, òî f i ' âæå
не ¹ тотожними функцiями.
1.2.10. Числовi функцi¨
У класичному математичному аналiзi найчастiше мають справу з функцiями f : A ! B, якi, залежно вiд того, якому простору нале-
жать множини D(f) i E(f) мають спецiальну назву (див. таблицю).
1) Функцi¨ однi¹¨ дiйсно¨ змiнно¨ , тобто такi, що
D(f) R i E(f) R;
¨х найчастiше позначають y = f(x); x 2 A; y 2 B;
2) функцiями комплексно¨ змiнно¨ , тобто такими, що
D(f) C i E(f) C;
¨х позначають w = f(z); z 2 A; w 2 B;
3) функцi¨ кiлькох змiнних, тобто такi, що
D(f) Rn i E(f) R;
¨х позначають
u = f(x1; x2; : : : ; xn); (x1; x2; : : : ; xn) 2 A; u 2 R:
Зокрема, при n = 2 ìà¹ìî функцiю двох змiнних u = f(x; y); (x; y) 2 D(f); u 2 R;
à ïðè n = 3 функцiю трьох змiнних
u = f(x; y; z); (x; y; z) 2 D(f); u 2 R:
Графiком функцi¨ двох змiнних часто ¹ деяка поверхня у просторi OXY Z.
Кожна з названих у таблицi функцiй вiдноситься до числових функцiй, тобто до функцiй, значеннями яких ¹ числа (дiйснi або комплекснi).
Над числовими функцiями можна виконувати арифметичнi операцi¨, вважаючи за означенням, що сума f +', рiзниця f ', добуток f '
