
ifmion_kma_Mykhalin_Dujenkova(Mnozhyny)
.pdf2.4. Множини Q рацiональних та R дiйсних чисел |
91 |
Десятковi дроби були вiдомi вже в ХIУ ХУ сторiччi. Арабський маьтематик аль-Кашi описав ¨х у 1427 р. В вропi десятковi дроби ввiв нiдерландський вчений С.Стевiн (1548 1620).
2.4.12. Зв'язок iз шкiльним курсом математики
У шкiльному курсi математики досить детально вивчаються рацiональнi числа, чого не можна сказати про дiйснi числа. Викладенi у цьому параграфi факти про дiйснi числа показують, чому в курсi математики загальноосвiтньо¨ школи можна лише продекларувати деякi вiдомостi про дiйснi числа. У класах з поглибленим вивченням математики цi вiдомостi можна значно розширити та поглибити. Тому вчи- тель математики повинен володiти теорi¹ю дiйсних чисел принаймнi на викладеному рiвнi.
2.4.13. Постановка проблем
У процесi вивчення властивостей дiйсних чисел, грунтуючись на ¨хнiх визначальних властивостях, прийшли до проблеми визначення дiйсних за допомогою нескiнченних десяткових дробiв. Цю проблему до кiнця ще не розв'язано. Було показано, що на точки прямо¨ можна дивитися у певному розумiннi як на дiйснi числа. Виника¹ питання, чи не можна розглядати точки площини теж як деякi числа, якi мiстять серед себе дiйснi числа.
2.4.14. Контрольнi запитання та завдання
1. |
Перевiрити, чи правильними ¹ такi твердження: |
|||||||||
1) |
ÿêùî c 2 Q, то iснують такi числа |
m; n 2 N, ùî c = |
m |
|||||||
n |
; |
|||||||||
2) |
твердження, обернене до 1), ¹ правильним; |
|||||||||
3) рацiональнi числа c = |
m |
|
c = |
p |
|
|
|
|
||
n i |
q |
ðiâíi òîäi é òiëüêè òîäi, êîëè |
||||||||
|
|
|
||||||||
m = p i n = q;
4)множина Q рацiональних чисел задовольня¹ властивостi I IУ дiйсних чисел;
5)(a; b) \ Q 6= ? 8a; b 2 R;
6)ÿêùî c скiнченний десятковий дрiб, то c 2 Q;
7)твердження, обернене до 6), ¹ правильним;
8) якщо множина E Q i E обмежена зверху, то sup E 2 Q;
9)кожне дiйсне число ¹ рацiональним або iррацiональним;
10)кожне iррацiональне число ¹ нескiнченним десятковим дробом.
2. Довести данi твердження:
1)не кожний нескiнченний десятковий дрiб ¹ iррацiональним чи-
ñëîì;
2)ÿêùî a 2 Q, то воно ¹ нескiнченним перiодичним дробом;

92 |
|
|
|
|
|
|
|
Ðîçäië 2. |
|
Множини дiйсних i комплексних чисел |
||||||||||||||
3) |
|
[nx] |
6 x < |
|
[nx] |
1 |
|
|
8x 2 R; |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|||||||
|
n |
|
|
|
|
|
n |
n |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 + x2 + |
+ xn |
|
|
|
|
|
|||||
4) |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
px1x2 |
: : : xn 6 |
|
|
|
|
|
n |
|
8xk > 0 (íåðiâíiñòü Êîøi); |
|||||||||||||
5) (1 + |
1 |
)n < (1 + |
|
1 |
|
|
)n+1; |
6) n! < ( |
n + 1 |
)n. |
||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
n + 1 |
|
|
|
2 |
|
|
|||||
У нерiвностях 3) 6) n 2 N. |
|
|
|
|
|
|
||||||||||||||||||
3. |
Нехай степiнü з довiльним дробовим показником визнача¹ться |
|||||||||||||||||||||||
|
|
|
|
|
|
m |
|
n |
m, äå |
|
|
|
|
|
|
m |
||||||||
ðiâíiñòþ |
a |
n |
= ( |
p |
a) |
|
|
|
|
n 2 N; m 2 Z |
i äðiá |
|
|
|||||||||||
|
|
|
|
n нескоротний (за |
||||||||||||||||||||
умови iснування право¨ частини рiвностi). Показати, що цей степiнь ма¹ властивостi:
|
|
m |
|
|
|
m |
m |
|
a |
m |
a m=n |
|
||||||||
1) |
(ab) n = a n b n |
òà ( |
|
) n = |
|
|
|
|
||||||||||||
b |
b m=n , коли iснують правi частини; |
|||||||||||||||||||
|
m |
|
p |
m p |
|
|
m |
p |
|
a |
m=n |
|
||||||||
2) a n |
+ q = a n a q òà a n |
q = |
|
|
|
|
||||||||||||||
b p=q , коли iснують правi части- |
||||||||||||||||||||
íè; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
m |
p |
|
|
|
mp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
(a n ) q |
|
= a nq , êîëè a > 0. Чи правильна ця рiвнiсть для a < 0?; |
|||||||||||||||||
4) |
ÿêùî |
|
m |
|
p |
|
m |
p |
|
|
|
|
m |
p |
||||||
|
< |
|
a n |
< a q |
, êîëè a > 1, i a n |
> a q , êîëè |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
n |
|
q , |
òî |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 < a < 1;
11
5)an < bn , êîëè a < b i n = 2k 1 àáî 0 < a < b i n = 2k.
2.5. Комплекснi числа
У п. 2.4.12 поставлено питання про можливiсть розглядати точки площини як деякi числа, частинним випадком яких ¹ дiйснi числа. Позитивну вiдповiдь на це питання дано в цьому параграфi завдяки введенню множини комплексних чисел.
Розглянуто рiзнi форми запису та зображення комплексних чисел, властивостi модуля й аргументу, арифметичнi операцi¨ та добування кореня, а також доведено важливу формулу бiнома Ньютона для довiльних комплексних чисел.
2.5.1. Поняття комплексного числа i множини C
Якщо у площинi XOY (див. рис. 2.7) вибрати декартову прямокутну систему координат, то кожну точку (x; y) цi¹¨ площини можна ототожнити з виразом x + iy, який назвемо комплексним числом i позначимо z = x + iy.
При цьому число x називають дiйсною частиною комплексного числа z i позначають Re z, а число y називають уявною частиною

2.5. Комплекснi числа |
|
93 |
|
z i позначають |
Im z, à i |
називають уявною одиницею, вважаючи, що |
|
i2 = 1. |
|
ßêùî y = Im z = 0, то замiсть позначення |
|
|
|
||
|
z = x + i0 пишуть z = x, завдяки чому кожне |
||
|
дiйсне число ¹ комплексним, у якого уявна ча- |
||
|
стина дорiвню¹ нулю. |
||
|
|
ßêùî y |
= Im z 6= 0, то комплексне число |
|
z = x + iy |
називають уявним числом, à ÿêùî, |
|
|
êðiì òîãî, x = Re z = 0, òî z = iy називають |
||
|
суто уявним числом. |
||
|
|
Множину всiх комплексних чисел познача- |
|
ють буквою C, |
а площину XOY , точки (x; y) яко¨ ототожнюють |
||
з комплексними числами |
x + iy, називають комплексною площиною. |
||
Oскiльки точки |
(x; 0) ототожнюють з дiйсними числами x, òî âiñü |
||
OX називають дiйсною вiссю, à âiñü OY , точки яко¨ (0; y) (крiм точки
(0; 0)) ототожнюють з суто уявними числами |
|
iy, називають уявною |
||||||||
âiññþ. Точку (0; 0) ототожнюють з нулем: 0 = 0 + i0. |
|
|
||||||||
Точку (x; y) |
координатно¨ площини можна розглядати як вектор |
|||||||||
|
~ |
|
~ |
. Поклавши в цьому розкладi |
1 |
çàìiñòü ~ òà |
i |
çàìiñòü |
||
(x; y) = x i+y j |
|
|
|
i |
|
|||||
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
~, дiстанемо |
(x; y) = x + y i = x + iy = z |
. |
|
|
|
|
||||
j |
|
! |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Отже, комплекснi числа можна розглядати як вектори площини |
||||||||||
XOY (äèâ. ðèñ. 2.7). |
|
|
|
|
|
|
||||
Два комплекснi числа z1 = x1 + iy1 i z2 |
= x2 + iy2 |
природно |
||||||||
вважати рiвними òîäi é òiëüêè òîäi, êîëè x1 = x2 i y1 = y2. Зокрема, |
||||||||||
z = 0 , Re z = 0 i Im z = 0, а число z = 0 називають нулем множини C комплексних чисел.
2.5.2. Модуль, аргумент i тригонометрична фор- |
||||||||
ма комплексного числа |
|
|
|
|
|
|
|
|
Оскiльки кожне комплексне число |
z = x+iy можна ототожнювати |
|||||||
з вектором, який ма¹ початок у точцi |
(0; 0) |
i êiíåöü ó òî÷öi (x; y), òî |
||||||
замiсть слiв "комплексне число z = x + iy" часто вживають слова |
||||||||
|
|
|
|
|
|
|
|
|
"вектор z = x + iy". Довжину цього вектора |
px |
2 |
+ y |
2 позначають |
jzj |
|||
i називають модулем комплексного числа z. |
|
|
|
|||||
Êóò ', утворений вектором ~z з додатним на- |
||||||||
прямом дiйсно¨ осi, називають аргументом z. |
|
|||||||
Зрозумiло, що кожне комплексне число ма¹ ¹ди- |
||||||||
ний модуль, а якщо z 6= 0, то iсну¹ i аргумент |
z, |
|||||||
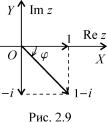
але вiн не ¹диний. Множину всiх значень аргументу z позначають Arg z, а те його значення, що лежить
ó ïðîìiæêó ( ; ], називають головним значенням аргументу i позначають arg z (äèâ. ðèñ. 2.8).
Неважко помiтити, що Arg z = farg z + 2k :
94
k 2
Роздiл 2. Множини дiйсних i комплексних чисел
Zg: Часто останню рiвнiсть записують у виглядi
Arg z = arg z + 2k ; k 2 Z:
Вважають, що число z = 0 не ма¹ аргументу.
З геометричних мiркувань (див. рис. 2.9) виплива¹, що 8z 6= 0
z = jzj(cos ' + i sin ') = jzj(cos arg z + i sin arg z) = |
(1) |
= jzj(cos Arg z + i sin Arg z); |
|
розумiючи пiд Arg z довiльне фiксоване значення аргументу даного z. Рiвнiсть (1) називають тригонометричною формою комплексного
числа z, тодi як запис |
|
z = x + iy |
|
¹ éîãî алгебра¨чною формою. |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
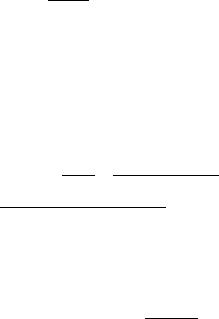
П р и к л а д 1. Запишемо у тригономе- |
|||||||||||||||||||||
тричнiй формi комплексне число |
z = 1 i. |
|
||||||||||||||||||||||
|
|
|
Визнача¹мо модуль |
|
|
p |
|
|
|
p |
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
i áó- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jzj = 1 + 1 = |
|
|||||||||
ду¹мо вектор |
|
z (ðèñ. 2.9). |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
З геометричних мiркувань дiста¹мо |
|
|
|
||||||||||||||||||
|
|
|
' = arg z = |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Òîìó |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 i = |
|
|
2(cos( |
|
) + i sin( |
|
): |
|
||||||||||
|
|
|
|
|
|
|
|
4 |
4 |
|
||||||||||||||
|
|
|
Для обчислення arg z |
можна скористатись |
||||||||||||||||||||
такими формулами: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
8 |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
arctg |
y |
; |
|
|
x > 0; |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
arg z = |
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
> |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
> |
|
|
|
|
|
|
; |
x < 0; y < 0; |
|
|
|
|
|
|
|
||||||||
|
> arctg |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
> arctg |
|
+ ; |
x < 0; y > 0; |
|
|
|
|
|
|
|
|||||||||||||
|
< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
2 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
> |
|
signxy; |
|
x = 0; y = 0; |
|
|
|
|
|
|
|
||||||||||||
2.5.3.Арифметичнi операцi¨ над комплексними числами
Враховуючи, що комплекснi числа це вектори, природно арифметичнi операцi¨ над ним ввести так: сума z1 + z2 комплексних чисел z1
i z2 це число
z1 + z2 = (x1 + iy1) + (x2 + iy2) := (x1 + x2) + i(y1 + y2);
добуток z1 z2 комплексних чисел z1 i z2 це число
z1 z2 = (x1 + iy1) (x2 + iy2) = (x1x2 y1y2) + i(x1y2 + x2y1);
2.5. Комплекснi числа |
95 |
де враховано, що i2 = 1.
Неважко помiтити, що сума й добуток комплексних чисел задовольняють властивостi I II дiйсних чисел (див. п. 2.1.1). Пропону¹мо читачевi впевнитися в цьому самостiйно.
Зауважимо тiльки, що одиницею в C ¹ число z = 1 = 1 + i0, протилежним елементом для z = x+iy ¹ число ( z) = x iy, а оберненим
äëÿ z = 0 ¹ число z 1 = |
x iy |
= |
1 |
|
|
|
|||||||||||||||
z |
|
|
|||||||||||||||||||
6 |
|
|
|
|
|
|
x2 + y2 |
|
|
||||||||||||
Поняття рiзницi та частки комплексних чисел вводяться так само, |
|||||||||||||||||||||
як i для дiйсних чисел. |
|
|
|
|
|
|
|
|
|
|
kQ |
|
|
||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
Так само як i для дiйсних чисел вводяться вирази |
zk добуток |
||||||||||||||||||||
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
=1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
чисел zk; k 2 |
1; n, òà |
k=1 zk сума чисел zk; k 2 1; n. |
|
|
|||||||||||||||||
Комплексне число |
z = x |
|
iy називають спряженим до компле- |
||||||||||||||||||
|
|||||||||||||||||||||
ксного числа |
z = x + iy. Неважко помiтити, що |
z z = jzj2 |
, |
||||||||||||||||||
z1 z2 = (x1 + iy1) (x2 + iy2) = (x1 x2) + i(y1 y2); |
|||||||||||||||||||||
|
z1 |
= |
x1 + iy1 |
= |
z1 z2 |
= |
(x1 + iy1)(x2 iy2) |
= |
|
||||||||||||
|
|
|
|
||||||||||||||||||
|
z2 |
|
|
x2 + iy2 |
|
z2 z2 |
|
x22 + y22 |
|
|
|||||||||||
|
|
|
= |
(x1x2 + y1y2) + i(x2y1 x1y2) |
; z2 = 0; |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
x22 + y22 |
|
6 |
|
|
|
|||||||
тобто з комплексними числами оперують, як iз многочленами: розкри-
вають дужки та зводять подiбнi члени, вважаючи, що i i = i2 = 1:
Ï ð è ê ë à ä 2. ßêùî |
z1 |
, |
|
|
|
|
òî |
z1 + z2 = (1 |
+ i) + |
||||||||
|
|
|
|
|
|
|
|
= 1 + i z2 = 1 i; |
|
2 |
= 2; |
||||||
(1 i) = 2, z1 z2 = (1+i) (1 i) = 2i, z1 z2 = (1+i)(1 i) = 1 i |
|
||||||||||||||||
|
z1 |
= |
1 |
+ i |
= |
(1 + i)(1 + i) |
|
= |
1 + |
2i 1 |
= i: |
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||||
|
z2 |
|
i |
|
|
|
|
||||||||||
|
1 |
(1 i)(1 + i) |
1 |
+ 1 |
|
|
|
||||||||||
2.5.4. Основнi властивостi модуля i аргументу
Вiдмiтимо деякi важливi властивостi модуля та аргументу комплексного числа.
Властивiсть 1 (к р и т е р i й р i в н о с т i к о м п л е к с н и х ч ис е л).
ßêùî z1 6= 0 i z2 6= 0, òî z1 = z2 |
, |
|
jz1j = jz2j i Arg z1 = Arg z2. |
|||||||
Властивiсть 2 |
(ï î ð i â í ÿ í í ÿ |
jzj |
ç jRe zj i jIm zj): |
|
|
|
||||
jzj > jRe zj i jzj > jIm zj, àëå jzj 6 jRe zj + jIm zj. |
|
|
|
|
||||||
Властивiсть 3 |
(ì î ä ó ë ü ñ ó ì è, ð i ç í è ö i, ä î á ó ò ê ó é |
|
|
|||||||
÷ à ñ ò ê è): |
|
|
|
|
|
|
= jjz2jj. |
|||
jjz1j jz2jj 6 jz1 z2j 6 jz1j + jz2j, jz1 z2j = jz1j jz2j i z2 |
||||||||||
|
(à ð ã ó ì å í ò ä î á ó ò ê ó é ÷ à ñ ò ê è): |
z1 |
|
z1 |
||||||
Властивiсть 4 |
|
|
|
|||||||
|
|
|
z1 |
|
|
|
|
|
||
Arg (z1 z2) = Arg z1 + Arg z2, a Arg |
= Arg z1 Arg z2; z1; z2 6= 0. |
|||||||||
z2 |
|
|||||||||

96 Роздiл 2. Множини дiйсних i комплексних чисел
Ç à ó â à æ å í í ÿ. Ðiâíiñòü Arg z1 = Arg z2 розумiють як рiвнiсть двох множин. Аналогiчно розумiють i рiвностi з властивостi 4.
Проiлюстру¹мо можливi методи доведення цих властивостей. Зрозумiло, що
p
jz1 z2j 6 jz1j + jz2j , (x1 x2)2 + (y1 y2)2 6
6x21 + y12 + x22 + y22 , x21 + x22 + y12 + y22 2(x1x2 + y1y2) 6
q q
6 x21 + x22 + y12 + y22 2 x21 + y12 x22 + y22 ,
q q
, (x1x2 + y1y2) 6 x21 + y12 x22 + y22:
Якщо лiва частина останньо¨ нерiвностi ¹ вiд'¹мною, то нерiвнiсть правильна. А коли лiва частина нерiвностi невiд'мна, то вона рiвносильна такiй нерiвностi
(x1x2 + y1y2)2 6 (x21 + y12)(x22 + y22) ,
, x21 x22 + y12 y22 + 2x1 x2 y1 y2 6 x21 x22 + y12 y22 + x1y22 + y22x22 , , 2x1 x2 y1 y2 6 x21y22 + x22y12 , (x1y2 y1x2)2 > 0;
i знову дiста¹мо правильну нерiвнiсть. Тому правильною ¹ нерiвнiсть про модуль суми та рiзницi: jz1 z2j 6 jz1j + jz2j.
Iншi нерiвностi пропону¹мо читачевi довести самостiйно.
Для доведення властивостi 4 розглянемо комплекснi числа z1 i z2, записанi в тригонометричнiй формi. Тодi матимемо:
z1 z2 = jz1j(cos Arg z1 + i sin Arg z2) jz2j(cos Arg z2 + i sin Arg z2) =
jz1jjz2j((cos Arg z1 cos Arg z2 sin Arg z1 sin Arg z2)+ +i(cos Arg z1 sin Arg z2 + sin Arg z1 sin Arg z2)) = jz1jjz2j((cos(Arg z1 + Arg z2) + i sin(Arg z1 + Arg z2) ) ) jz1 z2j = jz1j jz2j i Arg(z1 z2) = Arg z1 + Arg z2:
Мiркування для частки пропону¹мо читачевi довести самостiйно.
Використовуючи метод математично¨ iндукцi¨, неважко узагальни-
Qn Pn
ти властивiсть 3, показавши, що Arg |
zk = |
Arg zk |
|
|
|
||||||||
8 n 2 |
n |
6 |
|
k=1 |
k=1 |
|
|
|
|||||
|
zk |
C : zk |
= 0. При цьому дiста¹мо також рiвнiсть |
|
|
|
|||||||
|
kQ |
Q |
|
|
|
|
|
|
n |
n , |
|||
j |
=1 zkj = k=1 jzkj. |
|
|
|
|
|
|
|
|
|
|||
|
Зокрема, якщо zk = z 6= 0 8k |
2 |
1; n |
, |
òî ìà¹ìî |
jz |
|
j = jzj |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Arg zn = nArg z |
i |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
zn = jzjn(cos nArg z + i sin nArg z); |
|
|
(3) |
||||||

2.5. Комплекснi числа |
97 |
Рiвнiсть (3) називають формулою Муавра.
Ï ð è ê ë à ä 3. (1 + i)16 = (p2)16(cos 4 + i sin 4 ) = 28 = 256.
За допомогою формули (3) можна розв'язати рiвняння wn = z вiдносно w äëÿ âñiõ n 2 N.
2.5.5. Êîðiíü n-го степеня з комплексного числа
Коренем n-го степеня з комплексного числа |
z називають таке чи- |
||||
ñëî w, для якого w |
n |
= z. При цьому записують |
w = pz. |
||
|
|
n |
|
|
|
Зрозумiло, що коли z = 0, то ¹диним коренем |
n-го степеня з цього |
||||
числа ¹ число w = 0. |
z 6= 0. Òîäi z = jzj(cos arg z + i sin arg z) i число |
||||
Припустимо, що |
|||||
w = jwj(cos ' + i sin ') ¹ коренем, n-го степеня з числа z òîäi é òiëüêè òîäi, êîëè
wn = z , |
jwjn(cos n' + i sin n') = jzj(cos arg z + i sin arg z) |
, |
|
||||||||||||||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
arg z + 2k |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
, jwj |
|
= jzj |
i n' = arg z + 2k |
, |
jwj = |
+ jzj |
i ' = |
|
|
|
|
|
; |
||||||||||||||||||||||||
|
|
|
n |
|
|||||||||||||||||||||||||||||||||
k 2 Z: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
||
Îòæå, êîëè z 6= 0, то кожне число |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
arg z + 2k |
|
|
|
|
|
arg z + 2k |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w = wk = |
|
z = + jzj (cos |
|
|
|
|
|
|
|
+ i sin |
|
|
|
|
|
); k 2 Z; |
|
||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
n |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
äå n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jzj, ¹ кoренем n-ãî |
||||||||||||||
+ jzj |
|
арифметичний корiнь |
n-го степеня з |
||||||||||||||||||||||||||||||||||
степеня з числа |
|
z |
i навпаки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Неважко помiтити, що серед усiх чисел |
wk iñíó¹ ëèøå n попарно |
||||||||||||||||||||||||||||||||||||
рiзних значень, якi можна дiстати, надаючи |
k значень вiд 0 äî n 1. |
||||||||||||||||||||||||||||||||||||
Таким чином, для вiдшукання усiх коренiв n-го степеня з числа z |
|||||||||||||||||||||||||||||||||||||
можна користуватися формулою: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arg z + 2k |
|
arg z + 2k |
|
|
|
|||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
||||||||||||||||||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
z = wk = jzj (cos |
|
|
n |
|
|
|
+ i sin |
|
n |
|
|
); |
|
|
(4) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 2 |
0; n 1 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
||||||||||||||||||||||||||||||||||||
Легко бачити, що точки |
wk; k 2 |
0; n 1 |
, у комплекснiй площинi ¹ |
||||||||||||||||||||||||||||||||||
вершинами правильного n-кутника, вписаного у коло з центром у точцi 0 i радiусом r = n jzj.
+ |
|
|
|
|
|
i ñàìå éîãî íàé- |
|
головним значенням кореня n-гоpстепеня з числа z |
|||||||
p |
n |
|
|
arg z |
|
arg z |
|
jzj (cos |
|
|
|||||
Зауважимо, що число w0 = |
+ |
n |
+ i sin |
n |
) називають |
||
|
|
|
|
|
|
|
|
p
частiше позначають n z.

98 |
Ðîçäië 2. |
Множини дiйсних i комплексних чисел |
||||||||
|
Ï ð è ê ë à ä 4. 1) ßêùî |
z = x > 0, òî jzj = z = x, arg z = 0, i |
||||||||
за формулою (4) числа |
|
|
|
|
|
|
|
|||
|
p |
|
|
|
|
|
|
|
|
|
|
n |
|
|
2k |
|
2k |
||||
|
wk = + x (cos |
|
|
+ i sin |
|
); k 2 0; n 1; |
||||
|
n |
n |
||||||||
утворюють множину усiх значень кореня n-го степеня з додатного чи-
ñëà z = x. При цьому: p
n x головне значення кореня ¹ дiйсним i збiга¹ться з
+
арифметичним коренем;
á) ÿêùî n = 2m + 1, òî w0 ¹динe дiйснe значення кореня n-го степеня з додатного числа z = x;
â) ÿêùî n = 2m, òî êðiì w0
p
wm = n x (cos
+
а всi iншi значення wk 62R. Отже, серед усiх коренiв z = x дiйсними ¹ лише числа
2) ßêùî z = x < 0, то числа
2m |
|
2m |
p |
|
|
|
|
n |
|
|
|||
|
+ i sin |
|
) = |
|
x; |
|
2m |
2m |
|
||||
n = 2m-го степеня з додатного числа p
n x.
jzj = x, arg z = , i за формулою (4)
|
p |
|
|
+ 2k |
|
+ 2k |
|
|
|
|
|
n |
|
|
|
|
|
|
|||
wk = |
( x) (cos |
+ i sin |
); k 2 0; n 1; |
|||||||
+ |
n |
n |
||||||||
утворюють множину всiх значень кореня n-го степеня з вiд'¹много чи-
ñëà z = x < 0. При цьому: |
головне значення кореня |
|
-ãî ñòå- |
||||||||
a) |
|
p |
|
|
|
|
|
|
|||
|
|
n |
x(cos |
|
|
|
|
||||
|
w0 = |
+ |
n |
+ i sin |
n |
) |
|
n |
|
||
пеня з вiд'¹много числа x не ¹ дiйсним |
8n > 1; |
|
|
|
|
|
|
|||||
á) ÿêùî n = 2m + 1, то ¹ ¹диним дiйсним значенням кореня n-ãî |
||||||||||||
степеня з вiд'¹много числа z = x ¹ число |
|
|
p |
|
|
|
|
|
||||
i ñàìå éîãî, à p |
|
|
+ 2m |
+ 2m |
|
n |
||||||
n |
|
|
n |
|
|
|
|
|
||||
wm = + ( x) (cos |
|
+ i sin |
|
) = |
|
( x); |
||||||
2m + 1 |
2m + 1 |
+ |
||||||||||
|
|
|
|
|
|
|
|
|
p |
|
, êîëè |
|
не головне значення, найчастiше позначають |
|
|
|
|
||||||||
n = 2m + 1, à x < 0;
â) ÿêùî n = 2m, то серед чисел wk нема¹ жодного дiйсного, тобто усi значення кореня n = 2m-го степеня з вiд'¹много числа z = x ¹
p
3 1 запишемо 1 як комплексне число в триго-
z = 1 = jzj(cos(arg 1) + i sin(arg 1)):
Ìà¹ìî j1j = 1; arg 1 = 0. Тодi за формулою (4) ма¹мо:
|
p |
|
|
2k |
|
2k |
|
|
|
||||||
wk = |
3 |
1 = (cos |
|
+ i sin |
|
); k 2 f0; 1; 2g: |
|
|
3 |
3 |
|||||
2.5. Комплекснi числа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
99 |
|||||||
|
|
|
|
|
|
|
|
Îòæå, w0 |
= cos 0 + i sin 0 = 1; w1 = |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
1 |
|
|
3 |
|
|
|
|
|||||||||
|
|
|
|
|
|
cos |
|
|
+ i sin |
|
|
= |
|
|
+ i |
|
|
|
|
|
; |
|
|
|
|||||
|
|
|
|
|
|
3 |
3 |
|
2 |
|
2 |
|
p |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
= |
1 |
|
|
i |
3 |
|
|||||||
|
|
|
|
|
|
w2 = cos |
|
|
+ i sin |
|
|
|
|
|
|
: |
|||||||||||||
|
|
|
|
|
|
|
3 |
3 |
2 |
|
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
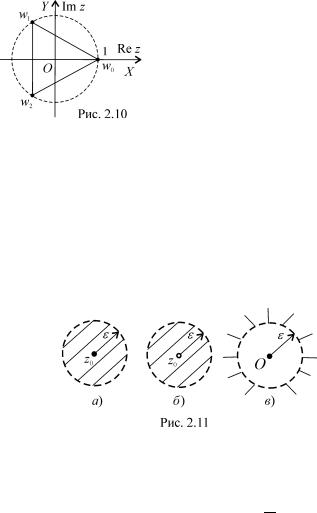
Точки w0; w1; w2 ¹ вершинами пра- |
|||||||||||||||||||||
|
|
|
|
|
|
вильного трикутника, вписаного в коло з |
|||||||||||||||||||||||
|
|
|
|
|
|
центром у точцi |
z = 0 òà ðàäióñîì r = |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
n jzj = 1 (ðèñ. 2.10). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.5.6. Околи точок комплексно¨ площини |
|
|
|
||||||||||||||||||||||||||
|
Îñêiëüêè jz1 z2j = |
(x1 x2)2 + (y1 y2)2 вiдстань мiж точка- |
|||||||||||||||||||||||||||
ìè |
(x1; y1) |
i |
(x2; y2) |
у площинi |
OXY |
, то природно вважати |
jz z0j = |
||||||||||||||||||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(z; z0) |
вiдстанню мiж числами |
z1 i |
|
z2, |
або мiж точками |
z1 i z2 ó |
|||||||||||||||||||||||
комплекснiй площинi C. При цьому множину = fz 2 C : jz z0j = rg доцiльно назвати колом, а множину K = fz 2 C : jz z0j < rg кругом з центром у точцi z0 i радiусом
Круг K називають також околом точки z0. Якщо, зокрема, r = ", то його називають також "-околом точки z0 у комплекснiй площинi C i позначають O"(z0) (рис. 2.11, а ).
Множину O"(z0) n fz0g називають проколеним околом ("-околом) точки z0 i позначають O" (z0) (рис. 2.11, б ), тобто це множина точок
z, що задовольняють нерiвнiсть
0 < jz z0j < ":
Якщо до C при¹днати так звану нескiнченно вiддалену точку 1, то дiстанемо розширену комплексну площину C = C [ f1g.
Околом (проколеним "-околом) нескiнченно вiддалено¨ точки 1 називають множину O" (1) = O"(1) = fz 2 C : jzj > "g (ðèñ. 2.11, â ).
П р и к л а д 5. Якщо " = 0; 01, то "-окiл та проколений "-окiл точки z0 = 1+i визначаються вiдповiдно нерiвностями jz 1 ij < 0; 01 та 0 < jz 1 ij < 0; 01; a "-окiл точки z0 = 1 нерiвнiстю jzj > 0; 01:
Множину E C називають обмеженою, якщо iсну¹ число H > 0 таке, що jzj 6 H 8z 2 E, тобто E лежить в деякому околi точки z = 0. У противному разi множину E називають необмеженою.
100 Роздiл 2. Множини дiйсних i комплексних чисел
2.5.7. Бiном Ньютона
Нарештi, доведемо важливу рiвнiсть, яка ма¹ назву бiнома Ньюто-
íà.
Насамперед введемо такi позначення: |
0! = 1 (0! нуль факторiал), |
|||||||
k |
n! |
|
|
|
|
|
kQ |
|
|
|
|
|
|
|
|
|
n |
n! = (n 1)!n (n! ен факторiал). Отже, n! = 1 2 : : : n = |
=1 k 8n 2 N. |
|||||||
Позначимо Cn = |
|
|
|
; k 2 |
0; n |
, òàê çâàíi áiíîìíi êîåôiöi- |
||
k!(n |
|
k)! |
||||||
¹íòè. |
|
|
|
|
|
|
|
|
Зокрема, C00 = 1; C10 |
= C11 = 1; C20 |
= 1; C21 = 2; C22 = 1; C30 = |
||||||
1; C31 = C32 = 3; C33 = 1 òîùî. |
|
|
||||||
Враховуючи цi позначення, запишемо вiдомi формули скороченого |
||||||||
множення у такому виглядi: |
|
kP |
P |
|
||||
|
|
|
|
|
||||
|
|
|
2 |
|
|
2 |
|
|
(a + b)2 = a2 + 2ab + b2 = C2ka2 kbk = C2kakb2 k; |
||||||||
|
|
|
=0 |
kP |
k=0 |
|
||
|
|
|
|
|
P |
|
||
|
|
|
3 |
|
3 |
|
||
(a + b)3 = a3 + 3a2b + 3ab2 + b3 = C3ka3 kbk = C3kakb3 k: |
||||||||
|
|
|
=0 |
k=0 |
||||
У зв'язку з цим виника¹ гiпотеза про правильнiсть такого твердження.
Теорема 1 (п р о б i н о м Н ь ю т о н а). Äëÿ áóäü-ÿêèõ комплексних
чисел a i b та для довiльного n 2 N правильна рiвнiсть |
|
|||
|
kP |
P |
|
|
|
n |
n |
|
|
|
(a + b)n = Cnkan kbk = |
Cnkakbn k; |
|
(5) |
|
=0 |
k=0 |
|
|
|
|
|
|
|
яку називають бiномом Ньютона .
I Скориста¹мося методом математично¨ iндукцi¨. Для n = 1 рiвнiсть (5) правильна.
Припустимо, що вона ¹ правильною для n = m i розглянемо випадок n = m + 1:
(a + b)m+1 = (a + b)m(a + b) = ( Pm Cmk am kbk)(a + b) =
k=0
|
P |
|
P |
|
|
|
m |
|
m |
|
|
|
= Cmk am+1 kbk + Cmk am kbk+1 = |
|
|||
|
k=0 |
k=0 |
|
|
|
= am+1 + Cmk am+1 kbk + |
|
Cmk am kbk+1 + bm+1 |
: |
||
|
kP |
|
P |
|
|
|
m |
|
m 1 |
|
|
|
=1 |
|
k=0 |
|
|
Зауважимо, що |
|
|
kP |
|
|
P |
P |
|
|
|
|
m |
m |
|
|
m |
|
|
Cmk am kbk+1 = Cmk 1am (k 1)bk = Cmk 1am+1 kbk; |
||||
k=0 |
k=1 |
|
|
=1 |
|
à òîìó
(a + b)m+1 = am+1 + Pm (Cmk + Cmk 1)am+1 kbk + bm+1: k=1
