
ifmion_kma_Mykhalin_Dujenkova(Mnozhyny)
.pdf1.6..Континуальнi множини. Iснування як завгодно велико¨ потужностi
Тепер зрозумiло, як можна утворити множину, потужнiсть яко¨ бiльша за континуальну.
1.6.8. Iсторична довiдка
Рiзницю мiж зчисленними та континуальними множинами першим помiтив чеський математик Б. Больцано. Поняття трансцендентного числа ввiв Л. Ейлер. Iснування трансцендентних чисел першим довiв у 1851 р. французький математик Ж. Лiувiлль (1809 1882). Наведенi нами доведення iснування трансцендентних чисел, як i всi iншi твердження даного параграфа належать Г. Кантору.
Трансцендентнiсть числа e довiв у 1873 р. французький математик
Ш. Ермiт (1822 1901), а числа у 1882 р. нiмецький математик
К. Лiндеман (1852 1939).
Творець теорi¨ множин Г. Кантор сформулював гiпотезу про те, що нема¹ потужностi, промiжно¨ мiж зчисленною та континуальною. Ця гiпотеза дiстала назву континуум-гiпотези. У 1939 р. австрiйський математик К. Гьодель (1906 1978) довiв, що нiякими логiчними мiркуваннями не можна спростувати цю гiпотезу. А в 1963 р. американський математик С. Коен (народився у 1934 р.) довiв, що континуум-гiпотезу не можна й довести нiякими логiчними мiркуваннями.
1.6.9. Зв'язок iз шкiльним курсом математики
Використовуючи факти, викладенi у цьому параграфi, вчитель математики зможе вiдповiсти на питання, яких числел бiльше: рацiональних чи дiйсних, дiйсних чи комплексних, рацiональних чи iррацiональних, алгебра¨чних чи трансцендентних.
Цi вiдповiдi ¹ дещо несподiваними, оскiльки навести конкретнi приклади чисел, яких менше (наприклад, рацiональних або алгебра¨чних) значно простiше, нiж чисел, яких бiльше (наприклад, iррацiональних
або трансцендентних).
1.6.10. Постановка проблем
Основнi проблеми, що стосуються потужностей, i вiдповiдi на якi корисно знати вчителевi математики, розв'язано. Постановку складнiших проблем та ¨х розв'язання вдумливий читач може знайти в спецi-
альнiй лiтературi, наприклад в [11] та [12].
1.6.11. Контрольнi запитання та завдання
1. Перевiрити, чи правильними ¹ такi твердження:
1)множина A незчисленна, якщо вона не ¹ зчисленною;
2)áóäü-ÿêèé ïðîìiæîê ha; bi ¹ континуальною множиною;
3)множина [a; b] n Q ¹ континуальною;
4)ÿêùî z0 трансцендентне число, то воно iррацiональне;
5)множина трансцендентних чисел заданого вiдрiзка ¹ континуальною;
52 |
Роздiл 1. Елементарнi факти теорi¨ множин |
6)множина деяких кiл (кругiв), що попарно не перетинаються i лежать у площинi XOY , може бути незчисленною множиною;
7)ÿêùî A незчисленна множина, то (A) = c;
8)множина всiх скiнченних пiдмножин множини N ¹ зчисленною;
9)об'¹днання не бiльш нiж зчисленно¨ кiлькостi множин, якi попарно не перетинаються, ¹ континуальною множиною;
10)множина всiх трансцендентних чисел ¹ кoнтинуальною;
11) множина всiх скiнченних пiдмножин вiдрiзка [0; 1] ¹ континуальною;
12)8n 2 N 9A : 2 (A) = n;
13)iсну¹ множина A òàêà, ùî 2 (A) = 1; 2 (A) = 3.
2. Довести данi твердження:
1)ÿêùî (A [ B) = c, òî (A) = c àáî (B) = c;
2)множина знакiв ? на площинi XOY , якi можуть мати рiзнi
розмiри, але попарно не перетинаються, ¹ континуальною;
3)множина комплексних трансцендентних чисел ¹ континуальною;
4)2 (N) = c, тобто 2a = c;
5)множина всiх дiйсних функцiй, визначених на вiдрiзку [a; b] ма¹ потужнiсть 2c = 2 ([0;1]).
3. Нехай = [0; 1], à S сукупнiсть пiдмножин множини , кожна
з яких ¹ або не бiльш нiж зчисленною, або континуальною. Довести, що S ¹ -алгеброю, а потужнiсть (A); A 2 S, ¹ ìiðîþ.
Ðîçäië 2
Множини дiйсних i комплексних чисел
У класичному математичному аналiзi здебiльшого розглядають чи- словi множини, тобто такi, елементами яких ¹ числа (дiйснi або комплекснi). У цьому роздiлi викладено елементи теорi¨ дiйсних та комплексних чисел.
2.1. Властивостi дiйсних чисел
Вводиться аксiоматичне поняття дiйсного числа. Розглядаються основнi та вивiднi властивостi дiйсних чисел; вводиться поняття супремуму, iнфiмуму, максимуму та мiнiмуму числово¨ множини; поняття модуля дiйсного числа та його властивостi й околу точки.
2.1.1. Визначальнi властивостi дiйсних чисел
Множиною дiйсних чисел назвемо довiльну множину R, яка задовольня¹ сформульованi нижче умови I IY, де a; b; c довiльнi елементи з R, якщо не сказано iншого. При цьому елементи множини R називатимемо дiйсними числами або просто числами.
I. Властивостi суми.
I1 (i ñ í ó â à í í ÿ ñ ó ì è): для будь-яких чисел a i b iсну¹ ¨х ¹дина сума c 2 R, яку позначають c = a + b;
I2 (ê î ì ó ò à ò è â í à, àáî ï å ð å ñ ò à â í à): a + b = b + a;
I3 (à ñ î ö i à ò è â í à, àáî ñ ï î ë ó ÷ í à): a + (b + c) = (a + b) + c; I4 (i ñ í ó â à í í ÿ í ó ë ÿ): iсну¹ число 0 2 R таке, що a + 0 = a.
При цьому 0 називають нульовим елементом àáî нулем R;
53
54 |
Роздiл 2. Множини дiйсних i комплексних чисел |
|
|
I5 (i ñ í ó â à í í ÿ ï ð î ò è ë å æ í î ã î ÷ è ñ ë à): äëÿ будь-якого числа |
|
a 2 R iсну¹ число ( a) таке, що |
a + ( a) = 0. При цьому ( a) |
|
називають протилежним числом до |
a. |
|
|
Операцiю вiдшукання суми a + b називають операцi¹ю додавання. |
|
II. Властивостi добутку.
II1 (i ñ í ó â à í í ÿ ä î á ó ò ê ó): для будь-яких чисел a i b iсну¹ ¹диний добуток c 2 R, який позначають c = a b або c = ab;
II2 (ê î ì ó ò à ò è â í à, àáî ï å ð å ñ ò à â í à): a b = b a;
II3 (à ñ î ö i à ò è â í à, àáî ñ ï î ë ó ÷ í à): a (b c) = (a b) c;
II4 (i ñ í ó â à í í ÿ î ä è í è ö i): iсну¹ число 1 òàêå, ùî 1 6= 0 i a 1 =
a.
При цьому 1 називають одиничним елементом, àáî одиницею;
II5 (i ñ í ó â à í í ÿ î á å ð í å í î ã î ÷ è ñ ë à): äëÿ будь-якого числа a 2
R; a 6= 0, iсну¹ число a 1 2 R òàêå, ùî a a 1 = 1. При цьому a 1 називають оберненим числом до a;
II6 (ä è ñ ò ð è á ó ò è â í à, àáî ð î ç ï î ä i ë ü í à): a (b+c) = a b+a c. Операцiю вiдшукання добутку називають операцi¹ю множення.
III. Властивостi упорядкованостi.
III1 (i ñ í ó â à í í ÿ â i ä í î ø å í í ÿ ¾ " ): на множинi R введено вiдношення "менше", яке позначають символом ¾ " , так, що для довiль-
них чисел |
a i b ма¹ мiсце одне й тiльки одне iз спiввiдношень: або |
|
a < b, àáî |
b < a, àáî a = b; |
|
III2 (ò ð à í ç è ò è â í i ñ ò ü â i ä í î ø å í í ÿ < ): ÿêùî a < b i |
b < c, |
|
òî a < c; |
|
|
III3 (ç â'ÿ ç î ê ó ï î ð ÿ ä ê î â à í î ñ ò i ç ñ ó ì î þ): ÿêùî a < b, òî |
||
a + c < b + c ; |
|
|
III4 (ç â'ÿ ç î ê ó ï î ð ÿ ä ê î â à í î ñ ò i ç ä î á ó ò ê î ì): ÿêùî a < b i |
||
0 < c, òî |
ac < bc, à ÿêùî a < b i c < 0, òî bc < ac. |
|
IY. Властивiсть неперервностi: якщо A i B непорожнi пiд- |
||
множини множини R i A 6 B в тому розумiннi, що a 6 b |
8a 2 A |
|
i b 2 B, то iсну¹ число c таке, що A 6 c 6 B, тобто a 6 c |
8a 2 A |
|
i c 6 b 8b 2 B. |
|
|
З а у в а ж е н н я. Спiввiдношення a 6 b розумiють так, що або |
||
a < b, àáî |
a = b. |
|
Властивостi I IY називають основними, àáî визначальними властивостями дiйсних чисел. х називають також аксiомами дiйсних чисел. Лише за допомогою цих аксiом можна довести всi iншi властивостi дiйсних чисел.
2.1.2. Координатна (числова) пряма
IIрикладом множини дiйсних чисел може бути множина точок так
звано¨ координатно¨, àáî числово¨ прямо¨.
Координатною прямою називають будь-яку пряму, на якiй зафiксовано двi рiзнi точки: O, що зобража¹ число 0 нуль, i A1, ùî
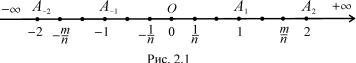
2.1. Властивостi дiйсних чисел |
|
55 |
зобража¹ число 1 одиницю. Вектор |
! |
|
OA1 |
з початком у точцi O i |
êiíöåì ó òî÷öi A1 çàä๠додатний напрям координатно¹ прямо¨, що познача¹ться стрiлкою (рис. 2.1).
Напрям, протилежний до додатного, називають âiä'¹ìíèì.
Для зображення числа 2 = 1+ 1 на координатнiй прямiй вiдкладають вiд точки A1 в додатному напрямi вiдрiзок A1A2, ðiâíèé âiäðiçêó OA1. Тодi точка A2 зобража¹ число 2. Так само буду¹мо точку A3, що зобража¹ на координатнiй прямiй число 3 i т.д. Аналогiчно зобража¹мо на координатнiй прямiй будь-яке натуральне число n 2 N.
Для зображення на координатнiй прямiй цiлого вiд'¹много числа ( n), що ¹ протилежним до натурального числа n, áóäó¹ìî íà êîîð-
динатнiй прямiй точку A n, симетричну точцi An вiдносно точки |
|
O |
||||||||
(äèâ. ðèñ. 2.1). |
|
|
|
|
|
|
|
|||
Для зображення на координатнiй прямiй рацiонального числа |
|
1 |
|
|||||||
n, |
||||||||||
|
|
|
|
|
|
|
||||
що ¹ оберненим до натурального числа |
n, äiëèìî âiäðiçîê |
OA1 íà n |
||||||||
рiвних вiдрiзкiв, одним з яких ¹ вiдрiзок |
OA 1 . Тодi точка |
A 1 |
зобра- |
|||||||
|
1 |
|
n |
n |
|
|
|
|
|
|
жа¹ число |
|
|
|
|
|
|
|
|
||
n |
|
|
m |
|
|
|
||||
Щоб зобразити на координатнiй прямiй рацiональне число |
|
|
|
|||||||
|
|
|
|
|
||||||
n , òðå- |
||||||||||
|
|
|
|
|
||||||
ба вiдкласти вiдрiзок OA 1 у додатномк напрямi m ðàçiâ, êîëè m > 0,
|
|
|
|
n |
|
|
|
|
i у вiд'¹мному напрямi |
( m) |
ðàçiâ, êîëè |
m < 0 |
. Тодi точка |
m |
|||
бражатиме число |
|
m |
|
|
|
A n çî- |
||
|
n |
|
|
|
|
|
||
Дiйсне число |
a, що не ¹ рацiональним, зобража¹ться на координа- |
|||||||
тнiй прямiй точкою Aa, що ¹ спiльною точкою вiдрiзкiв Aan Aa+n , äå an i a+n n-i рацiональнi наближення числа a вiдповiдно з недоста-
чею та з надлишком (див. п. 2.4.5).
Точки координатно¨ прямо¨ називають дiйсними числами, а дiйснi числа називають точками координатно¨ прямо¨. Таким чином отото-
жнюють поняття координатно¨ прямо¨ i множини R, точку координатно¨ прямо¨ i дiйсного числа.
2.1.3. Деякi iншi властивостi дiйсних чисел
Розглянемо iншi властивостi множини дiйсних чисел, якi будемо доводити, використовуючи основнi властивостi дiйсних чисел, розглянутi у п. 2.1.1.
Властивiсть 1 (п р о ¹ д и н i с т ь н у л я): нуль у множинi R ¹диний.
56 Роздiл 2. Множини дiйсних i комплексних чисел
I Äiéñíî, ÿêùî 0 i 0 нулi множини R, то за властивостями I4
òà I2 ìà¹ìî: 0 = 0 + 0 = 0 + 0 = 0 . J
Пропону¹мо читачевi самостiйно довести ¹динiсть одиничного, про-
тилежного та оберненого елементiв множини. |
|
Властивiсть 2 (п р о р о з в'я з о к р i в н я н н я |
x + a = b): x + a = |
b , x = b + ( a): Зокрема, x + a = a , x = 0. |
|
I Нехай x + a = b, тодi за властивостями I4 |
òà I5 äiñòà¹ìî x = |
x + 0 = x + (a + ( a)) = (x + a) + ( a) = b + ( a). |
|
Навпаки, якщо x = b+( a), òî x+a = (b+( a))+a = b+(a+( a)) = b + 0 = b, тобто x + a = b. J
Властивiсть 3 (п р о д о б у т о к x 0): x 0 = 0 8x 2 R.
I Згiдно з властивостями I4 òà II6, ìà¹ìî x 0 = x (0+0) = x 0+x 0, а тому за попередньою властивiстю x 0 = 0. J
За допомогою вiдношення < (менше) на множинi
ношення 6 (менше або рiвне), > (áiëüøå) òà > (áiëüøå àáî ðiâíå): a 6 b () a < b àáî a = b;
a > b () b < a;
a > b () a > b àáî a = b:
Число a називають: 1) додатним, ÿêùî a > 0; 2) âiä'¹ìíèì, ÿêùî a < 0; 3) недодатним, ÿêùî a 6 0; 4) íåâiä'¹ìíèì, ÿêùî a > 0.
Властивiсть 4 (п р о д о д а т н i с т ь 1): 1 > 0.
I Справдi, 1 6= 0 (за властивiстю II4), а тому за властивiстю III 1
1 > 0 àáî 1 < 0.
Якщо припустити, що 1 < 0, то за властивiстю III4 ç òîãî, ùî 1 < 0, виплива¹ 1 1 > 0 1 = 1 0 = 0 (останнi двi рiвностi випливають
з властивостей II2 i II4.
Àëå 1 1 = 1 (за властивiстю II4). Îòæå, 1 < 0 i 1 > 0. Дiстали протирiччя, яке й доводить, що 1 > 0. J
Íàñëiäîê 1 (ï ð î ç í à ê a 1). ßêùî a > 0, òî a 1 > 0, à ÿêùî a < 0, òî é a 1 < 0.
Властивiсть 5 (п р о з н а к д о б у т к у):
1) |
a b > 0 |
, a > 0 |
i b > 0 |
àáî a < 0 |
i b < 0; |
2) |
a b < 0 |
, a > 0 |
i b < 0 |
àáî a < 0 |
i b > 0. |
Зокрема, a a > 0 , a 6= 0. |
|
|
|||
I Äiéñíî, ÿêùî a b > 0, то за властивiстю 3 a 6= 0 i b 6= 0. IIрипустимо, що a > 0. Òîäi çà íàñëiäêîì 1 a 1 > 0, а тому за властивостями i 3 ма¹мо a 1(a b) > a 1 0 = 0: Звiдси, враховуючи властивостi
II3, II5 i II4, äiñòà¹ìî 1 b > 0 ) b > 0. Аналогiчно розгляда¹ться випадок, коли a < 0.
Навпаки, якщо a > 0 i b > 0 àáî a < 0 i b < 0, то за властивiстю ма¹мо a b > a 0 = 0. J
2.1. Властивостi дiйсних чисел |
57 |
||||||
Íàñëiäîê 2 (ï ð î ð i â í i ñ ò ü í ó ë þ ä î á ó ò ê ó): a b = 0 , a = 0 |
|||||||
àáî b = 0. |
|
|
|
|
|
|
|
Властивiсть 6 (п р о |
î á å ð í å í è é å ë å ì å í ò ä î á ó ò ê ó). ßêùî |
||||||
a 6= 0 i b 6= 0, òî (a b) 1 = a 1 b 1. |
|
||||||
I Äiéñíî, (a b) (a 1 b 1) = ((. a b) a 1) b 1 = ((a a 1) b) b 1 = |
|||||||
b b 1 = 1 ) (a b) 1 = a 1 b 1 J |
|
||||||
Аналогiчно властивостi 2 пропону¹мо читачевi довести, що коли |
|
||||||
a 6= 0, òî x a = b , x = b a 1. Зокрема, x a = a , x = 1. |
|
||||||
Рiзницею (b ìiíóñ a) чисел b |
i a називають суму b + ( a), ÿêó |
||||||
позначають b a. |
|
|
|
|
|
|
, |
Часткою (b ïîäiëåíî íà a) чисел b i a називають добуток b a 1 |
|
||||||
який позначають b : a àáî |
|
b |
|
|
b=a. |
|
|
|
a, àáî |
|
|||||
|
|
|
8a; b 2 R, à x a = b , x = b=a |
|
|||
Îòæå, x + a = b , x = b a |
|
||||||
8a; b 2 R : a 6= 0. |
|
|
|
|
|
|
|
Операцiю вiдшукання рiзницi b a називають вiднiманням, à îïå- |
|||||||
рацiю вiдшукання частки |
b=a дiленням. |
|
|||||
Отже, рiзниця b a iñíó¹ äëÿ âñiõ a; b 2 R, а частка b=a iñíó¹ äëÿ |
|||||||
òèõ a; b 2 R, äå a 6= 0. |
|
ù i ë ü í i ñ ò ü ì í î æ è í è R). ßêùî a < b, |
|||||
Властивiсть 7 (п р о |
|||||||
то iсну¹ число c таке, що |
a < c < b. |
|
|||||
I Дiйсно, число c = |
a + b |
2 (a; b). J |
|
||||
|
2 |
|
|
|
|||
Властивiсть 8 (п р о с у м у н е р i в н о с т е й). ßêùî a 6 b i c 6 d, òî a + c 6 b + d.
I За властивiстю III3, ÿêùî a 6 b, òî a + c 6 b + c, à ÿêùî c 6 d, òî c+b 6 d+b. Îòæå, a+c 6 b+c i c+b 6 d+b, а тому за властивiстю
III2 ìà¹ìî a + c 6 b + d. J
Пропону¹мо аналогiчно довести таку властивiсть.
Властивiсть 9 (п р о д о б у т о к н е р i в н о с т е й). ßêùî 0 6 a 6 b i 0 6 c 6 d, òî ac 6 bd.
Властивiсть 10 (п р о п р о т и л е ж н е ч и с л о д о п р о т ил е ж н о г о ч и с л а): ( a) = a:
I Справдi, згiдно з властивiстю I 4 ìà¹ìî ( a) + ( ( a)) = ( a) + a = 0 òîäi é òiëüêè òîäi, êîëè ( a) = (( a) + a) + ( ( a)) = (( a) + ( ( a))) + a = a (тут використано властивостi 2 та I 3). J
Властивiсть 11 (к р и т е р i й п о р i в н я н н я ): a > b ,
a b > 0. Аналогiчний критерiй ма¹ мiсце для спiввiдношень ¾", " 6 " i ¿".
I ßêùî a > b, то за властивiстю 8 ма¹мо a + ( b) > b + ( b) ) a b > 0. Навпаки, якщо a b > 0, знову ж таки за властивiстю 8
(a b) + b > a + b ) a + (b b) > b ) a > b. J
58 Роздiл 2. Множини дiйсних i комплексних чисел
Пропону¹мо читачевi самостiйно довести, що: (a 1) 1 = a 8a 6= 0; a a > 0 8a 2 R; a a > 0 8a 6= 0; ( a) = ( 1) a 8a; ( 1) ( 1) = 1; a(b c) = ab bc.
2.1.4.Супремум, iнфiмум, максимум i мiнiмум числово¨ множини
Множину E називають числовою, ÿêùî E R. Геометрично число-
ву множину зображають деякими точками координатно¨ прямо¨ (див. рис. 2.2).
Числову множину називають обмеженою зверху (знизу), якщо iсну¹ число a 2 R òàêå, ùî E 6 a (E > a), тобто x 6 a (x > a) 8x 2 E. Ïðè
цьому число a називають верхньою (нижньою) межею множини E. Якщо, крiм того, число a 2 E, то його називають найбiльшим
(найменшим) числом множини E, àáî максимумом (мiнiмумом) öi¹¨
множини i позначають max E (min E).
Геометрично точки обмежено¨ зверху (знизу) числово¨ множини лежать лiвiше (правiше) вiд точки a або збiгаються з нею.
Множину називають обмеженою, якщо вона обмежена i зверху, i знизу.
Найменшу з усiх верхнiх меж ножини E називають ¨¨
ньою межею, àáî верхньою гранню, àáî супремумом sup E.
Найбiльшу з усiх нижнiх меж ножини E називають ¨¨ точною нижньою межею, àáî нижньою гранню, àáî iнфiмумом i позначають inf E.
Iз латинi supremum означа¹ найвищий, а infimum найнижчий. Таким чином, супремум "схожий"на максимум, а iнфiмум на мiнiмум множини. Вони стають ними, коли належать множинi A.
Теорема 1 (В е й ¹ р ш т р а с с а п р о i с н у в а н н я sup E ò à inf E).
Якщо непорожня множина E R обмежена зверху (знизу), то вона ма¹ супремум (iíôiìóì).
I Якщо множина ? 6= E 2 R обмежена зверху, то множина E = fx 2 R : x верхня межа E g непорожня i E 6 E . Òîìó çà властивiстю неперервностi iсну¹ дiйсне число таке, що E 6 6 E . Звiдси виплива¹, що верхня межа E, à òîìó 2 E , îòæå, = min E , тобто = sup E.
Мiркування для inf E аналогiчнi. J
Íàñëiäîê (ê ð è ò å ð i é ñ ó ï ð å ì ó ì ó ò à i í ô i ì ó ì ó):
= sup E òîäi é |
|
òàêå, ùî |
|
x 6 |
8x 2 E |
|
|
òiëüêè òîäi, êîëè |
|
|
i для будь-якого |
||
" > 0 iсну¹ число x |
|
|
x > "; |
|
|
|
= inf E òîäi é |
|
òàêå, ùî |
|
x > 8x 2 E |
|
|
|
òiëüêè òîäi, êîëè |
|
|
i для будь-якого |
||
" > 0 iсну¹ число x |
|
x < + " (ðèñ. 2.2). |
|
|||

2.1. Властивостi дiйсних чисел |
59 |
I Справдi, згiдно з теоремою 1, = sup E ¹ верхньою межею E, à òîìó x 68x 2 E. Якщо припустити, що iсну¹ таке " > 0, ùî
x 6 " 8x 2 E, то число " буде верхньою межею E i " < ,
тобто не ¹ найменшою верхньою межею, що неможливо. Отже, 8" > 0 9 x 2 E : x > ". J
Таким чином, правiше за = sup E нема¹ точок з множини E, проте iснують точки з E (вони можуть бути як завгодно близькими до ), зокрема сама точка , якi лежать правiше за " 8" > 0.
Аналогiчнi висновки можна зробити щодо inf E. Пропону¹мо чита- чевi зробити це самостiйно.
Якщо множину R доповнити ще двома елементами +1 òà 1, вважаючи, що 1 < a < +1 8a 2 R, то дiстанемо розширену множину дiйсних чисел R = R [ f 1; +1g. При цьому 1 òà
+1 називають невласними числами "плюс нескiнченнiсть\ òà "мiнус нескiнченнiсть\ âiäïîâiäíî.
Множину E R, що не ¹ обмеженою зверху (знизу), називають
необмеженою зверху (знизу). При цьому вважають, що sup E = +1
(inf E = 1).
Ï ð è ê ë à ä 1. sup N = sup Z = sup Q = sup R = +1; inf N = min N = 1; inf Z = inf Q = inf R = 1; inff1; 1=2; 1=3; : : : ; 1=n; : : : g = 0, supf1; 1=2; 1=3; : : : ; 1=n; : : : g = maxf1; 1=2; 1=3; : : : ; 1=n; : : : g = 1.
Використовуючи вiдношення ¾ \, ¿\, " 6 \ òà " > \, можна ввести поняття числового промiжку ha; bi, ùî ìîæå áóòè:
âiäðiçêîì [a; b] = fx 2 R : a 6 x 6 bg;
ïiââiäðiçêîì [a; b) = fx 2 R : a 6 x < bg;
iнтервалом (a; b) = fx 2 R : a < x < bg;
пiвiнтервалом (a; b] = fx 2 R : a < x 6 bg, äå a i b фiксованi числа з R i a 6 b.
Зокрема, [a; a] = fag, [a; a) = (a; a) = (a; a] = ?.
Геометрично числовi промiжки зображають вiдповiдними промiжками координатно¨ прямо¨ (рис.2.3).
Враховуючи вказанi означення, можна вважати, що R = ( 1; +1),
[ 1; +1] = R, [ 1; b) = ( 1; b) [f 1g, (a; +1] = (a; +1) [f+1g.

60 Роздiл 2. Множини дiйсних i комплексних чисел
Ï ð è ê ë à ä 2. sup [a; b] = sup [a; b) = b, inf [a; b] = inf (a; b] =
a;
max[a; b] = b; min [a; b] = a; max [a; b) i min (a; b] не iснують.
Îòæå, ÿêùî iñíó¹ max E (min E), òî max E = sup E (min E = inf E), проте на вiдмiну вiд max E i min E супремум та iнфiмум множини E iснують завжди. У цьому й поляга¹ властивiсть неперервностi множини дiйсних чисел .
2.1.5. Модуль дiйсного числа
Модуль (абсолютну величину) дiйсного числа x позначають jxj i визначають рiвнiстю
n
jxj =
Ï ð è ê ë à ä 3. j 3 j
x; êîëè x > 0;x; êîëè x < 0:
= 3; j 2; 1 j = 2; 1; j 0 j = 0. Геометрично jxj öå âiä-
стань точки x координатно¨
прямо¨ вiд початку (точки 0) цi¹¨ прямо¨, тобто довжина вiдрiзка [0; x], êîëè x > 0, àáî
âiäðiçêà [x; 0], êîëè x < 0. Указану вiдстань позначають (x; 0) (ðèñ. 2.4).
Аналогiчно jx yj це вiдстань (x; y) мiж точками x i y координатно¨ прямо¨, тобто довжина вiдповiдного вiдрiзка (рис. 2.5).
Сформулю¹мо найпростiшi властивостi модуля .
1)Íåâiä'¹ìíiñòü: jxj > 0;
2)ðiâíiñòü íóëþ: jxj = 0 , x = 0;
3)порiвняння jxj з x та x : jxj > x, jxj > x;
4) |
симетричнiсть: jxj = j xj; |
|
|
|
|
|
|
|
5) |
модуль суми та рiзницi: jjxj jyjj 6 jx yj 6 jxj + jyj; |
|||||||
6) |
модуль добутку та частки: jx yj = jxj jyj; |
y |
= jjyjj; y 6= 0; |
|||||
|
|
|
|
x |
|
|
x |
|
7) |
розв'язування нерiвностей з модулем : |
8 |
x0 |
|
R |
i a > 0 |
||
|
|
|
2 |
|
|
|
|
|
jx x0j < a , |
x0 a < x < x0 + a , x 2 (x0 a; x0 + a); |
jx x0j 6 a , |
x0 a 6 x 6 x0 + a , x 2 [x0 a; x0 + a]; |
