SimulationPhysProc_1_81

Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Обнинский государственный технический университет атомной энергетики (ИАТЭ)

Факультет естественных наук

Ф.И. Карманов, А.А. Суворов

Численное решение дифференциальных уравнений

вфизике

сиспользованием пакета

MathCAD

Учебное пособие по курсу

«Вычислительные методы в инженерных расчетах»

ОБНИНСК 2007

Глава 1. Колебательные уровни двухатомной молекулы

Рассчитаем фазовый портрет и уровни энергии колебательного движения двухатомной молекулы на основе полуклассического квантования молекулярных колебаний.

Рассмотрим задачу о поиске уровней энергии колебательного движения двухатомной молекулы в приближении Борна-Оппенгеймера [1-4]. При анализе задачи будем предполагать, что при большом различии масс электронов и ядер электроны всегда успевают отреагировать на медленные перемещения ядер и потому взаимодействие ядер молекулы между собой можно описывать с помощью некоторого феноменологического потенциала взаимодействия нейтральных атомов, зависящего только от относительного расстояния между ядрами. Этот потенциал должен быть притягивающим на больших расстояниях и, в силу кулоновского отталкивания ядер и из-за действия принципа Паули для электронов, должен обеспечивать эффективное отталкивание на малых расстояниях.

В качестве такого потенциала часто используются потенциалы Ленар- да-Джонса или Морса. Если обозначить через a –характерный размер области действия потенциала и Vо – глубину потенциальной ямы, то зависимость V(r) для потенциала Ленарда-Джонса (потенциал 6-12) имеет вид:

где точка минимума потенциала связана с параметром a соотноше-

нием

rmin = a 6 2 .

Потенциал Морса может быть представлен в виде:

V(r) = Vo 1 − exp −β (r − rmin) 2 − 1 ,

где β – свободный параметр.

Одномерное уравнение Шредингера для волновой функции Ψn коле- бательного движения двухатомной молекулы имеет вид:

3

Здесь m – приведенная масса двух ядер, а n – номер колебательного состояния. Для некоторых потенциалов, например, Морса, эта задача может быть решена точно (см. [2]), но, учитывая большую массу ядер, их движение можно считать квазиклассическим, и искать спектр энергий En колебательного движения, используя полуклассические правила квантования Бора-Зоммерфельда [3,4].

Правило квантования

Ограниченное классическое движение в потенциале V(r) может происходить при энергии – Vo < E < 0. Расстояние между ядрами периодически изменяется в пределах между rin и rout – классическими точками поворота. Для заданной полной энергии E

E = p2 + V(r) 2 m

импульс p относительного движения выражается как функция r

p(r) = ± 2 m (E − V(r)) .

Для того чтобы проквантовать движение и получить приближенные значения энергии, рассмотрим безразмерное действие [1,3]. Выполняя интегрирование вдоль замкнутой траектории, получаем

где n – заданное неотрицательное целое число, а границы rin и rout интегрирования определяются из условия обращения в нуль подынтегральной функции. Полученное нелинейное уравнение для E определяет уровни энергии в заданном потенциале.

Фазовый портрет колебаний молекулы водорода

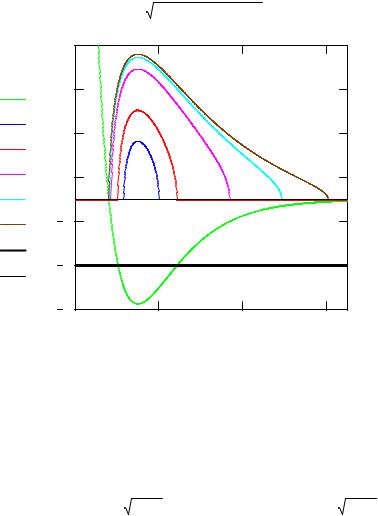
Согласно экспериментальным данным [3], для молекулы водорода глубина потенциальной ямы и положение минимума потенциала соответственно равны Vо = 4.747eV и rmin = 0.7417A. Энергии первых 15-ти колебательных состояний будут приведены ниже при сравнении с результатами расчетов для потенциала Морса с параметром β =2. График потенциала показан на рис.1. Границы движения соответствуют точкам пересечения кривой потенциала с одним из уровней энергии, например, E = –3.017 eV. Для построения фазовых траекторий рассчитаем зависимость импульса от координаты при заданной энергии.

4

Уровни энергии молекулы водорода

Переходя к безразмерным переменным с помощью соотношений:

5

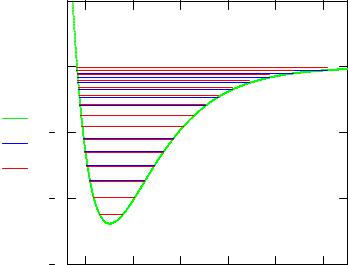
Сравнение результатов расчета с экспериментальными данными показывает, что значения нижних уровней энергии воспроизводятся достаточно хорошо при β = 2, а высоковозбужденные состояния заметно отличаются. Оптимальное значение параметра β может быть выбрано, например, на основе минимизации среднеквадратичного отклонения расчетных и экспериментальных значений уровней энергии.

6

Упражнения

1.Рассчитайте уровни энергии молекулы водорода, решая нелинейное уравнение методом дихотомии, методом Ньютона или методом секущих (см. [5,6]).

2.Предложите способ выбора начального приближения в методе Ньютона без предварительного расчета, например, по методу дихотомии. Оцените скорость сходимости по числу верных знаков корня, получающихся после каждой итерации.

3.Оцените влияние способа вычисления интегралов при определении функции F(ε,n) и ее производной. Среди встроенных функций вычисления интегралов в контекстном меню выберите пункты: Romberg, Adaptive или Singular Endpoint и проанализируйте результаты расчета.

4.Найдите оптимальное значение параметра β методом наимень- ших квадратов на основе минимизации среднеквадратичного отклонения рассчитываемых и экспериментальных значений уровней энергии.

7

5. Покажите, что в потенциале Ленарда-Джонса с параметрами rmin= 0.74166 A и Vo = 4.747 eV для молекулы H 2 существует только шесть уровней энергии. Вычислите эти энергии.

6. Найдите уровни молекулы H2 в потенциале Кратцера (см. [2], с. 189) V(r) = −Vo ar 2 − ar , где a = 0.74166 A, Vo= 4.747 eV.

7. Рассчитайте уровни энергии молекулы HD, считая, что потенциал взаимодействия – есть потенциал Морса с параметрами молекулы H2. (Оцените изотопический сдвиг уровней в молекуле HD).

8. Колебательные уровни энергии двухатомной молекулы, находящейся в основном электронном и вращательном состояниях, с хорошей точностью могут быть представлены в модели ангармонического осцилля-

тора [7]:

En = −Vo + w (n + 0.5) − ax (n + 0.5)2 ,

где w – частота гармонических колебаний (eV), ax – постоянная ангармонизма (eV). Данные о некоторых двухатомных молекулах представлены в таблице. (amu = 931.49 МeV).

Для молекулы H2 оцените число колебательных уровней и их значения

на основе этой информации. Сравните результаты расчета состояний в потенциале Морса, модели ангармонического осциллятора и экспериментальные данные.

9. Для молекул D2 и I2 оцените число колебательных уровней в модели ангармонического осциллятора [7] и рассчитайте уровни энергии в потенциале Морса. Найдите оптимальное значение параметра β.

10. Проанализируйте характер изменений в спектрах двухатомных молекул (число уровней, их взаимное расположение, частоты для низких колебательных состояний, энергию нулевых колебаний, энергию диссоциации и т.д.) при увеличении массы молекулы.

8

Глава 2. Классическое рассеяние на силовом центре

Используя законы сохранения энергии и момента импульса, рассчитаем связь прицельного параметра и угла отклонения частицы в центральном потенциальном поле. На примере потенциала ЛенардаДжонса найдем дифференциальное сечение рассеяния как функцию угла рассеяния.

Связь угла отклонения и прицельного параметра

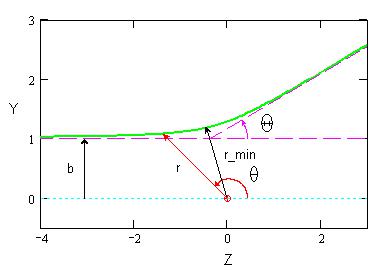
Пусть частица массы m с энергией E рассеивается (см. рис. 1) на неподвижном силовом центре c потенциалом V(r). Законы сохранения энергии и момента импульса частицы имеют вид [3,10]:

L = m v b = m r2 d θ dt

Выбирая координату r в качестве независимой переменной вместо времени t, можем записать

Рис. 1. К описанию рассеяния частицы на силовом центре

9

Выражая угловую скорость и радиальную компоненту линейной скорости из соответствующих законов сохранения, получим:

Принимая во внимание тот факт, что θ = π на входном участке траектории при r = ∞, и угол θ убывает вдоль траектории, а траектория сим-

метрична относительно точки r = r_min – расстояния наибольшего сближения частицы и силового центра, выполним интегрирование по r в предыдущем соотношении в пределах от ∞ до r_min.

Входящая сюда величина r_min(b,E) является функцией прицельного параметра и энергии и определяется как наибольший корень уравнения

Обычно влиянием потенциала на траекторию частицы на больших расстояниях можно пренебречь и этот факт использовать для выбора r_max

– верхнего предела интегрирования. Поскольку

b

представим выражение для угла отклонения как разность двух функций, которые при r > r_max компенсируют друг друга.

10