
SimulationPhysProc_1_81
.pdftime := |
q10 |
time = 6 × 10 |
− 14 |
s |
c := 3 10 |
18 A |
time := c time |
−v10 |
|
s |
|||||
Вычисляя компоненты градиента потенциальной энергии, определим |
|||||||
действующие на частицы силы |
|
|
|
|
|||
d |
|
|
d |
|
|
||||
F23(q1,q23) := − |
|
|
UJ(q1,q23) |
|
F1(q1,q23) := − |
|
|
UJ(q1,q23) |
|
|
|
||||||||
dq23 |
|
|
dq1 |
|
|
||||
и запишем уравнения движения в форме |
|
|
|
1 |
|
|
||
d |
q1 = v1 |
d |
v1 = |
|
F1(q1,q23) |
|||
|
|
|
||||||
dt |
dt |
μ1 |
||||||
d |
q23 = v23 |
d |
v23 = |
|
1 |
F23(q1,q23) . |
||
|
|
|||||||
dt |
dt |
|
|
μ23 |
||||
Для решения уравнений движения воспользуемся одной из встроенных функций решения систем дифференциальных уравнений, например, функцией Rkadapt(). Векторы начальных данных и правой части определим так, чтобы в одном расчете получить данные для двух траекторий, отвечающих максимальному и минимальному удалению атомов в молекуле в начальном состоянии. Пусть
e23 := −1 |
|
|
v230 := 0 |
X0 := q01(e23,v230) |
X1 := q02(e23,v230) |
||||||||||||||
q10 := 4 |
|
|
v10 := −0.5 1014 |
1 |
|
time := |
q10 |
|
|
|
time = 2.4 × 105 |
||||||||
|
|
c |
|
−v10 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1 |
|
|
|||
|
1.872 |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|||||
X = |
|
|
|
|
q10 |
|
|
|
|
|
|
|
|
|
|
||||
|
0.414 |
|
|
|
|
|
|
|
1 |
F1(f0,f2) |
|
||||||||
|
|
|
|
|
|
|
|
v10 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
μ1 |
||||||||
|
k := 0 .. 1 |
|
f |
:= |
Xk |
|
D(t,f) := |
|
f3 |
|
|
||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v230 |
|
|
|
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
F23 f ,f |
|
|||||||
|
Rkadapt(fk,0 ,time,200 ,D) |
|
|
|
|
|
|
||||||||||||
Zk := |
|
|
|
|
|
μ23 |
(0 |
2) |
|
||||||||||
|
0 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
{201,5} |
||||
t := (Z0) |
|
|
c |
sec |
|
|
|
|
|
q1m := (Z0) |
|
|
Z = |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{201,5} |
|||
Для двух этих траекторий находим расстояния в парах (23) и (12) |
|
||||||||||||||||||
|
q23m := (Z0)3 |
A |
|
|
|
q12m := (Z0)1 − 0.5 (Z0)3 |
A |
|
|||||||||||
|
q23n := (Z1)3 |
A |
|
|
|
q12n := (Z1)1 |
− 0.5 (Z1)3 |
A |
|
||||||||||
41
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
q23m |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q12m |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
q23n |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q12n |
1 |
|
|
|
|
|
|
|
|
|
|
q0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
. |
|
14 |
. |
14 |
|
. |
|
14 |
. |
14 |
|
0 |
2 |
10 |
6 |
10 |
||||||||
|
|
|
4 10 |
t |
|
|
8 10 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
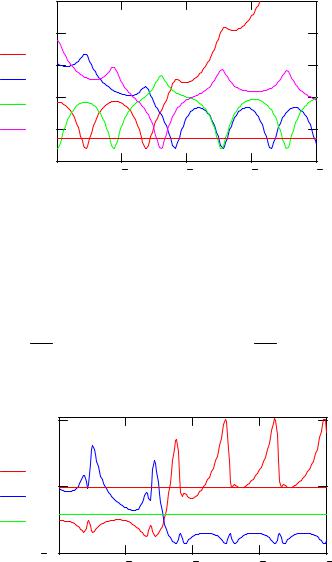
Рис. 4. |
Координаты в парах частиц в зависимости от времени |
||||||||||||
Учитывая связь импульсов, |
находим для первой траектории скорости |
||||||||||||||
v23 и v12, |
полные энергии в парах частиц с использованием функции |
||||||||||||||
Морса, и полную энергию системы как функции времени. |
|
|
|
|
|||||||||||
v23m := (Z0)4 |
v12m := (Z0)2 − 1 |
(Z0)4 |
|
|
E1m := |
μ1 |
(Z0)2 2 |
||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
E23m := μ23 v23m2 + V(q23m) |
E12m := |
μ12 v12m2 + V(q12m) |
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Etotm := |
μ23 |
v23m2 + E1m + |
→ |
|
|
||||||||
|
|
UJ(q1m,q23m) |
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E23m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E12m |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Etotm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
. |
|
14 |
. |
14 |
|
. |
|
14 |
. |
|
14 |
|
|
0 |
2 |
10 |
6 |
10 |
|
|
||||||||
|
|
|
4 10 |
t |
|
|
8 10 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
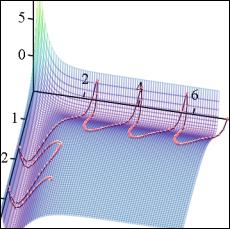
Рис. 5. Полные энергии в парах частиц и для всей системы |
|
||||||||||||||
42
Как видно из рис. 4, при выбранных начальных условиях траектория атома и молекулы, отвечающая максимальному удалению атомов в молекуле в начальном состоянии, является реакционноспособной. Исходная молекула в паре 23 распадается и образуется новая из атомов 1 и 2. Во втором варианте, соответствующем минимальной точке поворота в молекуле, обмена атомами не происходит.
Представленные на рис. 5 энергии тоже свидетельствуют о происшедшем обмене атомами, причем образовавшаяся молекула имеет меньшее значение полной энергии, чем имела молекула до столкновения, а улетающий атом имеет энергию выше, чем налетающий атом имел до столкновения. Отметим, что потенциальная энергия системы не равна сумме парных потенциальных энергий, задаваемых функцией Морса. Постоянство во времени полной энергии системы говорит о приемлимом уровне точности решения системы уравнений движения.
Построение динамической траектории
Вычислим потенциальную энергию системы вдоль реакционной траек-
тории по формуле: |
→ |
|
Um := U(q12m,q23m,q12m + q23m) |
и построим траекторию как совокупность точек (q12m,q23m,Um).
Φ,(q12m,q23m,Um)
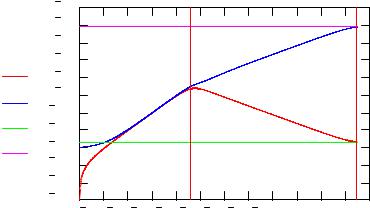
Рис. 6. Траектория на поверхности потенциальной энергии для реакции Н + Н2 –> Н2 + Н в коллинеарной геометрии. Рассчитанный участок начинается при q12= 4 А, q23= 1.87 А, проходит около седловой точки
(0.986 А, 0.986 А) и заканчивается при q12= 0.54 А и q23= 7.35 А
43
Упражнения
1. Для рассчитанной выше нереакционноспособной траектории проанализировать зависимость от времени энергий в парах частиц и полной энергии системы. Построить эту траекторию на поверхности потенциальной энергии.
2. Исходя из условия обращения в нуль производных потенциальной энергии Φ(q12,q23) по обеим переменным, для реакции обмена атома и молекулы водорода найти координаты седловой точки поверхности, используя один из методов поиска экстремума функции многих переменных (см. [5,6]). Подготовить программу расчета координат седловой точки и проверить результаты работы Вашей программы с помощью встроенных функций MathCAD. Ab initio расчет дает для координат седловой точки значения (0.928 А, 0.928 А).
3.Путь химической реакции – такая траектория на поверхности потенциальной энергии, которая соответствует минимальной энергии реакции. Стартуя из седловой точки с нулевой скоростью и двигаясь вдоль антиградиента потенциальной энергии с близкой к нулю скоростью, можно вычислить координаты точек траектории, соединяющей начальное (реагенты) и конечное (продукты) состояния реакции – координату реакции. Для реакции обмена атома и молекулы водорода рассчитать и построить сечение поверхности потенциальной энергии вдоль координаты реакции (длины дуги) и оценить разность энергий реагента и переходного состояния в седловой точке – высоту классического барьера реакции как оценку энергии активации реакции. Построить путь химической реакции на поверхности потенциальной энергии.
4.Пусть атомы в молекуле двигаются только вдоль ее оси, а налетающий атом приближается к молекуле водорода вдоль перпендикуляра к оси, проходящего через центр молекулы. В координатах Якоби (q 1, q23,
α= π/2) построить поверхностный и контурный графики потенциальной энергии. Оценить положение седловой точки и высоту классического барьера реакции. Используя один из методов поиска экстремума функции многих переменных (см. [5,6]), подготовить программу и рассчитать координаты седловой точки.
5.Для реакции Н + Н2 –> Н2 + Н в координатах Якоби при α = π/2, стартуя из седловой точки, рассчитать обе ветви пути химической ре-
акции в области q1 > 0. Вычислить потенциальную энергию вдоль пути химической реакции и построить ее график.
6.Рассчитать динамические траектории в переменных (q1, q23) для нескольких начальных условий в реакции Н + Н2 –> Н2 + Н при движении налетающего атома по перпендикуляру к оси молекулы через ее
44
середину. Проанализировать динамику изменения во времени энергии в парах частиц и полной энергии системы. Построить траектории на поверхности потенциальной энергии в интервале (-5 A < q 1 < 5 A) и (0.5 A < q23 < 2.5 A).
7. Сконструировать LEPS -модель поверхности потенциальной энергии для реакции F + Н2 –> FН + Н, используя для определения кулоновских и обменных интегралов следующие значения параметров парной потенциальной функции Морса для соответствующих пар атомов F и H
DFH = 6.1339 eV, |
βFH = 2.2189 1/A, |
q0FH = 0.9168 A, |
SFH = 0.167, |
DHH = 4.7547 eV, |
βHH = 1.9420 1/A, |
q0HH = 0.7419 A, |
SHH = 0.061. |
8. Для модели поверхности потенциальной энергии из задачи 7 в коллинеарной геометрии для реакции F + Н2 –> FН + Н построить поверхностные и контурные графики потенциальной энергии, оценить положение седловой точки, высоту классического барьера и тепловой эффект реакции. Ab initio-расчет дает ( EF-H2 –EFH-H = 1.49 eV, Ec = 0.074 eV ).
9. Используя один из методов поиска экстремума функции многих переменных (см.[5,6]) для реакции F + Н2 –> FН + Н в коллинеарной геометрии подготовить программу расчета координат седловой точки и проверить результаты работы Вашей программы с помощью встроен-
ных функций MathCAD. Ab initio-расчет дает (q12 =1.54А, q23 = 0.76А).
10. Для реакции F + Н2 –> FН + Н в коллинеарной геометрии, начиная от седловой точки, рассчитать обе ветви пути химической реакции, вычислить потенциальную энергию вдоль пути химической реакции и построить ее график.
11. Рассчитать динамические траектории в переменных (q1, q23) для нескольких начальных условий в реакции F + Н2 –> FН + Н в коллинеарной геометрии. На основе вычислительного эксперимента найти начальные условия, при которых реализуется реакционноспособная траектория, пересекающая переходное состояние. Проанализировать динамику изменения во времени энергии в парах частиц и полной энергии системы. Построить траектории на поверхности потенциальной энергии.
12. В переменных Якоби (q1, q23, α ) построить поверхностные и контурные графики потенциальной энергии в реакции F + Н2 –> FН + Н как сечения для нескольких значений α. Подготовить программу расче- та координат седловых точек функции трех переменных и проверить результаты работы Вашей программы с помощью встроенных функций
MathCAD. Используя встроенные функции Minimize() и Maximize() и
формулируя ограничения на область изменения их аргументов, рассчитать положения и уровни потенциальной энергии каналов реакции.
45
Глава 5. Кинетика точечных дефектов в твердых телах
Если материал интенсивно облучается, то в нем происходит постоянная генерация точечных дефектов (вакансий и межузельных атомов), причем с одинаковой скоростью. Пусть дефекты равномерно распределяются по объему материала, так что можно говорить об усредненных по объему концентрациях вакансий и межузлий.
Рассмотрим временную эволюцию усредненных по пространству концентраций одномерных дефектов – вакансий и межузельных атомов в кристалле никеля на диффузионной стадии эволюции дефектной структуры.
Уравнения и параметры модели
Будем предполагать, что дефекты образуются в единице объема за счет внешних источников (ускоритель, высоковольтный электронный микроскоп) со скоростями
Gi := 10− 3 dpa s− 1 Gv := 10− 3 dpa s− 1 .
Пусть энергии активации миграции для вакансий и межузельных атомов и температура кристалла Ni равны
Ei := 0.15 eV Ev := 1.3 eV Temp := 673 K .
Температурная зависимость коэффициентов диффузии имеет вид
Temp := Temp 0.8617 10− 4 eV |
|
D0i := 0.01 cm2 s− 1 |
D0v := 0.92 cm2 s− 1 |
−Ei |
−Ev |
||||
Di := D0i exp |
|
|
Dv := D0v exp |
|
. |
Temp |
Temp |
||||
Точечные дефекты взаимодействуют с протяженными дефектами - дислокациями и порами (уходят на стоки) и рекомбинируют между собой. Пусть параметры дислокаций и пор, а также значения параметра преференса, учитывающего более сильное упругое взаимодействие дислокаций с межузельными атомами, чем с вакансиями, имеют значения
Zi := 1.02 |
Zv := 1.0 |
Sdisl := 108 cm− 2 |
Svoid := 108 cm− 2 |
Ki := Di (Zi Sdisl + Svoid) |
Kv := Dv (Zv Sdisl + Svoid) |
μr := 8 1016 cm− 2 |
R := μr (Di + Dv) . |
Система уравнений точечной кинетики для концентрации вакансий Cv и межузельных атомов Ci имеет вид ([15-16]):
46
d |
d |
dtCi = Gi − R Ci Cv − Ki Ci |
dtCv = Gv − R Ci Cv − Kv Cv . |
Если принять энергию формирования вакансии равной Evf := 1.6 eV то начальные термодинамически равновесные концентрации вакансий и межузельных атомов можно выбрать на уровне
|
−Evf |
− 12 |
|
− 3 |
||
z0 := exp |
|
|
|
z0 = 1.042 × 10 |
cm |
|
Temp |
|
|||||
|
y0 = 1.042 × 10− 15 |
cm− 3 . |
||||
y0 := 0.001 z0 |
||||||
Время расчета и асимптотические значения концентраций
Если не учитывать реакций образования комплексов дефектов, то при малых временах введения в материал точечных дефектов их концентрации растут во времени от начальных концентраций примерно по линейному закону, определяемому скоростью генерации Gv и Gi. В процессе
накопления дефектов возрастает роль реакции рекомбинации вакансий и межузлий. Поскольку рекомбинация одинакова как для вакансий, так и для межузлий, то зависимости концентраций почти не отклоняются от линейных. Далее начинает сказываться роль процессов ухода дефектов на стоки и при определенных условиях возможно установление новых, отличных от термодинамически равновесных, стационарных концентраций дефектов. Полагая в уравнениях производные по времени равными нулю, можно найти стационарные концентрации C0v, C0i [16].
C0i := |
Ki Kv + R (Gv − Gi) |
|
C0v := |
Ki Kv + R (Gi − Gv) |
|
|
||||||
|
|
2 R Ki |
|
|
|
|
|
2 R Kv |
|
|
||
|
|
|
Gi Kv |
|
|
|
|
|
|
Gv Ki |
|
|
C0i := |
C0i |
1 + |
|
|
|
− 1 |
C0v := |
C0v |
1 + |
|
|
− 1 |
|
2 |
|
|
2 |
||||||||
|
|
|
R Ki C0i |
|
|
|
|
|
R Kv C0v |
|
||
|
|
|
|
|
|
|
||||||
C0i = 1.922 × 10− 12 cm− 3 |
|
C0v = 8.638 × 10− 6 cm− 3 . |
|
|
||||||||
Характерные времена эволюции дефектов определяются обсуждавшимися выше механизмами и могут быть оценены (в секундах) как
T1 := 1 |
T1 = 4.075 × 10− 6 |
T2 := 1 |
+ |
1 |
. |
|
|||||
R Gv |
|
R Gv |
|
Kv |
|
Следовательно, временную эволюцию нужно отслеживать на интервале
tmin := 10− 10 s tmax := T2 T2 = 29.556 s ,
47
а диапазон изменения концентраций составляет от 10-15 до 10-6. На основании этого можно ожидать, что система уравнений будет обладать очень высокой степенью жесткости [5-6] и для ее решения следует использовать специальные методы.
Решение жесткой системы уравнений
Выполним замену независимой переменной.
|
t = τ0 exp(τ) |
|
|
τ0 := 10− 10 |
s , |
|
|||||||||
тогда диапазон ее изменения станет равным |
|
|
|
|
|
|
|
|
|
||||||
tmin |
|
τ1 = 0 |
|
tmax |
τ2 |
= 26.412 |
; |
||||||||
τ1 := ln τ0 |
|
τ2 := ln τ0 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
система уравнений принимает вид: |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
С |
|
|
G |
− R C |
|
C |
|
− Ki C |
|
|
|
|
|
|
d |
|
i |
= τ0 exp(τ) |
i |
|
v |
|
i |
|
|
i |
. |
|
|
|
|
|
− R C |
|
C |
|
− Kv C |
|
|
||||||
|
|
C |
|
G |
v |
i |
|
|
|
||||||
|
dτ |
v |
|
v |
|
|
|
|
|
v |
|
||||
Для решения жесткой системы уравнений воспользуемся встроенной функцией Stiffr(.). Для обращения к ней сформируем вектор f неизвестных, задаем начальные значения, определяем правую часть D(τ,f)
и формируем якобиан J(τ,f)
|
y0 |
( |
) |
Gi − R f f − Ki f |
|
( |
|
|
) |
|
|
|
|
||||
|
|
0 1 |
0 |
|
|
|
|
|
|
|
|||||||
f := z0 |
D |
τ,f |
:= Gv − R f |
f − Kv f |
exp |
τ |
|
τ0 |
|
|
|
||||||
|
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
( |
) |
|
Gi − R f f − Ki f |
−R f − Ki |
−R f |
|
|
|
( |
|
) |
|
|||||
|
0 1 |
0 |
1 |
|
−R f |
0 |
|
|
|
|
τ0 |
||||||
J |
τ,f := Gv − R f f − Kv f |
−R f |
|
− Kv |
exp |
τ |
|
||||||||||
|
|
|
0 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
Z := |
Stiffr(f,τ1 ,τ2 ,1000,D,J) |
i := 0 .. rows(Z) − 1 |
|
|
|
|
|
|
||||||||
Zt := Z 0 |
T := τ0 exp(Zt) |
|
Ci := Z 1 |
|
|
Cv := Z 2 . |
|||||||||||
Как видно из рис. 1, концентрации дефектов выравниваются и нарастают с одинаковой скоростью примерно до момента T1 – окончания первой фазы преимущественной рекомбинации дефектов между собой. Затем концентрация вакансий продолжает нарастать, а концентрация межузлий падает. В связи с большей подвижностью межузельные атомы быстрее, чем вакансии достигают стоков. К моменту T2 и вакансии достигают стоков, рост их концентрации замедляется и обе кривые подходят к найденным ранее стационарным решениям.
48
|
. |
4 |
|
|
|
|
|
|
|
|
|
|
|
1 10 |
5 |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
1 10 |
6 |
|
|
|
|
T1 |
|
|
|
|
T2 |
|
. |
|
|
|
|
|
|
|
|
|||
|
1 10 |
7 |
|
|
|
|
|
|
|
|
|
|
Ci |
. |
|
|
|
|
|
|
|
|
|
|
|
1 10 |
|
|
|
|
|
|
|
|
|
|
|
|
i |
. |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Cvi |
1 10 |
9 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||
|
1 10 |
10 |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
C0i 1 10 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
C0v |
1 10 |
12 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||
|
1 10 |
13 |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
1 10 |
14 |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
1 10 |
15 |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
1 10 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
0.01 0.1 1 10 100 |
||
|
|
1 .10 1 |
.101 .10 1 .101 .101 |
.101 .101 .10 |
|
|||||||
Ti
Рис. 1. Зависимость концентраций дефектов от времени
Оценка жесткости системы уравнений
В соответствии с рекомендациями [5-6] выполним линеаризацию системы уравнений. Выделяя малые отклонения в окрестности решения,
Ci(t) = Ci(to) + δCi(t) Cv(t) = Cv(to) + δCv(t)
находим d ( )
δCi(t) = −R Cv(to) δCi(t) + Ci(to) δCv(t) − Ki δCi(t)
dt
d δCv(t) = −R (Cv(to) δCi(t) + Ci(to) δCv(t)) − Kv δCv(t) dt
или, в матричной форме
δCi(t) Y(t) = δCv(t)
d Y(t) = A(t) Y(t) |
, |
где |
|
|||
dt |
|
|
|
|
|
|
−R Cv(to) − Ki |
−R Ci(to) |
|
||||
A(t) = |
−R C |
v |
(to) |
−R C |
(to) − K |
. |
|
|
|
i |
v |
||
Используя полученное выше решение, определяем матрицу А в каждой точке по времени и находим зависящие от времени ее собственные значения, используя встроенную функцию eigenvals(.).
49
|
|
|
|
|
|
|
|
|
|
|
−R Cv − Ki |
−R Ci |
|
|
||||
i := 0 .. rows(Ci) − 1 |
|
|
|
A := |
i |
|
|
|
i |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
i |
|
−R Cv |
|
−R Ci − Kv |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
i |
|
|
|
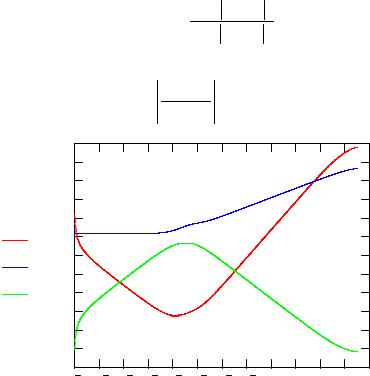
λ1i := eigenvals(Ai)0 |
|
|
|
|
λ2i := eigenvals(Ai)1 . |
|||||||||||||
Жесткость системы уравнений характеризуется соотношениями [5-6] |
||||||||||||||||||
|
|
|
|
Re(λk) < 0 |
и |
l |
= |
max( |
Re(λk) ) |
>> 1 . |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
min( Re(λk) ) |
|
|
|
|
|||
Определим индекс жесткости системы и проанализируем его зависи- |
||||||||||||||||||
мость от времени. |
|
|
Re(−λ1i) |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
S := |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
i |
Re(−λ2i) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
. |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 10 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 10 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 10 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 10 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Si |
|
1 10 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
− λ1 |
|
1 10 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
i |
1 10 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
− λ2i |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.01 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
0.01 0.1 |
1 |
10 |
100 |
|||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1 .10 1 .101 .10 1 .101 .10 1 .10 1 .101 .10 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ti |
|
|
|
|
|
|
|
Рис. 2. Зависимость собственных значений и индекса жесткости |
||||||||||||||||||
|
|
|
|
системы от времени |
|
|
|
|
|
|
|
|
|
|||||
Как видно из рис.2, все собственные значения действительные и отрицательные, а индекс жесткости системы изменяется в пределах девяти порядков. Это оправдывает применение в данной задаче специальной встроенной функции и соответствующего преобразования независимой переменной.
50
