
SimulationPhysProc_1_81
.pdf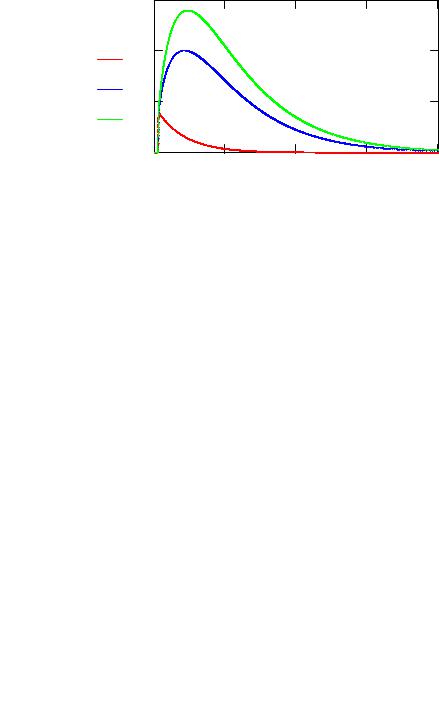
30 |
|
|
|
|
|
Nb 0 |
|
|
|
|
|
20 |
|
|
|
|
|
Nb 2 |
|
|
|
|
|
Nb 3 10 |
|
|
|
|
|
0 |
0 |
5 |
10 |
15 |
20 |
t
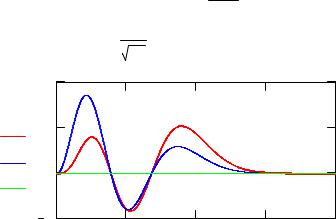
Рис. 1. Формирование импульса мощности реактора Nr(t) и лазерного блока Nb(t) во времени при коэффициенте связи krb = 0, 0.001, 0.0015
Из-за сильного отличия времён жизни нейтронов в реакторе и блоке динамика формирования импульсов в этих системах значительно различается. Из рис. 1 видно, что реакторный импульс формируется за доли мсек и имеет длительность по полувысоте такого же порядка,а импульс в лазерном блоке формируется в течение нескольких мсек и имеет длительность, в десятки раз превышающую длительность импульса в реакторе.
Упражнения
1. Используя символьный процессор MathCAD, получить стационарные решения системы уравнений для мощности и энергии реакторнолазерной системы. При заданных выше параметрах оценить полное энерговыделение в реакторе и активной среде лазерного блока.
2.Выполнить операцию обезразмеривания системы уравнений, принимая во внимание выбранные масштабы переменных.
3.Рассчитать зависимость от времени энерговыделения в реакторе и лазерном блоке. Сопоставить результат со стационарным решением.
4.Выполнить оценку жесткости полученной системы уравнений. Как зависит жесткость системы уравнений от коэффициента связи krb ?
5.Решить данную систему дифференциальных уравнений, используя встроенные функции Stiffr(.) или Stiffb(.). Насколько эффективнее применение методов решения жестких систем по сравнению с обычными методами?
6.Определить тип особых точек данной системы дифференциальных уравнений и проанализировать их устойчивость.
71
Глава 8. Стационарное уравнение Шредингера
Задача на собственные значения для оператора энергии в квантовой механике сводится к решению стационарного уравнения Шредингера
−h2 |
ΔΨ + V(r) Ψ = E Ψ . |
2 μ |
|
В одномерной задаче, когда Ψ(r) = R(r), а потенциальное поле зависит только от одной декартовой координаты, уравнение для связанных состояний с энергией Е имеет вид (см.[1,4])
2 |
|
|
|
|
|||
|
|
|
d |
R + k(r,E) |
2 R = 0 |
, |
|
|
|
|
2 |
|
|||
|
|
|
dr |
|
|
|
|
где граничные условия R( −∞) = R( ∞) = 0, а функция |
k(r,E)2 и условие |
||||||
нормировки заданы соотношениями |
|
⌠∞ |
|
||||
k(r,E)2 = |
2 μ |
(E − V(r)) , |
|
R(r)2 dr = 1 . |
|||
|
|
||||||
|
|
||||||
|
h2 |
|
⌡− ∞ |
|
|||
Если потенциальное поле V(r) , в котором находится частица, обладает осевой или сферической симметрией, получаемое после разделения переменных радиальное уравнение приводится к тому же виду. Для цилиндрических и сферических координат замена переменных и
функция k(r,E)2 |
соответственно равны |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
R(r) |
|
exp(i m φ) |
|
2 |
|
|
2 μ |
|
|
|
|
h |
2 |
|
|
2 |
|
|
|||||||
Ψ = |
|
k(r,E) |
= |
|
|
|
E − V(r) − |
|
|
(m − 0.25) |
||||||||||||||||
r |
|
2 π |
|
|
|
h |
2 |
|
|
|
|
|
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 μ r |
|
|
|||
|
R(r) |
|
|
|
|
|
|
|
|
|
|
2 μ |
|
|
|
|
h |
2 |
L (L + 1) |
|
||||||
Ψ = |
|
( |
θ,φ |
) |
k(r,E) |
2 |
= |
|
|
|
− |
|
. |
|||||||||||||
r |
|
|
|
|
|
2 |
|
|
|
|
2 |
|||||||||||||||
Y |
|
|
|
|
h |
|
E − V(r) |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 μ r |
|
||
Здесь μ – приведенная масса частиц, m и L – квантовые числа углового момента, Y(θ,φ) – соответствующая сферическая гармоника, используются однородные граничные условия R(0) = 0 и R( ∞) = 0, а условие
нормировки имеет вид |
∞ |
|
|
|
⌠ |
2 |
. |
||
|
|
|||
R(r) dr = 1 |
||||
⌡ |
|
|||
0 |
|
|
||
Будем считать, что функция V(r) обеспечивает существование связанных состояний (см.[1,4]), а волновая функция R(r) непрерывна и имеет нужное для алгоритма число непрерывных производных.
72
Метод Нумерова и метод стрельбы
Рассмотрим алгоритм численного решения - определение волновой функции R(r) и уровней энергии E, в предположении, что дифференциальная задача корректно поставлена и потенциал имеет не более одной (слева и справа) классических точек поворота. Будем искать решение задачи на конечном интервале [rmin , rmax], за пределами которого волновую функцию даже для высоко-возбужденных состояний можно считать равной нулю. Границы этого интервала являются параметрами расчета и должны уточняться в каждой конкретной ситуации. В сферическом и цилиндрическом случаях rmin будем полагать равным нулю. На этом интервале выберем равномерную сетку и выпишем трехточечную конечно - разностную аппроксимацию для второй производной волновой функции R
|
|
2 |
|
|
R |
n+1 |
− 2 R |
n |
+ R |
n−1 |
|
2 |
|
|
|
( |
4) . |
|
|
d |
|
|
= |
|
|
|
− |
r |
|
R |
IV |
+ |
|||||
|
|
2R |
|
|
|
|
|
|
|
|||||||||
|
|
|
r2 |
|
|
|
12 |
|
n |
O |
r |
|||||||
dr |
n |
|
|
|
|
|
|
|
|
|||||||||
Входящую сюда четвертую производную выразим с помощью дифференциального уравнения
(RIV) |
n |
= |
d2 |
|
(−k2 R) = |
− (k2 R)n+1 − 2 (k2 R)n + (k2 R)n−1 |
. |
|
|
||||||
|
|
dr2 |
2 |
|
|||
|
|
|
|
|
|
r |
|
Подставляя вторую производную в исходное уравнение и группируя слагаемые, получаем рекурентное соотношение, аппроксимирующее
исходное дифференциальное уравнение с точностью до |
r6. |
||||||
|
|
an−1 Rn−1 − cn Rn + bn+1 Rn+1 = 0 |
|
|
|
||
Коэффициенты рекурентного соотношения задаются формулами |
|||||||
an−1 = 1 + |
1 |
r2 (kn−1)2 |
|
bn+1 = 1 + |
1 |
|
r2 (kn+1)2 |
12 |
|
12 |
|||||
|
|
|
|
|
|||
|
|
cn = 2 1 − |
5 |
r2 (kn)2 . |
|
|
|
|
|
12 |
|
|
|
||
|
|
|
|
|
|
|
|
Отметим, что здесь функция k(rn,E) параметрически зависит от энергии.
Задавая значения функции в двух крайних точках сетки на левой границе, можно вычислить функцию во всех остальных точках и наоборот. Для решения задачи на собственные значения с однородными краевы-
73

ми условиями воспользуемся методом "встречной стрельбы", согласно которому (см. [3,5,6]) при "разумном выборе" энергии Е, с помощью полученного выше рекурентного соотношения, заданных нулевых значениях функции в крайних точках интервала и произвольных, но малых значениях в соседних с ними точках, можно вычислить функцию слева и справа до некоторой точки rc. В этой точке нужно выполнить условия непрерывности для функции и ее первой производной в соответствии с требованиями комплекса стандартных условий, налагаемых на волновую функцию (см.[1,2,4,8])
Rleft(rc) = Rright(rc) |
d Rleft(rc) = d Rright(rc) . |
|
|
dr |
dr |
Аппроксимация этих условий с помощью "разности назад" позволяет получить уравнение для определения неизвестных значений энергии Е, где знаменатель введен для масштабирования значений функции f(E)
f(E) = R(1rc) (Rright(rc − r) − Rleft(rc − r)) = 0 .
После решения этого уравнения и нахождения энергии Е следует вновь вычислить волновую функцию для найденного собственного значения. В качестве точки rc можно выбрать любую точку, например, из классически разрешенной области.
Выбор варианта "встречной стрельбы" объясняется тем, что решение в классически разрешенных областях является осциллирующим, тогда как в классически запрещенных областях оно содержит экспоненциальные вклады. При попытке счета в направлении вовнутрь классически запрещенной области одно из двух фундаментальных решений становится численно неустойчивым и приводит к появлению нефизического экспоненциально нарастающего решения (например, см. [3]).
Для потенциалов, имеющих более двух точек поворота, и, соответственно, три или более однородных решения, каждое из которых точно в своей области, общее решение должно сшиваться из нужного числа отдельных фрагментов.
Энергетические уровни чармония
В качестве примера решения задачи о собственных значениях для стационарного уравнения Шредингера выполним расчет уровней энергии двухкварковой системы (cм.[19]), открытой в 1974г. в экспериментах на электрон-позитронном коллайдере в Стенфорде и в продуктах реакции p+Be на протонном ускорителе в Брукхейвене и названной J/ψ - частицей. В спектре масс частице соответствовал резонанс с положением около 3.1 GeV и полушириной порядка 50 keV. Мезон J/ψ является одним из возбужденных состояний чармония.
74
Удовлетворительное описание уровней энергии чармония возможно в |
||||||||
рамках нерелятивистской потенциальной бесспиновой модели, согласно |
||||||||
которой ([20]) частица представляет собой состояние c c очарованного |
||||||||
(charm) кварка и антикварка, |
связанное посредством потенциала вида |
|||||||
α := 0.0967GeV fm |
β := 0.8615 |
GeV |
V(r) := |
−α + β r . |
||||
|
|
|
|
|
fm |
|
r |
|
Модельный потенциал строится так, чтобы на малых расстояниях он |
||||||||
практически имел бы кулоновскую форму, а на больших расстояниях |
||||||||
продолжал расти, обеспечивая невылетание (конфайнмент) свободных |
||||||||
кварков. |
Если выбрать массу кварка с и его антикварка равной |
|
||||||
mc2 := 1.35 |
GeV |
и |
hc := 0.19732858 |
GeV fm |
, |
|||
то потенциал взаимодействия кварков и функция k2(r,Е) принимают вид |
||||||||
U(r,L) := V(r) + |
hc2 L (L + 1) |
k2(r,E,L) := mc2 (E − U(r,L)). |
||||||
|
|
|
mc2 r2 |
|
|
hc2 |
|
|
|
|
|
|
|
|
State E, GeV <r>, fm |
||
|
|
|
|
|
|
1S |
0.364 |
0.407 |
U(r,0) |
2 |
|
|
|
|
1P |
0.772 |
0.663 |
|
|
|
|
1D |
1.060 |
0.868 |
||
|
|
|
|
|
|
|||
U(r,1) |
|
|
|
|
|
(усредненные по |
|
|
U(r,2) |
|
|
|
|
|
спину данные из [21]) |
||
|
|
|
|
|
Масса чармония |
|
||
0 |
|
|
|
|
|
|
||
0 |
|
|
|
|
M = 2 mc2 + E , |
|||
|
|
|
|
|
|
например, |
|
|
|
|
|
|
|
|
1.35 2 + 0.364 = 3.064 |
||
|
0 |
|
0.5 |
1 |
|
1.5 |
|
|
|
|
|
|
r |
|
|
|
|
Рис. 1. Потенциал взаимодействия, уровни энергии и средние |
|
|||||||
|
радиусы низших состояний чармония в S, P и D - волне |
|
||||||
Описанный выше алгоритм расчета значений волновой функции R(r) методом встречной стрельбы и значений функции f(E), получаемых на основе условий непрерывности, реализован в программе YNum(.).
Входные данные: a и b - границы области определения R(r), N- число интервалов разбиения, е - энергия, L - квантовое число полного момента, ε - параметр краевых условий стрельбы. Программа YNum(.) возвращает вектор значений R(r), в котором последний элемент - значение f(E).
75

YNum(N,a,b ,e,L,ε) := r ← |
b − a |
|
|
|
||||||
|
N |
|
|
|||||||
|
|
|
|
|
|
|
||||
2 ← |
|
r2 |
|
|
|
|||||
12 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
Nc ← floor(0.2 N) |
||||||||||
Y0 ← 0 |
|
|
||||||||
Y1 ← ε |
|
|
||||||||
ka ← |
|
2 k2(a,e,L) |
||||||||
kc ← 2 k2(a + r,e,L) |
||||||||||
for n 1 .. Nc |
|
|
||||||||
|
|
|
α ← 1 + ka |
|
|
|||||
|
|
|
|
|||||||
|
|
|
γ ← 2 − 10 kc |
|||||||
|
|
|
kb ← 2 k2 a + r (n + 1) ,e,L |
|||||||
|
|
|
Yn+1 ← |
γ Yn − α Yn−1 |
|
|||||
|
|
|
|
1 + kb |
||||||
|
|
|
ka ← kc |
|
|
|||||
|
|
|
kc ← kb |
|
|
|||||
yn0 ← YNc |
|
|
||||||||
yn1 ← YNc+1 |
|
|
||||||||
YN ← 0 |
|
|
||||||||
YN−1 ← ε
kb ← 2 k2(b ,e,L)
kc ← 2 k2(b − r,e,L)
for n N − 1 ,N − 2 .. Nc + 1

 ka ← 2 k2 a + r (n − 1) ,e,L
ka ← 2 k2 a + r (n − 1) ,e,L
β ← 1 + kb
76
γ ← 2 − 10 kc
Yn−1 ← |
γ Yn − β Yn+1 |
1 + ka |
kb ← kc kc ← ka
const ← yn1 (YNc+1)− 1 for n Nc .. N
Yn ← Yn const Ym ← max(Y)
|
|
|
YN+1 ← (yn0 − YNc)Ym− 1 |
|
|||
|
|
|
Y |
|
|
|
|
Выполним отделение корней. Из графика потенциала ясно, что в P и D- |
|||||||
волнах могут быть уровни только с положительной энергией, тогда как |
|||||||
в S - волне следует просматривать и отрицательные энергии. Пусть |
|||||||
N := 2000 |
|
a := 0.0001 |
b := 5.0 |
L := 2 |
ε1 := 10− 6 |
||
E := −0.2,−0.19 .. 3.0 |
f(E) := YNum(N,a,b ,E,L,ε1)N+1 |
||||||
f(E) |
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
2 |
|
3 |
|
|
|
E |
|
|
|
|
|
|
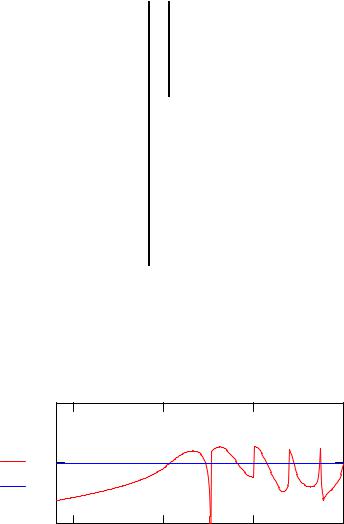
Рис. 2. К оценке положения корней функции f(E) |
|
||||
Анализируя график функции f(E), выберем начальное приближение |
|||||||
для корня и уточним его с помощью встроенной функции root(.). |
|||||||
TOL := 10− 6 |
E := 1.8 |
e0 := root(f(E) ,E) |
e0 = 1.818 |
GeV |
|||
|
|
|
77 |
|
|
|
|
Для найденного значения энергии e0 выполняем окончательный расчет волновой функции, нормируем и строим графики функций R и ψ = R/r.
R := YNum(N,a,b ,e0,L,ε1) |
r := |
b − a |
A2 := r ∑R |
2 |
||||
N |
|
|||||||
i := 1 .. N |
R |
:= R |
1 |
r := a + i r |
ψi := R |
1 |
|
|
|
i |
i |
A2 |
i |
|
i |
r |
|
|
|
|
|
|
|
|
i |
|
|
2 |
|
|
|
|
|
|
|
Ri |
1 |
|
|
|
|
|
|
|
ψi |
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
1 0 |
|
1 |
2 |
|
3 |
4 |
|
ri
Рис. 3. Радиальная волновая функция 3D-состояния чармония
Как видно из рис. 2, на графике функции f(E) имеются нерегулярности, например, в точках Е = 1.54 , 2.02 и т.д. Эти точки не соответствуют физически реализуемым состояниям и являются побочными эффектами расчета. В этом легко убедиться, проверяя, удовлетворяет ли найденная волновая функция для последовательных состояний требованиям теоремы о нулях (см. [1,4]).
Упражнения
1. Построить расчетную формулу метода НумероваКаулинга для не-
однородного уравнения вида R(r)'' + k(r,E)2 R(r) = S(r) .
2. Используя предложенную программу расчета, проанализировать зависимость значений волновой функции от входных данных задачи и параметра TOL. Правильно ли они выбраны для рассчитываемого 3Dсостояния? Как их можно изменить при расчете S и P-состояний?
3. Вычислить и составить таблицу уровней энергии и средних значений радиуса чармония, используя предложенную программу расчета. Удовлетворяют ли найденные волновые функции теореме о нулях? Вероятность аннигиляции кварка и антикварка (см. [20,21]) пропорцио-
78
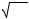
нальна квадрату модуля волновой функции в нуле |ψ(0)|2. Вычислить
еедля найденных волновых функций. Как она зависит от шага сетки?
5.Найти уровни энергии и волновые функции атома водорода и позитрония – связанного состояния электрона и позитрона; сравнить с [1,4].
6.Мезон боттомоний представляет собой связанное состояние b b
прелестного (beauty) кварка и его антикварка [20]. Пусть масса b-кварка равна mb= 4.77 GeV, а параметры потенциала α, β остаются прежними. Рассчитать и составить таблицу уровней энергии и средних значений радиуса боттомония, используя предложенную программу расчета. Удовлетворяют ли найденные волновые функции теореме о нулях?
7. Рассчитать уровни энергии и волновые функции частицы, движущейся в однородном гравитационном поле над поверхностью земли и упруго отражающейся от нее. Полученные результаты сопоставить с точным решением (см. [2]). Потенциал и граничные условия задачи имеют вид:
0 < x < ∞ V(x) = if (x < 0 ,∞,m g x) Ψ(0) = 0 Ψ(∞) = 0 .
8. Найти энергии и волновые функции состояний в полях (см. [1,2,4]):
а) V(x) =α |x| ; б) V(x) = –Vo/cosh(x/a)2; в) V(x)= Vo (a/x – x/a)2, (x>0);
г) потенциале Морса и (6-12) с параметрами молекулы Н2 (см. гл.1);
д) потенциала Хюльтена V(r) = – V0exp(–r/a)/(1–exp(–r/a)), при L = 0; е) потенциала Кратцера V(r) = – 2D (a/r – a2/(2r2)) , при L ≥ 0 .
9. Вычислить уровни энергии и волновые функции состояний электрона
в квантовых системах (GaAs, mef = 0.067me , внешнее поле ε = 1meV/A)
а) яма с V(x) = if (x < 0 ,0 ,if (x > a,−a ε,−Vo − x ε)), а=100А, Vо=1eV;
б) треугольная яма с полемV(x) = if (x < 0 ,∞,ε x); в) квантовое кольцо с V(r)= a/r2 +br2 –Vo, a= 9.1 108 meVA2, b= 2.2 10-7 meVA-2, Vo=2 a b.
10. Рассчитать одночастичные уровни энергии и волновые функции
нейтронов и протонов в ядре |
208Pb в потенциале Вудса - Саксона и |
||||||||||||||||||
кулоновском поле с параметрами (см. [22]) |
|
|
|
|
|
|
|
|
|||||||||||
|
|
r − R − 1 |
Von = 45.7 |
|
и |
Vop = 57.9 |
MeV |
||||||||||||
V(r) = −Vo 1 |
+ exp |
|
|
, |
e2 = 1.4409 |
MeV fm |
Z = 81 |
||||||||||||
a |
|||||||||||||||||||
|
|
(Z − 1) e2 (Z − 1) e2 |
|
|
r |
|
2 |
, R = 7.58 |
fm |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− R |
|
a = 0.65 |
|
||||||
Vc(r) = if r > |
R, |
|
r |
, |
|
2 R |
|
|
|
3 |
|
fm |
|||||||
11. Как изменятся результаты в предыдущей задаче с учетом спинорбитального взаимодействия? (Результаты можно сопоставить с [23]).
79
Литература
1.Давыдов А.С. Квантовая механика. М.: Наука, 1973.
2.Флюгге З. Задачи по квантовой механике. т.1-2, М.: МИР, 1974.
3.Koonin S.E., Meredith D.C. Computational Physics. Addison-Wesley Pub. Company, CalTech, 1985.
4.Мессиа А. Квантовая механика. М.: Наука, т.1,2, 1978.
5.Калиткин Н.Н. Численные методы. -М.: Наука, 1976, -480с.
6.Пирумов У.Г. Численные методы.-М.: Дрофа, 2003, -224с.
7.Физические величины. Справочник. Под редакцией
И.С.Григорьева, Е.З.Мейлихова. М., Энергоатомиздат, 1991.
8.Матвеев А.Н. Атомная физика. -М.: Высш. шк., 1989, -439с.
9.Мотт Н., Месси Г. Теория атомных столкновений. -М.: Мир., 1969.
10.Ландау Л.Д., Лифшиц Е.М. Механика. -М.: Наука, 1988.
11.Экштайн В. Компьютерное моделирование взаимодействия частиц с поверхностью твердого тела. -М.: МИР, 1995, -321с.
12.Машкова Е.С., Молчанов В.А. Применение рассеяния ионов для анализа твердых тел. -М.: Энергоатомиздат, 1995, -176с.
13.Минкин В.И., Симкин Б.Я., Миняев Р.М. Теория строения молекул. Ростов-на-Дону, "Феникс", 1997, -560с.
14.Steinfeld J.I. et .al. Chemical Kinetics and Dynamics. Prentice Hall, 1999, p.179-216.
15.Печенкин В.А. Период нестационарности концентраций точечных дефектов в теории распухания металлов. ЖТФ т.52, в.9, с.1712-20 (1982)
16.Mansur L.K. Void swelling in metals and alloys under irradiation: an assessment of the theory. Nuclear Technology v.40, p. 5-34, 1978.
17.Карлов Н.В. Лекции по квантовой электронике. -М.: Наука, 1988.
18.Хакен Г. Лазерная светодинамика. -М.: Мир, 1988, -350с.
19.Готтфрид К., Вайскопф В. Концепции физики элементарных
частиц. -М.: МИР. 1988.
20.Быков А.А., Дремин И.М., Леонидов А.В. Потенциальные модели кваркония. УФН, т. 143, в. 1, с. 3-32 (1984).
21.Miller K.J. and Olsson M.G.. Phys. Rev. D25, (1982), p.2382; Durand L. et.al. Phys. Rev. D28, (1983), p.607.
22.Широков Ю.М, Юдин Н.П.. Ядерная физика. -М.: Наука,1980,-728с.
23.Михайлов В.М., Крафт О.Е. Ядерная физика. Изд-во ЛГУ,1988,328с.
80
