
SimulationPhysProc_1_81
.pdf
|
Рассеяние на потенциале Ленарда-Джонса |
|
|
||||||
Рассчитаем зависимость угла отклонения от прицельного параметра |
|||||||||
для потенциала с параметрами взаимодействия атомов неона |
|
|
|||||||
|
a := 2.74 A |
Vo := 0.0031 |
|
eV |
|
|
|
||
|
|
a 12 |
a 6 |
|
|
|
|
||
|
|
|
|
|
. |
|
|
|
|
|
V(r) := 4 Vo r |
− r |
|
|
|
|
|||
Выберем энергию частицы E порядка глубины потенциальной ямы Vo, |
|||||||||
определим функцию f(r,b,E) |
и проанализируем зависимость r_min |
от |
|||||||
прицельного параметра. |
|
|
|
|
2 |
|
|
|
|
|
E := 0.8 Vo |
f(r,b ,E) := |
1 − |
b |
|
V(r) |
|
|
|
|
r |
|
− |
E |
|
|
|||
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
f(r,2,E) |
1 |
|
|
|
|
|
|
|
|
f(r,3,E) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(r,4,E) |
|
|
|
|
|
|
|
|
|
f(r,4.8,E) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(r,6,E) |
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
4 |
6 |
|
|
|
8 |
10 |
|
|
|
|
r |
|
|
|
|
|
|
|
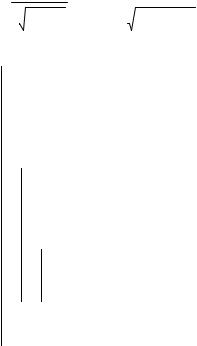
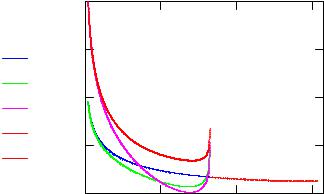
Рис.2 . К расчету расстояния наибольшего сближения |
|
|||||||
Как видно из рис.2, при выбранной энергии для большинства значений прицельного параметра b из интервала [2,6] существует единственное решение r_min(b,E). Однако при b = 4.8 функция f(r,b,E) принимает очень малые значения в широком интервале изменения r. Это приводит
кнеоднозначности в определении расстояния наибольшего сближения
илогарифмической расходимости интеграла (см.[3,9]). Физическая причина этого явления в том, что частица движется по спирали, асимптотически приближаясь к минимальному радиусу, – происходит рассеяние
по спирали и угол отклонения Θ становится многозначной функцией.
11
Для решения нелинейного уравнения и нахождения r_min(b,E) воспользуемся методом Ньютона (см. [5,6]). Определим реализующую его подпрограмму Rn(.) и функцию Th(.) для расчета угла отклонения.
Rn(f,df ,Rold,eps,e,b) := |
|
Rnew ← Rold − |
f(Rold,b ,e) |
|
|
||||||||||||
df (Rold,b ,e) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
while |
|
Rnew − Rold |
|
|
> eps |
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
Rold ← Rnew |
|
|
f(Rold,b ,e) |
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
Rnew ← Rold − |
|
|
|||||||||
|
|
|
|
|
df (Rold,b ,e) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
Rnew |
|
|
|
|
|
|
|
|
|
|
||
df (r,b ,E) := |
d f(r,b ,E) |
|
|
|
TOL := 10− 6 |
||||||||||||
|
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
⌠d |
1 |
|
|
⌠d |
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Th(E,b ,c,d) := 2 b |
|
|
|
|
|
|
dr − |
|
|
|
|
|
|
dr |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
r |
r2 − b2 |
|
r |
r2 f(r,b ,E) |
|
|
||||||||
|
|
⌡ |
|
|
|
|
|
⌡ |
|
|
|
|
|
|
|
||
|
|
b |
|
|
|
|
|
c |
|
|
|
|
|
|
|
||
Tt(ee ,J,db,n ,rm) := |
|
b0 ← 0.1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
for |
|
i 1 .. n |
|
|
|
|
|
|
|
|||||
bi ← bi−1 + db for j 0 .. J
rn ← Rn(f,df ,b0,TOL,ee j,b0) θ0, j ← Th(ee j,b0,rn,rm)
for i 1 .. n
rn ← Rn(f,df ,rn,TOL,ee j,bi)
θi, j ← Th(ee j,bi,rn,rm) zz ← augment(b ,θ)
zz
12
Для потенциала Ленарда-Джонса в качестве оценки r_max можно вы- |
||||
брать величину порядка (4 ÷5)a, |
где a – параметр потенциала. Рассчи- |
|||
таем зависимость угла отклонения Θ от прицельного параметра b для |
||||
разных значений энергии E налетающей частицы. |
||||
E := ( 50 Vo |
5 Vo 1.5 Vo Vo |
0.8 Vo )T |
Θt := Tt(E,4 ,0.01,700 ,4 a) |
|
|
|
b := Θt 0 |
Θ := submatrix(Θt,0 ,700 ,1 ,5) |
|
|
4 |
|
|
π |
|
|
|
|
|
Θ 0 |
2 |
|
|
|
Θ 1 |
|
|
|
|
Θ 2 |
0 |
|
|
|
Θ 3 |
2 |
|
|
|
Θ 4 |
|
|
− π |
|
|
|
|
||
|
4 |
|
|
|
|
0 |
2 |
4 |
6 |
|
|
|
b |
|
|
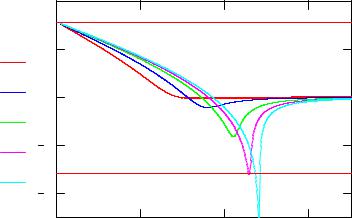
Рис. 3. Зависимость угла отклонения от прицельного |
|||
|
|
параметра для потенциала Ленарда-Джонса |
||
Как и следовало ожидать, угол отклонения Θ при малых значениях прицельного параметра b близок к π, а при больших прицельных параметрах стремится к нулю для любой энергии частицы. При энергии E ≈ Vo и прицельных параметрах, сравнимых с характерным прост-
ранственным масштабом потенциалаb ≥ a , появляются отрицательные
значения угла отклонения, а в самой зависимости Θ(b) наблюдаются минимумы, с уменьшением энергии уходящие в −∞ вследствие рас-
сеяния по спирали. Отметим, что при энергии E = 0.8Vo сингулярным является значение прицельного параметра b, близкое к 4.8, в соответствии с проведенным выше анализом зависимости функции f(r,b,E) от переменных r и b (см. рис. 2).
13
|
|
Расчет дифференциального сечения |
|
||||||
Зная зависимость угла отклонения от прицельного параметра для |
|||||||||
разных значений энергии налетающей частицы, можно рассчитать |
|||||||||
угловую зависимость дифференциального сечения – экспериментально |
|||||||||
наблюдаемой величины. По определению сечения (см.[3,8,10]) |
|||||||||
|
|
dσ |
= |
b(Θ) |
db |
|
|
||
|
|
|
( |
Θ |
) |
dΘ |
|
|
|
|
|
dΩ |
sin |
|
|
|
|||
Сначала рассчитаем сечение как функцию прицельного параметра. |
|||||||||
Для этого проведем сплайновую интерполяцию (см.[5,6]) |
зависимости |
||||||||
угла отклонения от прицельного параметра и выполним дифференци- |
|||||||||
рование сплайна. В качестве примера выберем |
вариант с E = 1.5Vo |
||||||||
и вычислим сечение в тех же узлах сетки, где задана зависимость Θ(b). |
|||||||||
|
Dx(q ,bb,Vs,x) := d |
interp(Vs,bb,q ,x) |
|
||||||
|
|
|
|
dx |
|
|
|
|
|
|
F(q ,bb) := Vs ← cspline(bb,q) |
|
|
||||||
|
|
n ← rows(q) |
|
|
|
||||
|
|
|
for |
i 0 .. n − 1 |
|
|
|||
|
|
|
dsi ← |
|
|
bbi |
|
||
|
|
|
|
sin(qi)Dx(q ,bb,Vs,bbi) |
|||||
|
|
|
|
|
|
||||
|
|
ds |
|
|
|
|
|
|
|
N := rows(Θ) − 1 |
|
Θ := Θ 2 |
dS := F(Θ,b) |
||||||
. |
5 |
|
|
|
|
|
|
|
|
1 10 |
|
|
|
|
|
|
|
|
|
. |
4 |
|
|
|
|
|
|
|
|
1 10 |
|
|
|
|
|
|
|
|
|
. |
3 |
|
|
|
|
|
|
|
|
1 10 |
|
|
|
|
|
|
|
|
|
dS |
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
1 0 |
1 |
|
2 |
|
3 |
4 |
5 |
6 |
|
|
|
|
|
|
b |
|
|
|
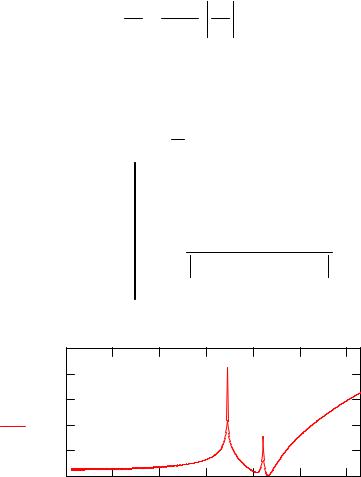
Рис. 4. Зависимость дифференциального сечения от прицельного |
|||||||||
параметра для потенциала Ленарда-Джонса при E = 1.5Vo |
|||||||||
14
Неограниченный рост сечения при больших прицельных параметрах связан с неограниченным радиусом действия потенциала. При этом не только угол отклонения, но и его производная стремятся к нулю.
Острый пик при b ~ 3.4 соответствует стремлению угла отклонения к нулю при промежуточных значениях прицельного параметра и отражает эффект "сияния вперед". Пик в сечении около значения b ~ 4.2 связан с обращением в нуль производной угла отклонения как функции прицельного параметра (см. рис.3) и соответствует так называемому "радужному рассеянию" (см.[9]) . При меньшей энергии этот эффект может трансформироваться в рассеяние по спирали (см. рис.3).
Если угол отклонения Θ выходит за пределы интервала [0,π] экспериментально наблюдаемых углов рассеяния, то в соотношении для сечения его необходимо привести к указанному интервалу и выполнить суммирование по всем ветвям многозначной функции b(Θ).
При расчете сечения ограничимся областью сравнительно высоких энергий так, чтобы угол отклонения по модулю не превосходил значения π. Как видно из рис. 3, в этом случае необходимо учитывать три ветви многозначной функции, соответствующей интервалам измене-
ния прицельного параметра [0,b(θ=0)], [b(θ=0),b(θmin)] и [b(θmin),bmax].
Сначала оценим, а затем рассчитаем границы этих интервалов. Ans := "Deflection angle < -3.14"
bounds(q ,bb,n) := |
θn ← min(q) |
||
|
if θn < −π |
||
|
|
|
return Ans |
|
|
|
|
|
|
|
break |
|
for |
i 0 .. n − 1 |
|
|
|
|
i0 ← i if qi qi+1 < 0 |
|
|
|
|
|
|
|
i1 ← i if qi = θn |
|
i0 |
|
|
|
|
|
|
|
i1 |
|
|
Vs := cspline(b ,Θ) f0(x) := interp(Vs,b ,Θ,x) |
df0(x) := |
d |
f0(x) |
||||
|
|||||||
io := bounds(Θ,b ,N)0 |
|
|
|
|
|
dx |
|
x := b |
io |
b0 := root(f0(x) ,x) |
b0 = 3.43 |
||||
|
|
|
|
|
|
|
|
15

i1 := bounds(Θ,b ,N)1 x := b |
i1 |
b1 := root(df0(x) ,x) |
b1 = 4.192 |
|
|
|
|
|
|
θn := −ΘN |
θn = 0.027 |
|
θmin := f0(b1) |
θmin = −1.636 |
θmax := Θ0 |
θmax = 3.068 |
|
|
|
Для построения зависимости сечения от угла рассеяния необходимо привести углы отклонения к интервалу [0,π], симметрично отразив область отрицательных углов и выполнив их упорядочивание в порядке возрастания. При этом сечения на каждой из трех ветвей оказываются найденными в разных узловых точках и для их суммирования необходима предварительная интерполяция сечений по соответствующим массивам углов. Для выполнения этих операций могут быть использованы следующие три функции. Следует отметить, что вблизи границ интервалов углов погрешность интерполяции заметно возрастает.
f1(q ,ds ,n ,i0,x) := a ← submatrix(q ,0 ,i0,0 ,0)
b← submatrix(ds ,0 ,i0,0 ,0)
c← augment(a,b)
c ← csort(c,0)
Vs ← cspline(c 0 ,c 1 )
z ← interp(Vs,c 0 ,c 1 ,x)
f2(q ,ds ,n ,i0,i1,x) := a ← −submatrix(q ,i0 + 2 ,i1 − 1 ,0 ,0) b ← submatrix(ds ,i0 + 2 ,i1 − 1 ,0 ,0) Vs ← cspline(a,b)
z ← interp(Vs,a,b ,x)
f3(q ,ds ,n ,i1,x) := a ← −submatrix(q ,i1 + 1 ,n ,0 ,0)
b← submatrix(ds ,i1 + 1 ,n ,0 ,0)
c← augment(a,b)
c ← csort(c,0)
Vs ← cspline(c 0 ,c 1 )
z ← interp(Vs,c 0 ,c 1 ,x)
Сечения на каждой ветви в зависимости от угла рассеяния и их сумма показаны на рис. 5. Как и следовало ожидать, сечения на второй и
16
третьей ветви имеют особенность при θ = –θmin , отвечающую "радуж- |
||||
ному рассеянию". Эту же особенность имеет и суммарное сечение. |
||||
ds1(θ) := f1(Θ,dS,N,io,θ) |
|
ds2(θ) := f2(Θ,dS,N,io,i1,θ) |
||
ds3(θ) := f3(Θ,dS,N,i1,θ) |
|
dsdΩ(θ) := ds1(θ) + ds2(θ) + ds3(θ) |
||
θ := θn ,θn + 0.001 .. −θmin |
|
θ1 := −θmin,−θmin + 0.01 .. θmax |
||
1 .104 |
|
|
|
|
ds1(θ) 1 .103 |
|
|
|
|
ds2(θ) |
|
|
|
|
ds3(θ) |
100 |
|
|
|
|
|
|
|
|
ds1(θ1) |
|
|
|
|
dsdΩ(θ) |
10 |
|
|
|
|
1 0 |
1 |
2 |
3 |
|
|
|
θ,θ,θ,θ1,θ |
|
Рис. 5. Зависимость дифференциального сечения от угла рассеяния для потенциала Ленарда-Джонса при E = 1.5Vo
Упражнения
1.Для потенциала Ленарда-Джонса рассчитайте расстояния наибольшего сближения частицы и силового центра как функцию прицельного параметра и энергии. Постройте контурный график функции rmin(E,b).
2.Опишите характер сингулярности сечения (зависимость сечения от угла) при "сиянии", "радужном рассеянии" и рассеянии по спирали для потенциала Ленарда-Джонса (см. [9]).
3.Одна из кривых зависимости угла отклонения от прицельного параметра , приведенная на рис. 3 при E = Vo, имеет значения углов < - π, соответствующие эффекту "сияния назад". Рассчитайте в этом случае зависимость сечения от угла, учитывая вклад от пяти ветвей многознач-
ной функции b(Θ).
4. Для потенциала Ленарда-Джонса при используемых выше значениях параметров и энергии E = 0.8Vo показать, что "рассеяние по спирали" соответствует такому прицельному параметру b0 , при котором кривая
f0(r) = 1 - b2/r2 "касается и скользит" вдоль кривой зависимости V(r)/E.
17
5. Рассчитайте связь угла рассеяния и прицельного параметра для a) потенциала твердых сфер U(r) = 0 при r > R и U(r) = ∞ при r ≤ R ,
где R –сумма радиусов сфер; |
b) потенциала вида |
|
V(r) = α r− n , |
n ≥ 1 , |
α > 0 . |
Постройте зависимость дифференциального сечения от угла рассеяния. Сравните результаты с аналитическим решением при n = 1 (формула Резерфорда) и n = 2 (см. [9,10]). Как изменятся результаты при α < 0 ?
6. Рассчитайте связь угла рассеяния и прицельного параметра в потен-
циале Морса с параметрами rmin = 0.741 A, β = 2 1/A, Vо = 4.747 eV V(r) = Vo 1 − exp −β (r − rmin) 2 − 1 .
При энергии E ~ Vo оцените критическое значение прицельного параметра, при котором происходит переход в режим рассеяния по спирали. Постройте зависимость дифференциального сечения от угла рассеяния, ограничиваясь диапазоном энергий, при которых |Θ| < π.
7. Для потенциала Кратцера рассчитайте связь угла рассеяния и прицельного параметра и постройте зависимость дифференциального сече-
ния от угла рассеяния |
|
|
|
|
||||
V(r) = −Vo |
a |
|
|
|
a |
, где a = 0.74166 A, Vo= 4.747 eV. |
||
|
|
|
2 |
− |
|
|
||
r |
|
r |
||||||
8. При расчете угла отклонения Θ возникают трудности из-за сингулярности подынтегральной функции при r = rmin и бесконечного верхнего
предела интегрирования. Заменой |
|
x = rmin/r |
|
преобразуем формулу к |
||||||||||||
виду |
|
|
|
|
⌠ |
1 |
|
|
|
|
|
|
|
|
− 0.5 |
|
|
|
2 b |
|
|
|
|
|
|
V(x) |
|
b |
2 |
x |
2 |
|
|
Θ |
= π − |
|
|
|
1 |
− |
− |
|
|
|
dx . |
|||||
rmin |
|
|
E |
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
⌡ |
|
|
|
|
|
rmin |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0
Для потенциала Ленарда-Джонса
a)найти Θ(E,b), вычисляя интеграл методом Гаусса-Кристофеля [4,5];
b)найти Θ(E,b) и эффективный порядок точности в процессе Эйткена;
с) показать, что в методе средних структура остаточного члена квадратурной формулы определяется сингулярностью и имеет вид
R = a1 h0.5 + a2 h1.5 + a3 h2 + O(h2.5) ;
d) выделяя особенность c учетом первых двух слагаемых и уточняя расчет по трем вложенных сеткам, методом средних вычислить Θ(E,b).
18
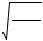
Глава 3. Расчет и построение траекторий
Построение траекторий частиц является очень распространенной задачей, требующей применения дифференциальных уравнений. Как обычно такая задача формулируется как задача Коши в форме уравнений Ньютона или Гамильтона. Рассмотрим несколько примеров задач, связанных с необходимостью расчета траекторий.
Кулоновский потенциал
Рассмотрим классическую задачу о рассеянии α–частиц на ядрах Au, изучавшуюся в опытах Гейгера и Марсдена. В силу большой разницы в массах будем считать ядро золота неподвижным так, что α– частица рассеивается на силовом центре с кулоновским потенциалом. Пусть энергия α–частицы во входном канале равна 5 MeV.
q := 4.8 10− 10 |
CGSu |
U(r) = q1 q2 |
aem := 1.67 10− 24 g |
|
|
r |
|
q1 := 2 q |
|
q2 := 79 q |
mα := 4 aem g |
Tα := 5 106 eV |
Tα := Tα 1.6 10− 12 |
Tα = 8 × 10− 6 erg |
|
Оценим начальную скорость и расстояние наибольшего сближения при лобовом столкновении.
Vz0 := 2 Tα |
Vz0 = 1.548 × 109 |
cm |
mα |
|
s |
Rc := q1 q2 Tα− 1 |
Rc = 4.55 × 10− 12 |
cm |
Используем эти оценки для выбора начального положения частицы и диапазона изменения прицельного параметра столкновения.
zmin := −4 10− 11 cm |
zmax := 5 10− 11 |
cm |
bmin := 5 10− 13 cm |
bmax := 4.0 10− 12 |
cm |
Для кулоновского потенциала задача имеет аналитическое решение (см. упр. 1). Если частица налетает на рассеивающий центр вдоль оси Z из области отрицательных значений z с прицельным параметром b и в полярных координатах угол θ отсчитывается от оси Z в направлении против часовой стрелки, то уравнение траектории имеет вид:
r(θ) = |
2 b2 |
2 b sin(θ) − Rc (1 + cos(θ)) |
19
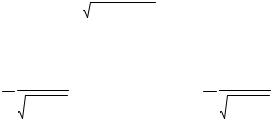
Семейство траекторий имеет огибающую вида
Yp(z) := 2 Rc (z + Rc) .
Переопределим потенциал U и проекции силы Fz и Fy как функцию переменных z и y и выпишем уравнения движения в форме Ньютона.
d |
q1 q2 |
|
|
d |
q1 q2 |
|
|
||||
Fz(z,y) := − dz |
z |
2 |
+ y |
2 |
|
Fy(z,y) := − dy |
z |
2 |
+ y |
2 |
|
|
|
|
|
|
|
|
|
||||
Задаем начальные условия для координат и скоростей и определим правую часть системы уравнений в форме, предполагаемой при использовании встроенных функций Rkadapt(.) или Radau(.). Построим семейство из N = 5 траекторий.
a := 4 10− 10 cm b := 5 10− 13 cm n := 0 .. 4
|
z0 |
|
|
|
|
|
|
|
−a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vz0 |
|
|
структура вектора неизвестных |
f := |
|
Vz0 |
|
|
|
||||
|
|
|
|
и их начальные значения |
|
n |
|
|
|
|
|
||
|
y0 |
|
|
|
|
|
|
b (1 + 7 n) |
|
||||
Vy0 |
|
|
|
|
|
|
0 |
|
|
|
|||
d z = Vz |
|
|
|
|
|
|
f1 |
|
|
|
|||
dt |
|
|
|
|
структура |
|
|
1 |
|
|
|
|
|
d |
Vz = Fz(z,y) |
|
|
|
Fz(f0,f2) |
|
|||||||
системы |
|
|
|
|
|
||||||||
|
mα |
||||||||||||
dt |
|
|
|
mα |
уравнений и |
D(t,f) := |
|
|
f |
|
|
|
|
d |
|
|
|
|
определение ее |
|
|
|
|
|
|
|
|
y = Vy |
|
правой части |
|
|
|
3 |
|
|
|||||
dt |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Fy(z,y) |
|
|
|
|
Fy(f ,f |
) |
||||
d |
Vy = |
|
|
|
|
||||||||
|
mα |
|
|
mα |
0 |
2 |
|
||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценим время расчета каждой траектории по порядку величины как время, необходимое для пересечения области размером 2a со скоростью Vz0. Поскольку численные значения времени малы (< 10 -15), то чтобы их распечатать, надо изменить максимальный диапазон выводимых на экран (но не рассчитываемых!) чисел в меню Format-> Result-> Tolerance->Zero threshold (15) ,например, на 30.
time := |
2 a |
time = 5.169 × 10− 19 sec |
|
Vz0 |
|||
|
|
20
