
SimulationPhysProc_1_81
.pdfПроанализируем структуру полученного решения. |
{201,5} |
|
|
|
|||
|
|
{201,5} |
|
Xn := Rkadapt(fn,0 ,time,200,D) |
|
|
|
X = |
{201,5} |
||
|
|
{201,5} |
|
|
|
|
|
|
{201,5} |
|
|
Каждая строка во вложенном (nested) массиве соответствует одной траектории. Извлечем, например, данные для первой траектории. Как видно, столбцы содержат информацию в следующем порядке: время, z – координата, скорость Vz, y – координата, скорость Vy. Данные можно просмотреть, используя линейку листания.
|
|
0 |
1 |
2 |
|
0 |
0 |
-4·10 -10 |
1.548·109 |
|
1 |
2.585·10 -21 |
-3.96·10 -10 |
1.548·109 |
|
2 |
5.169·10 -21 |
-3.92·10 -10 |
1.547·109 |
X = |
3 |
7.754·10 -21 |
-3.88·10 -10 |
1.547·109 |
0 |
4 |
1.034·10 -20 |
-3.84·10 -10 |
1.547·109 |
|
||||
|
5 |
1.292·10 -20 |
-3.8·10 -10 |
1.547·109 |
|
6 |
1.551·10 -20 |
-3.76·10 -10 |
1.547·109 |
|
7 |
1.809·10 -20 |
-3.72·10 -10 |
1.547·109 |
|
8 |
2.068·10 -20 |
-3.68·10 -10 |
1.547·109 |
Для построения графика извлечем z и y – координаты всех траекторий и разместим их в едином массиве.
Z := augment (X0)1 ,(X1)1 ,(X2)1 ,(X3)1 ,(X4)1 Y := augment (X0)3 ,(X1)3 ,(X2)3 ,(X3)3 ,(X4)3
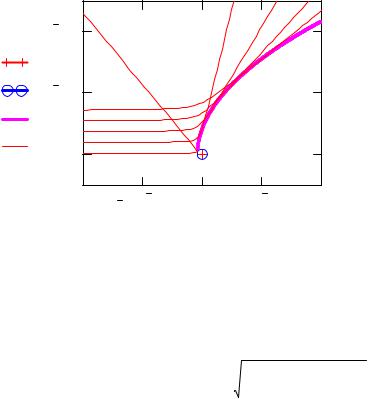
Как видно из рис. 1, все траектории имеют ожидаемое поведение и каждая из них касается огибающей, не пересекая ее.
Важным показателем качества полученного решения является точность сохранения энергии частицы в процессе расчета. Ясно, что наиболее "жесткими" являются условия, в которых частица движется по первой траектории (n = 0). Эта траектория проходит ближе всех других к ядру и градиент потенциальной энергии и сила здесь наибольшие.
21
. |
11 |
|
|
4 10 |
|
|
|
0 |
|
|
|
0 |
11 |
|
|
. |
|
|
|
2 10 |
|
|
|
Yp(z) |
|
|
|
Y |
|
|
|
|
0 |
|
|
|
5 .10 11 |
0 |
5 .10 11 |
|
|
0,0,z,Z |
|
Рис. 1. Траектории альфа-частицы с энергией 5 MeV |
|||
|
при рассеянии на ядре золота |
||
Извлечем компоненты скорости для k – ой траектории и определим кинетическую и потенциальную энергии частицы вдоль траектории. Построим графики кинетической, потенциальной и полной энергий в зависимости от времени. Здесь же с помощью маркера пометим начальную кинетическую энергию частицы Tα .
|
|
|
|
|
|
2 |
2 |
||
k := 0 |
vz := (Xk)2 |
vy := (Xk) |
4 |
r := |
(Xk)1 |
|
+ (Xk)3 |
||
|
|
|
(vz2 + vy2) |
|
|
|
|
|
|
T := (Xk)0 Ek := |
mα |
|
Ep := |
q1 q2 |
|
E := Ek + Ep |
|||
|
|
2 |
|
|
|
r |
|
|
|
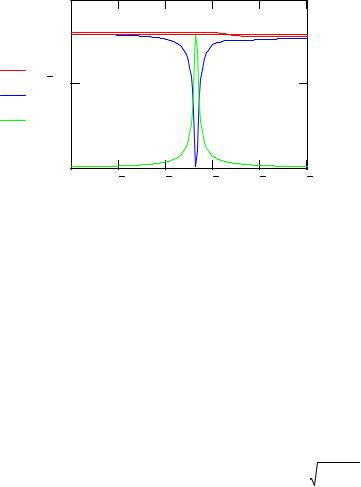
Изменяя k – номер траектории, можно увидеть, насколько хорошо сохраняется полная энергия вдоль каждой траектории. Апостериорные оценки показывают, что в результате накопления ошибок округления полная энергия сохраняется только с точностью порядка 2%. Причем наибольшее изменение происходит в окрестности точки разворота частицы. Кроме того, следует отметить, что полная энергия несколько выше начальной кинетической энергии частицы на входе в область взаимодействия. Это связано с тем, что начальные значения координат выбраны недостаточно далеко от рассеивающего центра и там полная энергия еще не определяется полностью кинетической. При сопоставлении траекторий с огибающей эти огрехи расчета еще не проявляются.
22
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tα |
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ek |
. |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ep |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
. |
19 |
2 |
. |
10 |
19 |
. |
19 |
4 |
. |
10 |
19 |
. |
19 |
|
|
|
|||||||||||||||
|
|
|
1 10 |
|
|
|
3 10 |
|
|
|
5 10 |
|
|||||
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
Рис. 2. |
К проверке сохранения энергии вдоль траектории |
|||||||||||||||
Потенциал Ленарда-Джонса
Рассмотрим рассеяние частицы с приведенной массой m = 20 a.u. в потенциале Ленарда - Джонса с параметрами, отвечающими взаимодействию двух атомов неона. В главе 2 такая задача уже рассматривалась в связи с процедурой расчета сечений рассеяния. Это позволяет сопоставить некоторые характеристики рассеивающейся частицы.
|
|
|
|
a |
12 |
a |
6 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
a := 2.74 A |
Vo := 0.0031 eV |
U(r) := 4 Vo |
|
|
|
|
− r |
||||
r |
|
|
|||||||||
Переопределим потенциал как функцию двух переменных на плоскости (z,y), выделяя область сильной отталкивательной сердцевины для того, чтобы обойти неприятности из-за сингулярности при построе-
нии графиков. ( ( ))
ε := 2.7 A Φ(z,y) := if z2 + y2 < ε2,U(ε),U z2 + y2
Определим проекции силы Fz и Fy как функцию переменных z и y
и используем уравнения движения в форме Ньютона. |
|
||||||
d |
|
d |
|
||||
Fz(z,y) := − |
|
|
Φ(z,y) |
Fy(z,y) := − |
|
|
Φ(z,y) |
|
|
||||||
dz |
|
dy |
|
||||
Пусть энергия частицы и ее масса, как и в гл. 2, составляют величины
23
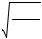
Eo := 0.8 Vo |
|
|
Eo = 2.48 × 10− 3 |
eV |
|||
mc2 := 20 931.5 106 |
|
mc2 = 1.863 × 1010 |
eV . |
||||
Начальная скорость частицы в единицах скорости света равна |
|||||||
c := 2.99793 10 |
10 |
cm |
V0 := |
2 Eo |
V0 = 5.16 × |
10 |
− 7 . |
|
s |
mc2 |
|
||||
Для сравнения с результатами гл. 2. при данной энергии интересно выбрать прицельный параметр около b = 4.8А, при котором наблюдалось рассеяние по спирали. Тогда оценка времени моделирования траекторий движения и начальные значения координат и скоростей для пяти траекторий с близкими прицельными параметрами равны
time := 20 |
a |
|
|
time = 1.062 × 108 |
a 1.7515 = 4.799 |
A |
||||||
V0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
K := 5 |
|
|
k := 0 .. K − 1 |
|
|
|
|
f |
|
|||
|
|
|
|
−3a |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
V0 |
|
|
|
|
|
|
Fz(f0,f2) |
|
|
|
|
|
|
|
|
||||||
f |
:= |
|
|
|
|
D(t,f) := mc2 |
|
|
||||
k |
|
|
|
+ 0.00045 k) |
|
|
|
|
|
f3 |
|
|
|
a (1.7515 |
|
|
|
|
|||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
Fy(f0,f2) |
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
mc2 |
|
|
||
Для решения системы уравнений движения воспользуемся встроенной функцией Bulstoer(.) или Radau(.).
Xk := Bulstoer(fk,0 ,time,200,D)
Для построения графика извлечем z и y – координаты всех траекторий и разместим их в едином массиве.
Z := augment (X0)1 ,(X1)1 ,(X2)1 ,(X3)1 ,(X4)1 Y := augment (X0)3 ,(X1)3 ,(X2)3 ,(X3)3 ,(X4)3
Как видно из рис. 3, все траектории начинаются в точке около z = 8 A и y = b = 4.8 A. Однако дальнейшее поведение траекторий очень разное. Незначительное изменение прицельного параметра приводит в дальнейшем к совершенно разным траекториям. Частица совершает разное число оборотов перед тем, как уйти от рассеивающего центра.
24
|
10 |
|
|
|
|
|
0 |
|
|
|
|
|
|
Y 0 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
Y 1 |
|
|
|
|
|
|
Y 2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Y 3 |
|
|
|
|
|
|
Y 4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 10 |
5 |
0 |
5 |
10 |
|
|
|
|
0,Z 0 ,Z 1 ,Z 2 ,Z 3 ,Z 4 |
|
||
Рис. 3. |
Рассеяние по спирали в потенциале Ленарда-Джонса |
|||||
Проанализируем изменение энергии вдоль траектории. Для этого извлечем компоненты скорости для k –ой траектории и определим кинетическую и потенциальную энергии частицы вдоль траектории. Построим графики кинетической, потенциальной и полной энергий в зависимости от времени. Здесь же с помощью маркера пометим начальную кинетическую энергию частицы Eo.
|
|
|
|
|
|
|
|
2 |
2 |
|||
k := 3 |
vz := (Xk)2 |
|
vy := |
(Xk) |
4 |
r := |
(Xk)1 |
|
+ (Xk)3 |
|
||
|
|
|
|
|
(vz2 |
+ vy2) |
|
|
|
|
|
|
T := (Xk)0 |
Ek := |
mc2 |
Ep := U(r) |
|
E := Ek + Ep |
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
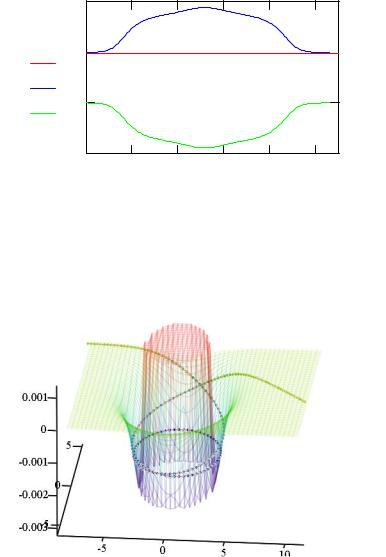
В отличие от случая кулоновского потенциала здесь вдоль траектории нет столь сильного градиента потенциала, сила, действующая на частицу, при почти круговом движении меняется слабо и потому заметного накопления ошибок округления не происходит. Плавное изменение потенциальной энергии компенсируется изменением скорости и кинетической энергии, а полная энергия остается постоянной и примерно равной начальной кинетической энергии.
25
E |
|
|
|
|
|
|
Eo |
|
|
|
|
|
|
|
|
Ek |
|
|
|
|
|
|
|
Ep |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 .107 |
4 .107 |
6 .107 |
8 .107 |
1 .108 |
|
|
|
|
|
T |
|
|
|
Рис. 4. |
К проверке сохранения энергии вдоль траектории |
|||||
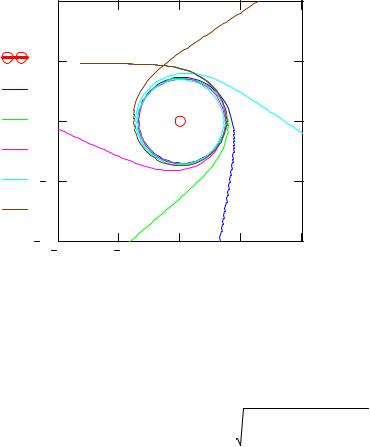
Визуально картина рассеяния по спирали очень наглядно представляется при анализе траектории на поверхности потенциальной энергии. Здесь отчетливо видно, что потенциальная энергия вдоль траектории меняется сравнительно медленно.
Φ,(Z k ,Y k ,Ep)
Рис. 5. Траектория на поверхности потенциальной энергии
26
Рассеяние в лабораторной системе координат
Выполним расчет траекторий двух взаимодействующих частиц в лабораторной системе координат. Пусть, например, атом Cu с энергией порядка E0 = 2 keV рассеивается на таком же покоящемся атоме. В качестве потенциала взаимодействия выберем потенциал Борна-Майера с параметрами (Гибсон-2) (см. [11])
Eo := 2 103 eV m1 := 29 931.5 106 eV ρ := 0.219 A
A := 2.2563 10 |
3 |
eV |
U(r) := A exp |
−r |
m2 |
:= m1 |
|
ρ |
|||||
|
|
|
|
|
|
Переопределим потенциал как функцию координат обеих частиц и проекции силы F12 , действующей на одну из частиц. По третьему закону Ньютона, сила, действующая на другую частицу, будет равна по модулю и противоположна по направлению.
|
−1 |
|
(z1 − z2) |
2 |
+ (y1 |
− y2) |
2 |
|||
Φ(z1,y1,z2,y2) := A exp |
|
|
|
|
|
|||||
|
ρ |
|
|
|
|
|
|
|
||
|
d |
|
|
|
|
|
|
|||
F12z(z1,y1,z2,y2) := |
− |
|
|
|
Φ(z1,y1 |
,z2,y2) |
|
|
||
|
|
|
|
|||||||
|
dz1 |
|
|
|
|
|||||
|
d |
|
|
|
|
|
|
|||
F12y(z1,y1,z2,y2) := |
− |
|
|
|
Φ(z1,y1,z2,y2) |
|
||||
|
|
|
|
|||||||
|
dy1 |
|
|
|
|
|||||
Поскольку характерное расстояние, на котором заметно изменяется потенциал Борна-Майера, равен параметру ρ , выберем начальные координаты (А) и проекции скоростей частиц (в единицах с) равными
zo1 := −1.0 |
yo1 := 0.035 |
zo2 := 0 |
yo2 := 0 |
|
Vzo1 := |
2 Eo |
Vyo1 := 0 |
Vzo2 := 0 |
Vyo2 := 0 . |
|
m1 |
|
|
|
Структуру вектора неизвестных и их начальные значения, а также структуру системы уравнений зафиксируем в векторах f и D(t,f). Время расчета оценим по порядку величины как начальное удаление частиц, деленное на начальную скорость. Траектории рассчитаем, используя встроенную функцию Rkadapt(.) или Radau(.).
time := |
2.5 |
|
zo1 |
|
|
time = 6.497 × 103 |
|
|
|||||
Vzo1 |
|
|
||||
|
|
|
|
|||
27

zo1Vzo1
yo1Vyo1 f := zo2Vzo2
yo2
Vyo2
|
|
|
|
f |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
F12z(f0 |
,f2 |
,f4 |
,f6) |
|
m1 |
||||||
|
|
|
|
f3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
F12y(f0 |
,f2 |
,f4 |
,f6) |
|
|
|
|
|||||
D(t,f) := |
m1 |
|
|
|
|
||
|
|
|
f5 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
||
|
|
|
|
F12z(f0,f2,f4,f6) |
|||
|
m2 |
||||||
|
|
|
|
f7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
F12y(f0 |
,f2 |
,f4 |
,f6) |
||
|
|
|
|||||
|
m2 |
|
|
|
|
||
X := Rkadapt(f,0 ,time,200,D)
Сгруппируем координаты и по наклону вектора скорости в последних точках оценим углы рассеяния θ1 и θ2 и параметры уравнений асимп-
тот к траекториям, а также расстояния |
0 и 1 от начала координат до |
||
точек пересечения асимптот. |
|
|
|
Z1 := X 1 |
Y1 := X 3 |
vz1 := X 2 |
vy1 := X 4 |
Z2 := X 5
N := rows(X) − 1
tgθ1 := vy1N vz1N
θ1 := atan(tgθ1)
n := 0 .. 1
Y2 := X 7 |
vz2 := X 6 |
vy2 := X 8 |
N = 200 |
|
|
tgθ2 := vy2N vz2N
θ1 = 1.201
zN := Z1N
Z2N
θ2 := atan(tgθ2)
yN := Y1N
Y2N
θ2 = −0.383
|
|
|
|
− tgθn+1 zN |
−0.234 |
|
|
d |
n |
:= yN |
n |
d = |
0.077 |
|
|
|
|
n |
|
|
|||
yo1 |
|
|
Yon − dn |
|
0.104 |
|
|
Yo := |
|
n := |
|
= |
0.191 |
|
|
tgθn+1 |
|||||||
yo2 |
|
|
|
28
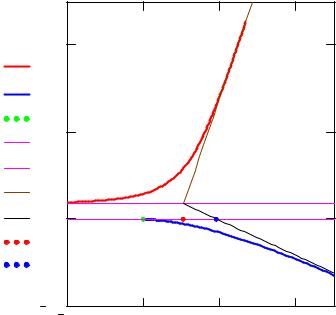
Определим уравнения асимптот и построим траектории, их асимптоты и |
||||||||
отметим координаты точек их пересечения на оси системы. |
|
|||||||
y1(z) := tgθ1 z + d |
0 |
y2(z) := tgθ2 z + d |
1 |
z2 := |
0, |
0 + 0.01 .. zN |
||
|
|
|
|
|
|
1 |
||
Y1 |
0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y2 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
yo1 |
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
y1(z2) |
|
|
|
|
|
|
|
|
y2(z2) |
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0.2 0.2 |
|
0 |
0.2 |
|
0.4 |
|
|
|
|
|
Z1,Z2,0,z,z,z2,z2, 0, 1 |
|
|
|||
Рис. 6. Траектории рассеяния двух атомов меди в |
лабораторной |
|||||||
|
системе координат в потенциале Борна-Майера |
|
||||||
Следуя методике, изложенной в главе 2, оценим угол рассеяния χcm в системе центра масс и углы рассеяния в лабораторной системе. Прицельный параметр и энергия относительного движения в системе центра масс равна (см. [10–12])
|
|
|
|
|
|
|
m1 m2 |
2 |
|
3 |
|
|
b := yo1 |
|
|
|
Ecm := |
|
Vzo1 |
Ecm = 1 × 10 |
|
eV |
|||
|
|
|
2 (m1 + m2) |
|
||||||||
|
b |
2 |
U(x) |
|
|
|
|
|
||||
f(x ,b) := 1 − |
|
|
|
− |
|
|
rn := root(f(x ,b) |
,x ,b ,1) rn = 0.186 |
A |
|||
x |
Ecm |
|||||||||||
|
|
|
|
|
|
|
||||||
29
|
|
|
⌠ |
∞ |
|
||
χcm := π − 2 b |
|
1 |
|
dx |
|||
|
|
x2 f(x ,b) |
|||||
|
|
|
|
|
|
||
|
|
|
⌡rn |
|
|||
|
|
|
sin(χcm) |
|
|||
θth1 |
:= atan |
|
|
|
|
|
|
m1 |
|
|
|
||||
|
|
+ cos(χcm) |
|
||||
|
m2 |
|
|
|
|
||
χcm = 2.398
θth2 := |
π − χcm |
|
2 |
Сопоставляя результаты, обнаруживаем заметную (порядка 3%) ошибку в расчете угла отклонения первоначально покоившейся частицы.
θth1 = 1.199 |
θ1 = 1.201 |
θth2 = 0.372 |
θ2 |
= 0.383 |
Проанализируем изменение кинетической и потенциальной энергии для каждой частицы вдоль траектории и оценим значения теряемой и передаваемой энергии частицами в процессе столкновения.
T := X 0 |
r := (Z1 − Z2)2 + (Y1 − Y2)2 |
Ep := U(r) |
|||
Ek1 := |
m1 |
(vz12 + vy12) |
Ek2 := |
m2 |
(vz22 + vy22) |
|
2 |
|
|
2 |
|
Энергии частиц в конце упругого столкновения определяются законами сохранения энергии и импульса и задаются соотношениями [10-12].
|
m1 |
|
2 |
|
|
m2 |
2 |
2 |
|||
|
|
cos(θth1) + |
|
− sin(θth1) |
2 |
||||||
E1 := Eo |
|
|
|
|
|
|
|
|
|||
m1 + m2 |
|
|
|
m1 |
|||||||
|
|
E2 := Eo |
4 m1 m2 |
|
cos(θth2)2 |
|
|||||
|
(m1 + m2) |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Сопоставляя энергии, обнаруживаем заметное (порядка 7%) отличие в энергии налетающей частицы после рассеяния.
E1 |
= 264.144 |
eV |
E2 = 1.736 × 103 |
eV |
Ek1N = 278.856 |
eV |
Ek2N = 1.739 × 103 |
eV |
|
E1 |
+ E2 = 2 × 103 |
|
Ek1N + Ek2N = 2.017 × 103 |
|
Etot := Ek1 + Ek2 + Ep |
EpN = 5.894 eV |
|
||
30
