SimulationPhysProc_1_81

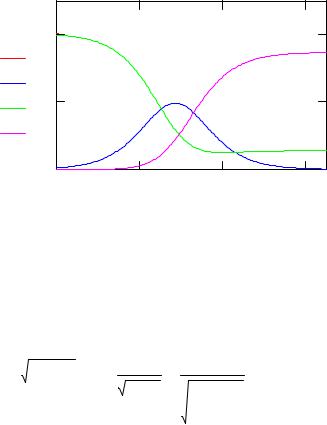
Общая динамика изменения энергии в процессе рассеяния представлена на рис. 7. Поскольку потенциальная энергия к моменту окончания расчета еще не равна нулю, то частицы еще не вышли на точную асимптотику. Это может частично, наряду с накоплением ошибок в процессе моделирования, объяснять отличие в значениях кинетической энергии. Полная энергия с очень хорошей точностью сохраняется.

При анализе траектории в случае коррелированных столкновений, например, в твердых телах, когда налетающая частица испытывает последовательные рассеяния на нескольких атомах решетки, знание асимптот предыдущего столкновения позволяет оценить прицельный параметр для следующего столкновения [11]. Для такой оценки важную роль играет интеграл времени столкновений (имеющий размерность длины). Оценим его в условиях данной задачи.

Зная интеграл времени, можно оценить координаты точек пересечения асимптот к траекториям с помощью соотношений (см. [11-12])

31

Сопоставляя эти значения с рассчитанными выше по наклону траекторий, отмечаем, что погрешность составляет порядка 6%. Ясно, что эти характеристики траекторий являются наиболее чувствительными к ошибкам, вносимым численным методом, поскольку небольшое изменение углов наклона асимптот может вызывать заметные погрешности в координатах точек их пересечения.

Точностью решения уравнений с помощью встроенных функций MathCAD можно управлять, изменяя параметр TOL, т.к. с его помощью контролируется точность вычисления интегралов или интегральных сумм. Однако точность расчета характеристик траекторий следует анализировать в каждом конкретном случае.

Упражнения

1.Исходя из законов сохранения энергии и момента импульса альфачастицы при рассеянии на кулоновском силовом центре, получите приведенные выше уравнения траектории (cм. [8]). Сравните рассчитанные траектории при выбранных параметрах с аналитическим решением.

2.При рассеянии в кулоновском поле можно считать r(b) и θ(b) функциями параметра b и представить уравнение траектории в виде

Если семейство кривых допускает огибающую (и нет особых точек), то приведенное выше уравнение огибающей получается из системы

db

3.Используя решение задачи о расчете траекторий альфа-частицы в поле ядра, построить зависимости координат и скоростей от времени, а также фазовые диаграммы (z,Vz) и (y,Vy). По поведению зависимости от координаты z отношения Vy/Vz оценить асимптотическое значение угла рассеяния и сравнить с результатами, получаемыми с помощью формулы Резерфорда.

4.Для притягивающего кулоновского взаимодействия с параметрами, аналогичными описанным выше, построить семейство траекторий и сравнить их с аналитическим решением. Рассчитать связь прицельных

32

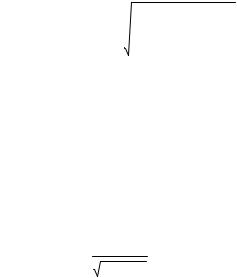
параметров и углов рассеяния. По поведению в зависимости от координаты z отношения Vy/Vz оценить асимптотическое значение угла рассеяния и сравнить с результатами, получаемыми с помощью формулы Резерфорда.

5.Предложить процедуру расчета траекторий в кулоновском потенциале для задачи рассеяния альфа-частиц, основанную на использовании встроенных функций MathCAD и обеспечивающую точность выполнения закона сохранения энергии выше, чем это было получено в тексте.

6.Зафиксировав входные данные в задаче о рассеянии частицы на потенциале Ленарда-Джонса, рассчитать несколько траекторий, используя разные встроенные функции MathCAD для решения задачи Коши для систем обыкновенных дифференциальных уравнений. Сравнить найденный по траектории угол отклонения частицы с результатом расчета

вглаве 2. Какой встроенной функции Вы отдали бы предпочтение?

7.Построить семейство траекторий с разными прицельными параметрами и их огибающих при рассеянии двух атомов меди в лабораторной системе в потенциале: а) Гибсон-2, б) Морса с параметрами из [11].

8.Используя законы сохранения энергии и импульса, получить соотношения, связывающие значения энергий частиц после упругого столкновения с энергией налетающей частицы. Перед радикалом следует выби-

рать знак минус в случае, если m1 > m2 .

9.Для нескольких значений энергии налетающей частицы рассчитать

впотенциале Циглера - Бирзака -Литтмарка ([11,12]): а) связь прицельных параметров и углов рассеяния в системе центра масс; б) интеграл времени, вычисляя интегралы методом Гаусса-Лежандра.

10.При нескольких значениях энергии рассчитать интеграл времени для потенциалов: a) Морса, б) Ленарда-Джонса, считая, что при притягивающем потенциале (b > rmin) интеграл времени определяется как (см.[11])

33

Глава 4. Динамические траектории химических реакций

Для химической реакции обмена между атомом А и молекулой ВС А + ВС –> АВ + С построим поверхность потенциальной энергии и методом классических траекторий в коллинеарном приближении рассчитаем динамические траектории на поверхности потенциальной энергии для реакции Н + Н2 –> Н2 + Н .

Метод классических траекторий

Классические траектории для атомов при описании химических реакций можно рассматривать лишь при условии, что дебройлевские длины волн участвующих в реакции атомов значительно меньше расстояний между ними. Это требование ограничивает снизу диапазон допустимых энергий налетающей частицы. Метод классических траекторий для трехчастичной системы состоит в решении классических уравнений движения для каждого атома при различных начальных конфигурациях. Последующее усреднение позволяет находить сечения и константы скорости некоторых атомных процессов и химических реакций [13–14 ].

Поскольку кинетическая энергия системы как целого не влияет на относительное движение частиц, положим суммарный импульс систе-

мы равным нулю, а начало координат выберем в центре масс системы.

→ → →

p1 + p2 + p3 = 0

m1 r1 + m2 r2 + m3 r3 = 0

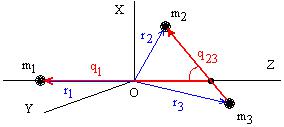
Вместо обычных координат введем в рассмотрение координаты Якоби, характеризующие относительное положение частиц в паре, например, (2,3), и положение частицы 1 относительно центра масс пары (2,3). При этом число независимых внутренних геометрических параметров уменьшается до 3N– 6 = 3. Пусть частицы расположены в плоскости XZ и ось Z направлена вдоль вектора относительной скорости V 1,23 на большом удалении(см. рис.1).

34

где μ23 и μ1– приведенные массы пары (2,3) и частицы 1 и пары (2,3). Обратный переход к координатам r1,r2 и r3 производится по формулам:

отсюда относительные координаты в двух других парах частиц равны:

а относительные импульсы определяются по формулам:

Рис. 1. Координаты Якоби в трехчастичной системе В рамках полуклассического приближения предполагается, что ядра

следуют вдоль классических траекторий, определяемых заданной поверхностью потенциальной энергии всей системы, а гамильтониан трехчастичной системы может быть представлен в виде [13–14 ]:

35

начальных условий эти уравнения движения могут быть решены какимлибо численным методом.

Выбор потенциальной энергии взаимодействия в системе

Построение поверхности потенциальной энергии представляет собой сложную задачу, требующую квантово-механических расчетов для рассматриваемой модели –системы ядер и электронов. Решить такую задачу исходя из первых принципов (ab initio) не всегда можно. Поэтому разумной альтернативой является использование согласованных с экспериментом полуэмпирических аппроксимаций.

Одним из наиболее часто используемых приближений для описания поверхности потенциальной энергии для реакции А + ВС–> АВ + С яв-

ляется функция типа London–Eyring–Polanyi–Sato (LEPS) (см.[14]). Она основана на использовании функции Морса и задается следующим образом. Пусть Qab, Jab, Sab и т.д. – кулоновские, обменные интегралы и интегралы перекрывания для соответствующих пар атомов. Если D, β и r0 – параметры парной потенциальной функции Морса (см. [13])

V(r) = D exp −2 β (r − r0) − 2 exp −β (r − r0) ,

то кулоновские и обменные интегралы представляются формулами, например, в паре AB

Интегралы перекрывания S играют роль подгоночных параметров в потенциальной энергии системы U(rab,rbc,rac) вида:

36

Uj(rab,rbc,rac) = J1(rab,rbc) + J2(rbc,rac) + J3(rac,rab)

U(rab,rbc,rac) = Uq(rab,rbc,rac) − Uj(rab,rbc,rac)

Реакция обмена H + H2 –> H2 + H

Рассмотрим реакцию обмена между молекулой и атомом водорода в коллинеарном приближении, т.е. предполагаем, что все три атома водорода в процессе реакции двигаются только вдоль оси молекулы. Тогда массы всех трех частиц, энергии диссоциации D, равновесные расстояния в молекуле q0, параметры β и интегралы для всех пар одинаковы. Выберем следующие значения (см. [13,14]) и построим функцию U.

37

Uj(q12 ,q23 ,q13) := J1(q12 ,q23) + J2(q23 ,q13) + J3(q12 ,q13) U(q12 ,q23 ,q13) := Uq(q12 ,q23 ,q13) − Uj(q12 ,q23 ,q13)

Поскольку в линейной геометрии (см. рис. 1) угол между векторами q1 и q23 равен нулю, то

и поверхность потенциальной энергии U(q12 ,q23 ,q13) удобно рас-

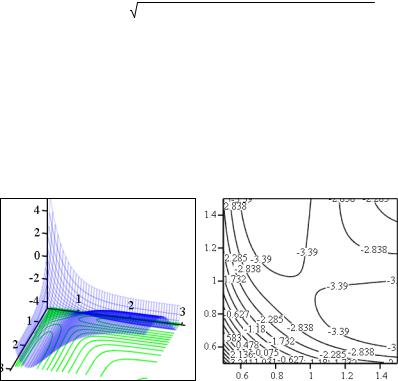
сматривать как функцию переменных q12 и q23. Построим ее поверхностный и контурный графики (см. рис. 2).

Φ(q12 ,q23) := U(q12 ,q23 ,q12 + q23)

Рис. 2. Потенциальная энергия для линейной реакции Н + Н2 –> Н2 + Н

Как видно из рис. 2, асимптотически при больших расстояниях в парах частиц сечение поверхности плоскостью, перпендикулярной оси, напоминает график функции Морса, минимумы которой дают начало двум долинам, которые соединяются в седловой точке около (q12 = 1, q23 = 1).

Принимая во внимание симметричность поверхности, оценим изменение энергии при переходе из одной долины в другую – высоту классического барьера (при q12 , q23 >> q0) и сравним с ab initio-расчетом.

Следовательно, полуэмпирические аппроксимации типа LEPS могут лишь качественно передавать структуру поверхности потенциальной энергии для реакции Н + Н2 –> Н2 + Н.

38

Уравнения движения

Для записи уравнений движения учтем равенство масс частиц и представим потенциальную энергию в переменных Якоби посредством соотношения

UJ(q1,q23) := U(q1 − 0.5 q23 ,q23 ,q1 + 0.5 q23).

Тогда уравнения движения в переменных Якоби принимают вид:

Начальное состояние атома и молекулы

Будем считать, что начальное состояние атомов в молекуле H2 (паре23) можно описывать потенциалом Морса с выбранными выше параметрами. Если задана энергия атомов в молекуле Е23 и скорость относительного движения атомов молекулы v23 , то можно оценить начальное зна-

чение координаты q023 с помощью соотношений

V(r) := D exp −2 β (r − q0) − 2 exp −β (r − q0)

сти света. Типичные значения энергии и скорости атомов в молекуле равны (см. [13])

39

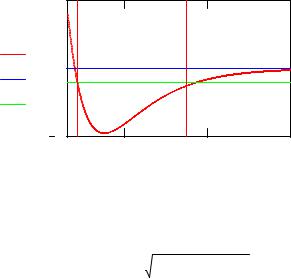
Рис. 3. К выбору начальных координат атомов. Если положить импульс р23 равным нулю, то х1 и х2 будут классическими точками поворота

v230max := 2 mc2− 1 (e23 + D)

скорость может принимать значения в интервале (в единицах с) [ 0, v230max= 1.265× 10− 4 ] ,

принимают значения в интервале [ X1 = 0.414 , X0 = 1.872 ] А.

В системе центра масс атом и молекула сближаются с одинаковыми импульсами. Типичное значение скорости относительного движения атома и молекулы для этой реакции тоже составляет величину порядка V = 106 см/s . Пусть начальные относительные координата и скорость атома и молекулы имеют значения

Решение уравнений движения

Если расстояния измеряются в ангстремах (А), скорости – в единицах скорости света (с), энергии – в электрон-вольтах (eV), то время должно измеряться в единицах А/c для того, чтобы форма уравнений движения не изменилась. Тогда предполагаемое время расчета в этих единицах равно

40