SimulationPhysProc_1_81

Упражнения

1.Используя символьный процессор MathCAD, получить обсуждавшееся выше стационарное решение для концентраций вакансий и межузельных атомов. Найти предельные выражения для случая: а) преимущественной взаимной рекомбинации; б) преимущественного ухода дефектов на стоки.

2.Показать, что критерием в двух предельных случаях, соответствующих: а) преимущественной взаимной рекомбинации (φ >>1); б) ухода дефектов на стоки (φ <<1) может служить параметр φ, равный (см.[15])

где исходная плотность дислокаций и интенсивность нейтральных стоков в данном случае приняты равными 108 cm-2. Рассчитать зависимости концентраций дефектов от времени в этих предельных случаях.

3. В условиях данной задачи рассчитать зависимость от времени диф-

фузионных потенциалов Fi = Zi Di Ci и Fv = Zv Dv Cv . Проанализировать их роль в установлении стационарных концентраций и оценить

время выхода на стационарный уровень.

4. Выполнить расчет зависимости концентраций дефектов от времени для кристалла никеля: а) в условиях активной зоны быстрого реактора, Gi = Gv = 10-6 dpa/s и Temp = 625 ÷ 925K; б) внутренней стенки корпуса

теплового реактора, Gi = Gv = 10-9 dpa/s и Temp = 565K. Как зависит индекс жесткости системы уравнений от температуры никеля?

5. Построить неявную разностную схему на основе метода Эйлера для решения жесткой системы уравнений, обсуждаемой в данной главе. Разработать алгоритм численного решения получающейся системы нелинейных уравнений итерационным методом Ньютона. Проанализировать условия сходимости и оценить скорость метода в данной задаче. На основе разработанного алгоритма написать программу и проверить

ееэффективность для данной задачи.

6.Предложить неявную разностную схему для решения данной задачи методом Рунге-Кутты, обладающую свойством A(α) – устойчивости.

7.Определить особые точки данной системы дифференциальных урав-

нений и построить фазовые портреты в окрестности этих точек.

8. Используя разные встроенные функции MathCAD для решения систем обыкновенных дифференциальных уравнений, получить решение данной задачи для концентраций точечных дефектов. Проанализировать точность и скорость сходимости результатов. Какой встроенной функции Вы бы отдали предпочтение?

51

Глава 6. Динамика излучения лазера

Необходимым условием для работы лазера является создание инверсии населённостей активных атомов такого состояния среды, когда населённость уровней с большей энергией превышает населённость уровней с меньшей энергией. Создание и поддержание инверсной заселённости атомов лазерной среды возможно только при вложении в среду энергии от внешнего источника (накачка лазера), которое в зависимости от конкретных условий может быть реализовано различными способами.

В настоящее время широкое распространение получили следующие способы накачки лазеров: электрический разряд; накачка пучком быстрых частиц (электронов, протонов, ионов); оптическая накачка; накачка энергией химических реакций; накачка продуктами ядерных реакций (осколки деления урана, протоны, α-частицы).

В процессе генерации лазерного излучения происходит резонансное взаимодействие интенсивной электромагнитной волны с активными атомами лазерной среды. Динамика развития, установления и поддержания лазерной генерации существенно зависит от соотношения скоростей релаксации интенсивности излучения и характеристик резонансных атомов: поляризации и населённостей рабочих уровней. Основной задачей данной главы будет расчет зависимости от времени заселенностей уровней энергии атомов рабочей среды, анализ смены режимов генерации лазера в рамках простейшей модели (имеющей, тем не менее, большое практическое применение). При изменении соотношений между скоростями релаксации можно проследить переход от стабильной генерации с различными законами установления к бистабильности и генерации периодической последовательноcти импульсов – пичковой и хаотической генерации.

Модель газового лазера

Рассмотрим простейшую модель четырехуровневого лазера. Важными примерами подобных систем могут быть лазеры на неодимовом стекле Nd+3 и CO2 -лазеры. Следуя [17-18], примем следующую схему создания и снятия возбуждения (релаксации) для четырех–уровневого лазера. Атомы рабочей среды в результате накачки переходят из основного состояния 0 в возбужденное 3. Из этого состояния 3 атомы очень быстро и без излучения переходят на метастабильный уровень 2, на котором они могут находиться сравнительно долго. Таким образом создается инверсная заселенность уровней 1 и 2. В процессе спонтанных переходов атомов с уровня 2 на уровень 1 в резонаторе возникают фотоны, которые путем стимулирующего воздействия на атомы среды, находящиеся на уровне 2, вызывают лавину когерентного излучения.

52

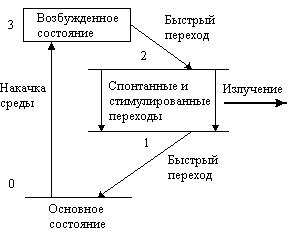
Рис. 1. Схема создания и снятия возбуждения атомов рабочей среды

Этой модели соответствует следующая система уравнений, описывающая изменение во времени средних населенностей атомов на уровнях N1 и N2 и спектральной плотности энергии в резонаторе W.

Здесь A21 и B21 – коэффициенты Эйнштейна спонтанного и вынужденного излучения для перехода 2 –> 1 соответственно. Скорость накачки атомов на уровень 2 характеризуется параметром R, а параметры Т0, Т1 и Т2 задают время жизни фотонов в резонаторе и постоянные времени уровней 1 и 2. В данной модели предполагается, что лазер работает в одномодовом режиме, соответствующем центру лоренцовской спектральной линии. Излучаемые фотоны имеют энергию hν , а амплитуда лоренцовской линии определяется соотношением g(ν) = 4/(A21 + 1/T1).

При этом скорость спонтанного перехода 2 –> 1 в центральной моде характеризуется коэффициентом Эйнштейна a21, который обычно много меньше суммарного A21.

53

Стационарный режим работы лазера

Полагая производные по времени равными нулю и пренебрегая коэффициентом а21, найдем стационарные решения данной системы уравнений. Воспользовавшись символьным процессором MathCAD, получаем два решения, одно из которых соответствует безизлучательному режиму работы лазера

а второе стационарное решение c W > 0 и постоянной разностью населенностей имеет вид

Для того, чтобы избежать больших порядков значений рассчитываемых величин выберем в качестве размерных масштабов времени Т2 и А21, накачки Rc, населенности Nc = Rc/A21 как на пороге генерации и отношение коэффициентов Эйнштейна B21/A21 для спектральной плотности энергии.

Тогда система уравнений для безразмерных населенностей на уровнях n1 и n2 и энергии w и их начальные значения принимают вид:

54

t

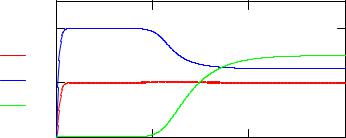
Рис. 2. Временная динамика населенностей и плотности энергии лазера

55

Как видно из рис. 2, населенности атомов в течение времени порядка Т0 резко нарастают, в то время как плотность энергии излучения практически равна нулю. Система переходит в неустойчивый режим с инверсной заселенностью и через время порядка (5-10)Т2 начинается генерация излучения. В течение этого времени населенность на уровне 1 остается практически постоянной, а на уровне 2 – быстро падает и это сопровождается резким нарастанием энергии излучения. Наличие двух существенно различных масштабов времени объясняется малостью отношения скоростей распада основной моды и всего спектра а21/A21.

Стабильная генерация

Исследуем характерные особенности решений балансных уравнений лазера. Эти уравнения в силу своей простоты и наглядности играют в динамической теории лазеров особую роль, поскольку в них учитываются только самые фундаментальные процессы взаимодействия поля излучения с атомами и пренебрегается всеми сопутствующими, усложняющими теоретический анализ процессами. Система балансных уравнений лазера, включающая в себя уравнения для изменения интенсивности излучения I и коэффициента усиления лазерной среды αус, может быть записана в следующем виде:

ddtI = c (αус − αосл)I

где c – скорость света; γ || – скорость релаксации разности населённо- стей (скорость продольной релаксации); Iнас – интенсивность насыще-

ния (характерная интенсивность, при превышении которой становятся существенными процессы вынужденного испускания излучения); αосл = ln(1/R1R2) / 2L – коэффициент ослабления, обусловленного выходом излучения из лазера через зеркала резонатора с коэффициентами отражения R1 и R2; L – длина активной среды лазера; α0 – ненасыщенный коэффициент усиления (коэффициент усиления без учёта процессов вынужденного испускания и поглощения излучения – линейный коэффициент усиления).

Перейдём в системе уравнений к безразмерным переменным:

56

Стационарные решения (особые точки системы уравнений) соответствуют следующим физическим ситуациям: отсутствие генерации лазера (решение с J =0) и её наличия. Реализация одного из стационарных решений зависит от того, какая при заданных условиях (величины параметров Q и k заданы) особая точка устойчива.

Для нахождения условий устойчивости стационарных решений следует линеаризовать систему в окрестности каждого из них по малым отклонениям

получить характеристическое уравнение и проанализировав его корни, определить тип особой точки. Указанная подстановка приводит к следующим характеристическим уравнениям для первого и второго решения, соответственно.

Условием устойчивости стационарного решения системы нелинейных дифференциальных уравнений является отрицательность действительной части решения характеристического уравнения. Характеристическое уравнение для режима без генерации имеет следующие решения:

знак второго из которых зависит от величины параметра Q. Если Q < 1, то оба корня отрицательны и стационарное решение системы устойчиво (тип особой точки – устойчивый узел). Если же Q > 1, то второй корень положителен и решение становится неустойчивым (особая точка

– седло). Это неравенство выражает условие самовозбуждения лазера

Q = α0 > 1 .

αосл

57

Если Q < 1, т. е. линейное усиление излучения меньше потерь, то генерация лазерного излучения отсутствует – это состояние лазера описывается стационарным решением с J =0, которое в данном случае устойчиво. В случае же Q > 1, когда линейное усиление превышает потери, генерация излучения становится возможной и это решение перестаёт быть устойчивым.

Генерационное состояние лазера описывает решение с J = Q – 1. Соответствующее ему характеристическое уравнение имеет корни:

Из этого выражения прежде всего видно, что при Q < 1 один из корней характеристического уравнения положителен. Следовательно, в этом случае решение с J = Q – 1 неустойчиво (особая точка – седло).

Отрицательными же действительные части становятся при Q > 1, что говорит об устойчивости решения в этом случае.

Проведённый анализ показал, что любое возмущение электромагнитного поля в резонаторе лазера будет стремиться либо к стационарному решению с J = 0, когда условие самовозбуждения лазера не выполняется и генерация невозможна, либо при выполнении условия самовозбуждения к стационарному решению с J = Q – 1, описывающему генерационное состояние лазера. Если параметр Q в исходном уравнении является медленной функцией времени, то во втором случае после прекращения переходного процесса интенсивность лазерного излучения будет тоже функцией времени. В этом случае будет протекать, так называемая, квазистационарная генерация лазера.

Характер динамики установления стационарной (квазистационарной) генерации зависит от того, действительны или комплексно-сопряжены корни характеристического уравнения, что определяется знаком подкоренного выражения. Если Q2/4 > k (Q-1), то подкоренное выражение в положительно и оба корня – действительные числа. В этом случае особая точка – устойчивый узел, и будет протекать апериодический процесс установления генерации лазера. Если же выполняется обратное

неравенство Q2/4 < k (Q-1), то подкоренное выражение отрицательно и корни являются комплексно-сопряжёнными. Процесс установления стационарной генерации в этом случае будет иметь характер затухающих колебаний с периодом Т и декрементом затухания Г (см упр. 11). Стационарное решение в этом случае – устойчивый фокус. Реализация одного из сценариев установления стационарной генерации лазера зависит как от величины превышения порога генерации (значение параметра Q), так и от значения параметра k = cα осл/γ ||, который имеет

58

смысл отношения скорости затухания поля излучения в резонаторе к скорости релаксации разности населённостей активных атомов лазерной среды. Однако поскольку на пороге генерации в момент начала её развития Q ≈1 (незначительно превышает 1), то на практике определяю-

щим обычно является соотношение между cαосл и γ ||. Первый, апериодический режим установления генерации реализуется в газовых

лазерах, у которых cαосл << γ || ~ 108 – 109 c-1 (соответственно k << 1). У широко распространённых твердотельных лазеров (неодимовый, рубиновый) имеет место обратное неравенство cαосл >> γ || ~ 103 – 104 c-1 (соответственно k >> 1) и для них характерным является установление генерации посредством затухающих колебаний.

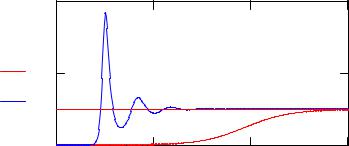
Выполним решение системы уравнений для интенсивности J и коэффициента усиления α. Выберем начальные условия, сформируем правую часть системы уравнений и построим графики изменения интенсивности при выходе на стационарный уровень в апериодическом режиме (k = 0.9) и режиме затухающих колебаний (k = 15). Маркером укажем положение стационарного решения J2.

59