
МОМ - частная методика
.pdf
Тест
Вычислить:
4
Г. ∫(dx)/x²
2 |
2) ¾; |
3) |
¼. |
1) -1/2; |
|||
1 |
3 |
|
|
|
|
|
|
Д. ∫(√x+√x)dx |
|
|
|
0 |
2) 1/6; |
3) |
17/12. |
1) 5; |
|||
Итог работы
Оцените себя: как вы работали на
уроке?
Что удалосьсделать легко? Почему?
В чём вы испытали трудность?
Почему?
Что могли сделать лучше?
Сегодня мы с вами ещё раз убедились в том, что наука покоится на великих истинах. Решая задачи, вы пользовались тем, что когда-то уже доказали люди. Какое же влияние оказали на вассегодняшние умственные
занятия?
Домашнее задание
Подготовить сообщение о
применении интеграла в практических задачах.
Составить задачи о применении
интеграла.
III.Внеаудиторное задание.
(1)Составьте и заполните технологическую карту урока по теме Свойства неопределённого интеграла.
(2)Проведите анализ одного из уроков по теме «Первообразная. Интеграл»
–http://festival.1september.ru/articles/102035/,
–http://festival.1september.ru/articles/565996/,
–http://festival.1september.ru/articles/212241/.
(3)Разработайте ЦОР по теме «История возникновения и развития математического анализа».
(4)Протестируйте программу VIP Test (http://festival.1september.ru/articles/585143/). Создайте базу вопросов по теме
«Первообразная и интеграл».
(5)Рассмотрите возможность изучения материала изложенного в книге В.В. Скворцова «Нескучные вычисления» на уроках математики в 11 классе (разработайте план-конспект урока).
51

Лабораторная работа «Изучение первообразной функции и интегралов: дифференциальные уравнения в ШКМ»
Задание 1. Изучите содержание лекции, разработанной учителем математики Т.А. Лукьяновой (http://festival.1september.ru/articles/534688), и
разработайте систему упражнений на усвоение лекционного материала.
|
|
Лекция для слушателей элективного курса по теме |
Упражнения на усвоение |
|||||
|
|
|
«Дифференциальные уравнения и их приложения |
|||||
|
|
|
изученного материала |
|||||
|
|
|
|
в естествознании» |
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
1. Дифференциальные уравнения |
|
|
|
В ходе решения задач естествознания часто возникают |
|
||||||
соотношения, связывающие производные некоторой функции |
|
|||||||
(первую, вторую и т. д.) саму эту функцию и независимую |
|
|||||||
переменную. |
|
|
||||||
|
Например, согласно второму закону Ньютона при движении |
|
||||||
по прямой материальной точки постоянной массы m |
|
|
||||||
справедлива формула F= ma, где F – сила, вызывающая |
|
|||||||
движение, a – ускорение точки. |
|
|
||||||
|
Пусть F зависит только от времени t, т.е. F= F(t) . |
|
|
|||||
Вспоминая, что ускорение есть вторая производная координаты |
|
|||||||
по времени a(t) = х (t), получаем дифференциальное |
|
|
||||||
уравнение относительно функции x(t): F(t) = mх (t), т.е. |
|
|||||||
|
|
|
F(t) |
|
|
|||
(t) |
|
|
, для решения которого сначала находим х |
(t) как |
|
|||
x |
|
|
|
|||||
|
|
|
m |
|
|
|||
первообразную функции |
F(t) |
, а затем и х (t) как |
|
|
||||
|
|
|
||||||
|
|
|
|
|
m |
|
|
|
первообразную функцию v(t) = х (t). |
|
|
||||||
|
Общее решение зависит от двух произвольных постоянных. |
|
||||||
Для того чтобы их найти, обычно задают координату и |
|
|
||||||
скорость в какой-то момент времени t. |
|
|
||||||
|
Определение. Уравнение вида F(х, у, у ,…,у(n)) =0, |
(1) |
|
|||||
где у = у(х) – искомая функция, называется дифференциальным |
|
|||||||
уравнением n-го порядка. |
|
|
||||||
|
Любая функция y = (х), обращающая уравнение (1) в |
|
||||||
тождество, называется решением этого уравнения. |
|
|
||||||
|
Если в обычных уравнениях, решаемых в школе, требуется |
|
||||||
найти численные значения некоторой переменной, то в |
|
|
||||||
дифференциальном уравнении искомой является функция, |
|
|||||||
причём в уравнение входит производная этой функции. |
|
|
||||||
Простейшими являются |
|
|
||||||
–уравнения показательного роста (или убывания) у =ky, (2)
где у = у(х) – неизвестная функция, k ≠ 0 – заданная постоянная,
–уравнение гармонических колебаний у = – 2y,
(3)где у – неизвестная функция, > 0 – постоянная.
В различных областях человеческой деятельности возникают задачи, сводящиеся к дифференциальным уравнениям. Характер этих задач и методику их решения можно описать примерно так. Изучается какой-нибудь процесс – физический, биологический и т. д. Нас интересует изменение во времени какой-то характеристики этого процесса, то есть некоторой величины ( температуры, давления, массы и т. п.). Если у нас имеется достаточно много сведений о течении этого процесса,
52

мы можем попытаться построить его математическую модель. Во многих случаях из экспериментальных данных или из физических и прочих законов удаётся получить информацию о скорости изменения величины у = у(t) в зависимости от времени t, то есть от производной у = у (t). Эта информация обычно может быть записана в виде дифференциального уравнения с неизвестной функцией у = у(t). Получающееся уравнение как раз и описывает наш процесс с точки зрения его характеристики у. Отыскав все решения дифференциального уравнения – само по себе это уже чисто математическая задача, мы находим все возможные варианты изменения величины у. Отметим, что при математическом описании всегда приходится делать некоторые упрощающие предположения, пренебрегать теми или иными побочными явлениями, принимать «идеальные условия» – одним словом, абстрагироваться от конкретных деталей. Это приводит к известным ограничениям в применимости построенной модели.
Опыт развития различных наук показывает, что многие далёкие друг от друга по содержанию задачи приводят к одинаковым или сходным дифференциальным уравнениям. Поэтому естественно разработать методы решения таких уравнений безотносительно к тем задачам, которые привели или могут привести к ним. Этим как раз и занимается математическая теория дифференциальных уравнений.
Если какая-нибудь задача сводится к дифференциальному уравнению, методы решения которого уже известны, то эту задачу можно считать решённой. В этом случае творческая часть решения заканчивается составлением дифференциального уравнения, второй же этап – отыскание решений уравнения – будет представлять собой хотя и важную, но чисто техническую задачу.
Начнём наше знакомство с самых простых дифференциальных уравнений – линейных.
2. Линейные дифференциальные уравнения
Уравнение у =ky называется линейным, поскольку неизвестная функция у и её производная у входят в него линейным образом. Известно, что любое решение этого уравнения записывается в виде у=Аеkх, (4) где А – произвольная постоянная.
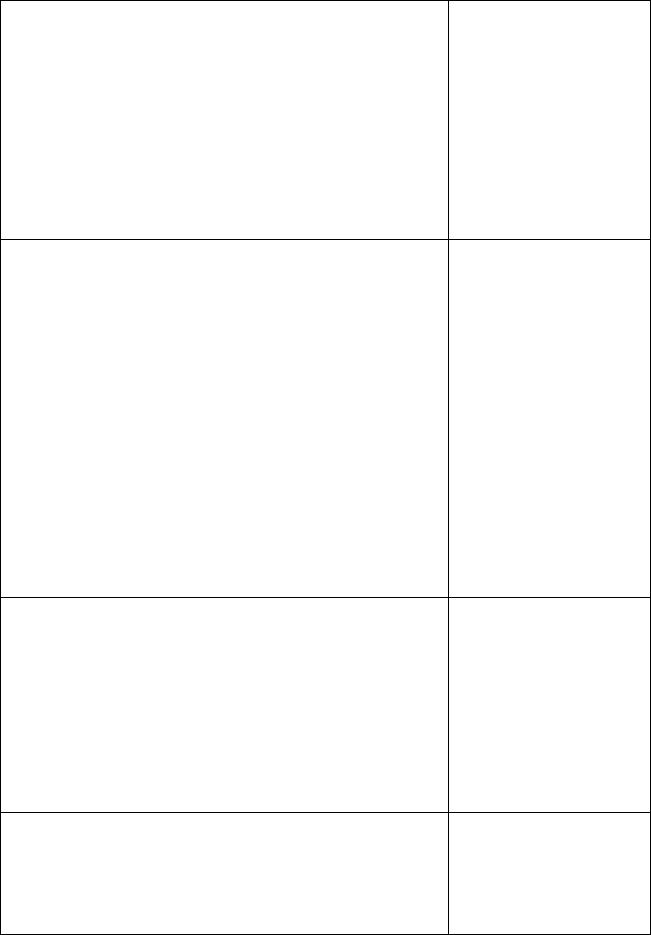
Оказывается, если на координатной плоскости изобразить графики этих решений при всевозможных А, то они покроют всю плоскость, причем через каждую точку плоскости пройдет в точности один из графиков. Плоскость оказывается как бы «сотканной» из графиков у=Аеkх (рис. 1).
Рис. 1
53
|
|
Докажем это, для чего найдём среди функций вида (4) все те, |
|
графики которых проходят через данную точку (х0, у0) |
|||
координатной плоскости. |
|
||
|
|
Для определения постоянной А получаем уравнение |
|
y |
0 |
Aekx0 , которое имеет единственное решение A y e kx0 . |
|
|
|
0 |
|
|
|
Следовательно, через нашу точку проходит один и только |
|
один из графиков (4) – это y y0e kx0 |
ekx , |
||
то есть y y0ek(x x0 ) |
(5) |
||
|
|
Полученный нами факт часто формулируют следующим |
|
образом: дифференциальное уравнение у = ky имеет единственное решение, удовлетворяющее начальному условию
у0 = у(х0), это решение задается формулой y y0ek(x x0 ) .
Более общее линейное дифференциальное уравнение записывается в виде у = ky + а (6) где а (как и k) – постоянная.
Уравнение (6) легко сводится к уже исследованному уравнению (2): если правую часть записать в виде
|
|
a |
|
|
|
|
|
|
|
|
|||
ky a k y |
|
|
(напомним, что мы считаем k≠ 0) и |
||||||||||
|
|||||||||||||
|
|
k |
|
|
|
|
a |
|
|
|
|||
обозначить функцию y |
через z, то y kz. С другой |
||||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
k |
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
a |
|
|
|
|
|
||||
стороны, z y |
|
|
|
y . Таким образом, z = kz. |
|||||||||
|
|||||||||||||
|
|
|
|
|
k |
|
|
|
|
|
|||
Итак, функция z(x) = y(x) + a/k удовлетворяет уравнению |
|||||||||||||
z = kz, поэтому z = Аеkх, |
то есть y |
a |
Aekx , откуда |
||||||||||
|
|||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
k |
||
y(x) |
Aekx |
|
|
|
(7) |
||||||||
|
|
|
|
||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
||
Значение постоянной опять-таки однозначно определяется, если задано начальное условие у0 = у(х0).
Определение. Линейное дифференциальное уравнение у = f(x,y) называется уравнением с разделяющимися переменными, если его можно представить в виде
у = f1(x) ∙ f2(у) (8)
где f1(x) и f2(у) – непрерывные функции.
Предположим, что f2(у) ≠ 0. Тогда уравнение (8) можно
записать так: |
|
dy |
|
f |
(x)dx. |
(9) |
||||
|
|
|
|
|||||||
|
|
f2(y) |
1 |
|
|
|
|
|||
Интегрируя уравнение (9), получим общее решение |
|
|||||||||
уравнения (8): |
|
|
dy |
|
|
f1(x)dx. |
|
|||
f |
2(y) |
|
|
|||||||
|
|
|
|
|
|
|||||
При решении дифференциальных уравнений с разделяющимися переменными можно использовать алгоритм:
1.разделить переменные;
2.интегрируя уравнение с разделёнными переменными, найти общее решение данного уравнения;
3.если заданы начальные условия, найти частное решение, удовлетворяющее данным условиям.
54
Пример. Решить уравнение 5х3-у′=0. |
|
|
|
|
||||||
Решение. Это дифференциальное уравнение с |
|
|
||||||||
разделяющимися переменными. Запишем его в следующем |
|
|||||||||
виде: |
у′ = –5х3. |
|
||||||||
Разделив переменные, получаем: |
dy =5x3dx. |
|
||||||||
Проинтегрируем полученное уравнение: dy 5 x3dx |
|
|||||||||
|
|
|
|
|
|
|
y 5 |
x4 |
C |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
5 |
|
4 |
|
|
|
Общее решение уравнения: y |
x4 C |
|
|
|
|
|||||
|
|
|
|
|
||||||
4 |
|
|
|
|
|
|||||
Ответ: y |
5 |
x4 C . |
|
|
|
|
||||
|
|
|
|
|
||||||
4 |
|
|
|
|
|
|
|
|||
3. Приложения линейных дифференциальных уравнений в естествознании |
||||||||||
Дифференциальные уравнения являются одним из самых |
В заключении, ребятам |
|||||||||
мощных средств математического решения практических задач. |
можно предложить |
|||||||||
Особенно широко они используются для решения задач |
продумать решение |
|||||||||
естественнонаучного цикла: физики, химии, биологии, |
следующей задачи. |
|||||||||
экологии. |
|
|
|
Определить наименьшую |
||||||
Рассмотрим процесс, исследование которого сводится к |
скорость, с которой нужно |
|||||||||
линейному дифференциальному уравнению, то есть к |
|
бросить тело вертикально |
||||||||
применению вышеизложенной теории. |
|
|
|
вверх, чтобы оно не |
||||||
М о д е л ь р о с т а п о п у л я ц и й |
б а к т е р и й . |
вернулось на Землю. |
||||||||
Пусть N(t) – численность размножающейся популяции |
Сопротивлением воздуха |
|||||||||
бактерий в момент времени t. При идеальных условиях |
пренебречь. |
|||||||||
приращение численности ∆N(t) = N(t + ∆t) – N(t) за время от t |
|
|||||||||
до t – ∆t для многих видов бактерий можно считать примерно |
|
|||||||||
пропорциональным количеству имеющихся в момент времени t |
|
|||||||||
бактерий; кроме того, при малых ∆t приращение ∆N(t) должно |
|
|||||||||
быть примерно пропорциональным ∆t. Таким образом, при |
|
|||||||||
сделанных допущениях можно записать |
∆N(t) ≈ k N(t) ∆t, где |
|
||||||||
k >0 – коэффициент, зависящий от вида бактерий. |
|
|
||||||||
Итак, |
N t |
kN(t). |
|
|
|
|
||||
|
|
|
|
|
||||||
|
t |
|
|
|
|
|||||
Отвлекаясь от того, что численность может измеряться |
|
|||||||||
только целыми числами, будем считать, что N(t) изменяется во |
|
|||||||||
времени непрерывно. Учитывая, что последнее равенство |
|
|||||||||
должно быть тем точнее, чем меньше ∆t, после перехода в нем |
|
|||||||||
к пределу при ∆t→0, получим дифференциальное уравнение |
|
|||||||||
вида (2): N (t) = kN(t). |
|
|
|
|
||||||
Следовательно, N(t)= Аеkt. Так что, численность популяции |
|
|||||||||
возрастает по показательному закону. Если при этом известна |
|
|||||||||
начальная численность популяции, то есть начальное условие |
|
|||||||||
N(0) = N0, то, следуя формуле (5), можно записать N(t)=No еkt. |
|
|||||||||
Рассмотрим конкретный пример. Определить во сколько раз |
|
|||||||||
увеличится количество бактерий за 9 часов, если в течение |
|
|||||||||
3 часов их количество изменилось от 100 до 200. |
|
|
||||||||
Решение. Как уже было сказано выше, скорость |
|
|
||||||||
размножения бактерий, если для них имеется достаточный |
|
|||||||||
запас пищи и созданы другие необходимые внешние условия |
|
|||||||||
(например, отсутствие подавления бактерий другими видами), |
|
|||||||||
пропорциональна их количеству. |
|
|
|
|
||||||
Пусть х – количество бактерий в данный момент, тогда |
|
|||||||||
55

скорость изменения их количества равна производной dx . dt
Так как скорость размножения бактерий пропорциональна
их количеству, то существует k, что dx kx. dt
Разделяем в дифференциальном уравнении переменные:
dx kdt . x
Интегрируя, получаем: |
|
dx |
kdt , |
|
|||
|
|
x |
|
ln x = kt + ln C,
что после потенцирования даёт e ln x = e , x = C ekt
Для нахождения С используем начальное условие: при t=0,
х=100. Имеем: Се0=100, С=100, и, значит, х=100ekt.
Коэффициент ek находим из условия: при t=3, х=200: 200 = 100e3k, 2 = e3k, 3
 2 3
2 3
 e3k , 3
e3k , 3
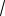 2 ek
2 ek
t
Искомая функция: x 100 23 . При t=9, х=800.
Ответ: количество бактерий за 9 часов увеличится в 8 раз.
Задание 2. Что бы вы изменили в содержании лекции? Ответ обоснуйте. Задание 3. В физико-математическом классе начать лекцию можно так:
«Математический анализ как анализ переменных величин с момента своего появления развивался в тесной связи с естествознанием, и в частности с физикой и механикой. Потребности развития физических наук, необходимости количественного изучения движения и меняющихся процессов, привели к возникновению и формированию основных понятий дифференциального исчисления и интегрального исчисления. Понятие дифференциального уравнения – одно из основных. Чтобы разъяснить это понятие, рассмотрим, из чего складывается изучение какого-либо физического процесса. Это – создание физической гипотезы, основанной на эксперименте, математическая форма записи физической гипотезы, математическое решение этой задачи и физическое толкование выводов из её решения. такой подход к изучению явлений природы впервые был предложен итальянским учёным Г. Галилеем. Впервые его блестяще применил один из создателей математического анализа И. Ньютон. Математически сформулировать физические законы оказалось возможным лишь с появлением математического анализа и на его языке.
В очень большом числе случаев физические законы описывают некоторые соотношения между величинами, характеризующими изучаемый процесс, и скоростью изменения этих величин. Другими словами, эти законы выражаются равенствами, в которых участвуют неизвестные функции и их производные. Такие равенства называются дифференциальными уравнениями».
Продолжите.
56

Тема 12. Измерение длин, углов, площадей и объёмов в ШКМ
I. Предваряющее задание: (1) Пропедевтика изучения темы (1-6 классы). (2) Как данная тема представлена в содержании ГИА (алгебра/геометрия) и ЕГЭ по математике. (3) Проанализируйте несколько уроков (Сайт ИД «1 сентября»), содержание которых составляют практические или прикладные задачи.
II.Практическая работа – 90 минут.
Задание 1. Проанализируйте текст творческой практической работы по теме «Объёмы тел».1
Объёмы тел
Содержание работы. Определите комфортность жилища, выясните наиболее комфортное жилище.
Оборудование: плакат с заданиями (табл.1), справочный материал «Площади плоских фигур», микрокалькулятор или программа Excel.
Порядок проведения работы.
1)Фронтальная работа: разделить учащихся на группы по 3-4 человека; ознакомить с обучающей программой, содержанием и порядком выполнения работы.
2)Самостоятельная работа по группам:
3)(а) Откройте файл «Комфортность жилищ», созданный в программе Excel.
(б) Составьте таблицу на экране компьютера согласно заданию.
|
(в) Вычислите коэффициент комфортности по формуле k |
36πV |
2 |
для каждого жилища. |
|||||||
|
S3 |
|
|||||||||
|
(г) Внесите полученные результаты в таблицу по графам. |
|
|
|
|||||||
|
|
|
|
|
|||||||
|
(д) Сделайте вывод о наиболее комфортном жилище. |
|
|
|
|
||||||
|
|
4) Оформление работы. |
|
|
|
|
|
|
|
|
|
|
Группа № ___ Ф.И.учащихся _________________________ |
|
5) Распечатайте результаты работы |
||||||||
|
__________________________________________________ |
|
|||||||||
|
|
|
|
|
|
|
|
группы. |
|
|
|
|
|
|
|
|
Таблица 1 |
|
|
|
|||
|
№ |
|
Название жилища |
V |
S |
k |
|
6) Обсуждение результатов |
|||
|
|
|
|
|
|
|
|
исследования и оценка работы. |
|||
|
|
|
|
|
|
|
|
Критерии оценки: |
|||
|
|
|
|
|
|
|
|
1. |
Самостоятельно поставил цель |
||
|
|
|
|
|
|
|
|
исследования. |
|||
|
|
|
|
|
|
|
|
2. |
Самостоятельно составил план |
||
|
Вывод. |
|
|
|
|
выполнения задания. |
|||||
|
|
|
|
|
|
|
|
3. |
Самостоятельно нашёл метод |
||
|
|
|
|
|
|
|
|
решения задачи. |
|||
|
|
|
|
|
|
|
|
||||
4.Могу объяснить ход выполнения вычислений и сделанный вывод.
5.Могу обосновать предложенное решение задачи.
6.Могу предложить рациональный способ решения задачи.
7.Могу составить новую задачу по данным исходной задачи.
8.Самостоятельно оцениваю результаты своей познавательной деятельности.
7)Домашнее задание. Определите коэффициент комфортности собственной комнаты, квартиры, других помещений.
Задание 2. Разработайте творческую практическую работу по теме «Площади фигур».
1 Тараник В.И. Самостоятельная познавательная деятельность учащихся и её развитие средствами практических работ по геометрии: учеб.-метод. пособие / науч. редактор В.А. Далингер. – Омск: ООО ИПЦ «Сфера», 2009. –
С.170-171.
57

Задание 3. Охарактеризуйте практические работы из заданий 1 и 2, используя классификации, представленные в материалах темы 8.
Задание 4. Проанализируйте урок.
Понятие объема. Объем прямоугольного параллелепипеда. 11-й класс http://festival.1september.ru/articles/413657/
Цель урока: Ввести понятие объема тела, рассмотреть свойства объемов, теорему об объеме прямоугольного параллелепипеда и следствие об объеме прямой призмы, основанием которой является прямоугольный треугольник.
ХОД УРОКА
I. Понятие объема тела
– Величина части пространства, занимаемого геометрическим телом называется объемом этого тела.
II. Рассказ учителя о мерах объема
II.1. В повседневной жизни нам часто приходится определять объемы различных тел. Например, коробки, банки. В житейской практике единицами объема служили меры емкости, используемые для хранения сыпучих и жидких тел.
Среди них английские меры: Бушель – 36,4 дм3 Галлон – 4,5 дм3
Баррель (сухой) – 115,628 дм3 Баррель (нефтяной) – 158,988 дм3
Английский баррель для сыпучих веществ 163,65 дм3. Меры когда-то, применявшиеся в России:
Ведро – 12 дм3 Бочка – 490 дм3
Штоф – 1,23 дм3 = 10 чарок Чарка – 0,123 дм3=0,1 штофа = 2 шкалика Шкалик – 0,06 дм3 = 0,5 чарки.
II.2. Поиск формул, позволяющих вычислять объемы различных тел, был долог.
В древнеегипетских папирусах, в вавилонских клинописных табличках встречаются правила для нахождения объема усеченной пирамиды, но не сообщаются правила для вычисления объема полной пирамиды.
Определять объемы призмы, пирамиды, цилиндра и конуса умели древние греки еще задолго до Архимеда. Но только он имел общий метод, позволяющий определить любую площадь или объем. Идеи Архимеда легли в основу интегрального исчисления. Сам ученый определил с помощью своего метода площади объемы почти всех тел, которые рассматривались в античной математике.
На могильной плите Архимеда, как завещал ученый, был изображен цилиндр с вписанным шаром, а эпитафия говорила о величайшем открытии Архимеда – о том, что объемы этих тел относятся как 3 : 2.
Когда Римский оратор и общественный деятель Цицерон, живший в 1 в. до н.э., был в Сицилии, он еще видел этот заросший кустами и терновником памятник с шаром и цилиндром.
58

III. Постановка задачи
–Наша задача на уроке – найти для объема выражение
ввиде некоторого числа, измеряющего эту величину. При этом мы будем руководствоваться следующими исходными положениями:
Равные тела имеют равные объемы. (Понятие определяется на основе понятия наложения).
Объем тела, состоящего из некоторых частей, равен сумме объемов этих частей.
IV. Объяснение нового материала
– Процедура измерения объемов аналогична процедуре измерения площадей. Число измерения (единичных кубов) и частей единицы, содержащихся в данном теле, принимается за числовое значение объема при выбранной единице измерения. Это число может быть как рациональным (в частности, целым), так и иррациональным.
– Доказать важное следствие: Объем куба с ребром 1
ï
1
равен .
ï 3
– Доказать теорему об объеме прямоугольного параллелепипеда.
Дано: параллелепипед, а, b, c его измерения, V – объем параллелепипеда.
Доказать: V = abc. Доказательство:
1. Пусть а, b, c – конечные десятичные дроби (n > 1). Числа а 10n , b 10n, c 10n – целые.
Разобьем каждое ребро параллелепипеда на равные части
длины |
1 |
и через точки разбиения проведем плоскости, |
|
||
10ï |
|
|
перпендикулярные к этому ребру.
Параллелепипед разобьется на abc∙103n равных кубов с
ребром |
1 |
. |
|
|
|
|
|
|
|
|
|
||||
10ï |
|
1 |
|
|
|
||
Т.к. объем каждого такого куба равен |
, |
то объем |
|||||
|
|||||||
|
|
103ï |
|
1 |
|
||
всего параллелепипеда равен V abc 103n |
. |
||||||
|
|||||||
|
|
|
|
103ï |
|
||
Итак, V = abc.
2. Хотя бы одно из измерений a, b, c – бесконечная десятичная дробь. Пусть аn, bn, cn – конечные десятичные дроби, полученные из чисел a, b, c отбрасыванием в каждом из них всех цифр после запятой, начиная с (n + 1)
|
àï |
|
|
1 |
(аналогично |
|
10ï |
||||||
цифры. Тогда an < a < an , где àï |
||||||
для b, c). Перемножим эти неравенства anbncn < abc < an bn cn .
По доказанному в п. 1., левая часть – Vn, а правая Vn . Т.к. параллелепипед Р содержит в себе параллелепипед Рn, а сам содержится в параллелепипеде Pn , то объем V параллелепипеда Р заключен между Vn = anbncn и
59

Vn = an bn cn |
т.е. anbncn < V < an bn cn . |
|
|
При неограниченном увеличении n число |
1 |
будет |
|
|
|||
|
10ï |
|
|
становиться сколь угодно малым, и потому числа anbncn и an bn cn будут сколь угодно мало отличаться друг от друга. Следовательно, число V сколь угодно мало отличается от числа abc. Значит они равны: V = abc. Ч.т.д.
V. Закрепление
Рассмотреть следствие 1. Объем прямоугольного параллелепипеда, равен произведению площади основания на высоту.
Доказать следствие 2. Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.
VI. Решение задач № 650. № 653 (Уч. Атанасян Л.С. и др. Геометрия 10–11)
VII. Итог урока
VIII. Домашнее задание п.63 п.64. №654, № 656 (Уч. Атанасян Л.С. и др. Геометрия 10–11)
ВЫВОДЫ.
III.Внеаудиторное задание.
(1)Составьте и заполните диагностическую карту по теме Площадь треугольника.
(2)Проведите анализ урока «Правильные многоугольники» – http://festival.1september.ru/articles/522424/.
(3)Разработайте ЦОР по теме «Углы. Вычисление углов».
(4)Как можно применить технологию «полного усвоения» к изучению материала темы «Измерение длин, углов, площадей и объёмов»?
(5)Используя возможности интерактивной творческой среды «1С: Математический конструктор», разработайте расширяющееся задание по теме занятия.
(6)Подготовьте аннотированный библиографический список по теме.
(7)Какие занимательные задания по теме Вам известны. Каким образом эти задания можно использовать в учебном процессе?
(8) Охарактеризуйте современные подходы к изучению величин в начальном курсе математики.
60
