1.9. Дополнительные задачи к Части 1: уравнения Лагранжа и Клеро.

Общие сведения. Дифференциальные уравнения Лагранжа и Клеро есть частные (специальные) случаи уравнений, не разрешённых относительно производной. Дифференциальное уравнение 1-го порядка называют уравнением Лагранжа, если его запись имеет вид:. В случае, когда , уравнение Лагранжа классифицируется как уравнение Клеро. Решения уравнений Лагранжа и Клеро ищутв параметрической форме.

Задача: Имеем дифференциальное уравнение:. Отметить, что заданное уравнение является уравнением Лагранжа и решить его, применив стандартный алгоритм решения.

Общая схема решения задачи:

1). Примем: = и запишем для функции параметрическое выражение: .

2). Исследуем разность: . Если возможно: =0, записываем одно из решений уравнения: =+, которое может оказаться особым.

3). Составим линейное уравнение: –=. Применяя стандартный алгоритм решения линейного уравнения, получим его общее решение: .

4). Запишем общее решение уравнения в параметрической форме: Возможна запись общего решения в виде: .

5). Если решение: =+ не получается из общего решения: ни при каком значении произвольной постоянной величины, объявить это решение особым.

6). Если заданы начальные условия: , выделяем из общего решения соответствующее частное решение.

7). Оформляем результат решения задачи – записываем Ответ.

Пример (и образец оформления):

Пример 1.9. Найти общее решение уравнения Лагранжа: в параметрической форме.

Решение:

1. Форма записи уравнения имеет вид: , где=и=0. Примем:=, то есть. Перепишем исходное уравнение:=.

2. Дифференцируем по переменной:. Учитывая=, запишем:. В нашем случае:=и=0, также= .

3. Исследуем равенство: =0. Его решения в нашем случае:=–1 и=1. Учитывая, запишем:

а) для =–1:→=;

б) для =1:→=.

4. Теперь . Учитывая=, перепишем:в виде линейного уравнения:–=. В нашем случае имеем:= – уравнение с разделяющимися переменными, откуда.

5. Составим систему: или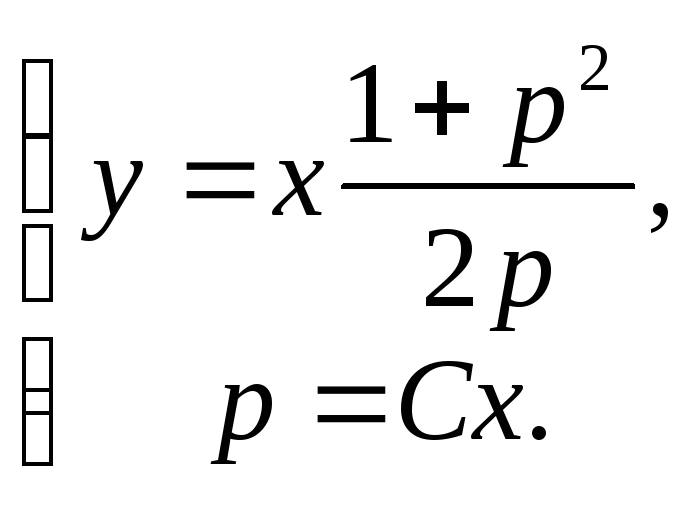– решение уравнения Лагранжа в параметрической форме, что легко приводится к виду:– общее решение.

Ответ: – общее решение в параметрической форме, или . Особые решения уравнения: (из общего решения не получаются ни при каком ).

Задание 1.9. Решить уравнение Лагранжа:

Вар.	Уравнение:	Вар.	Уравнение:
1.9.1.		1.9.4.
1.9.2.		1.9.5.
1.9.3.		1.9.6.

Задача: Имеем дифференциальное уравнение:. Отметить, что заданное уравнение является уравнением Клеро и решить его, применив стандартный алгоритм решения.

Замечание: В теории дифференциальных уравнений уравнения Клеро занимают особое место. Наряду с оригинальностью общего алгоритма решения уравнений Клеро, их изучение требует применения таких важных понятий, как семейство кривых линий, огибающая семейства кривых. Понятие особые решения дифференциальных уравнений наиболее выразительно иллюстрируется при изучении уравнений Клеро!..

Общая схема решения задачи:

1). Примем: = и запишем общее решение уравнения Клеро: – семейство прямых линий.

2). Запишем систему, определяющую огибающую семейства прямых линий – особое решение уравнения Клеро:

общая запись: для уравнения Клеро:

3). Если заданы начальные условия: , выделяем из общего решения соответствующее частное решение.

4). Оформляем результат решения задачи – записываем Ответ.

Пример (и образец оформления):

Пример 1.10. Решить уравнение Клеро: , применяя метод введения параметра.

Решение:

1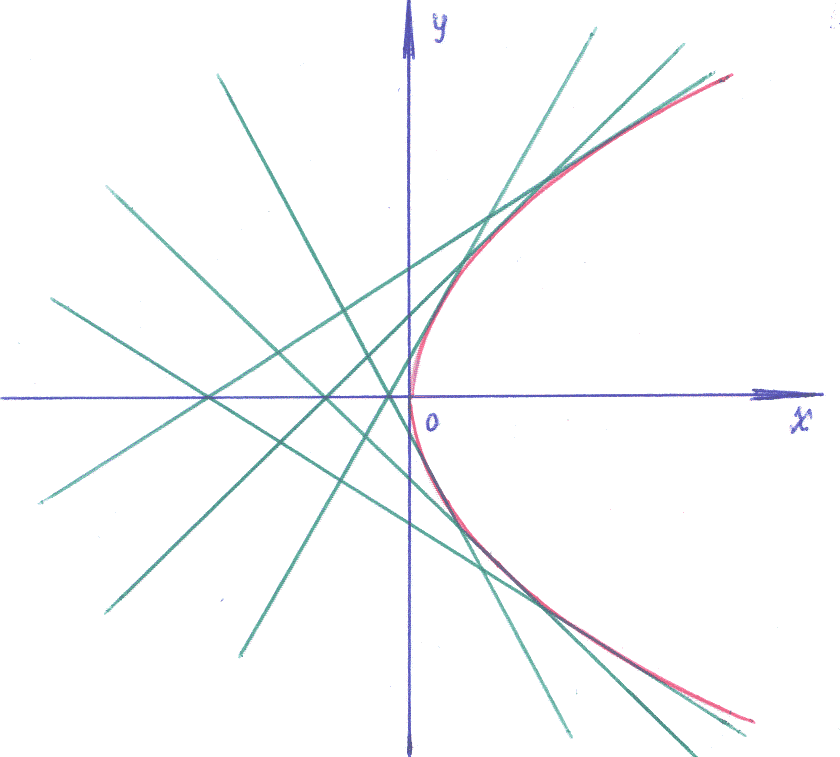). Анализируя форму записи заданного уравнения, замечаем, что это уравнение Клеро. Применив подстановку=, получаем выражение: ,которое является общим решением заданного уравнения:

2). Из общей записи системы: для поиска огибающей семейства кривых линий:=0 получаем систему, которая определяет особого решения заданного уравнения:илив параметрическом виде. В данном случае нетрудно перейти от параметрической формы записи особого решения (огибающей семейства прямых линий, соответствующего общему решению уравнения) к форме: – парабола.

Ответ: общее решение: , особое решение: – парабола (огибающая).

Задание 1.10. Решить уравнение Клеро:

Вар.	Уравнение:	Вар.	Уравнение:
1.10.1.		1.10.4.
1.10.2.		1.10.5.
1.10.3.		1.10.6.

Замечание: При выборе Заданий с уравнениями Лагранжа и Клеро поступаем так: Задание №1 выполняют студенты, у которых порядковые номера в Списке группы: 1-7-13-19-25; Задание №2 выполняют, соответственно, те, у которых номера в Списке: 2-8-14-20-26 и так далее... В образующихся коллективах студентов может применяться самое активное сотрудничество!..

• ◄ ≡ ► •