§7. Множество мощности континуума

Теорема 1.Множество натуральных чиселNи множество действительных чиселRнеравномощны.

Доказательство:

I. Так какR, то достаточно доказать несчётность интервала.

Задача:показать, что не существует биективного отображенияN.

Приведём знаменитое доказательство Кантора, которое он сообщил в 1891 году на съезде естествоиспытателей в Галле.

1. Все действительные числа будем записывать в виде бесконечных десятичных дробей. Для устранения неоднозначности записи некоторых из них конечные десятичные дроби будем представлять в виде бесконечных с периодом 9.

2. Предположим, что множество точек интервала 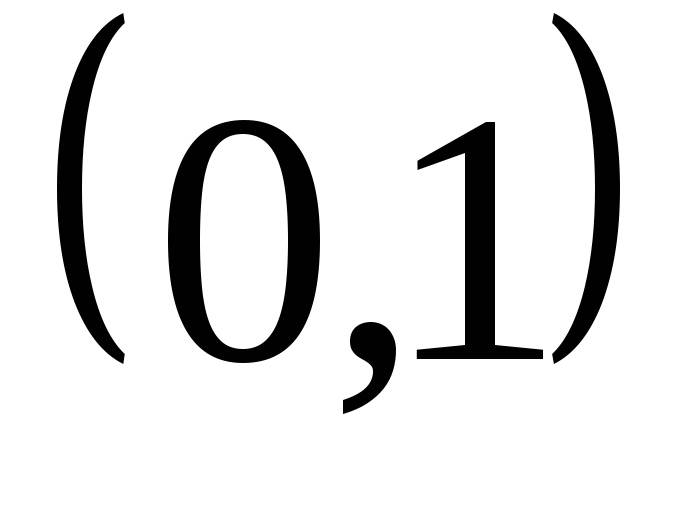счётно, то есть всех их можно занумеровать: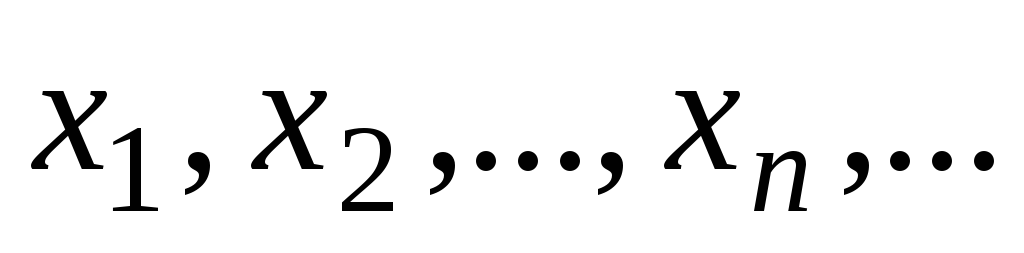. Каждое такое число – бесконечная десятичная дробь:

.

3. Образуем десятичную дробь , отличную от всех чисел этого множества:

,

выбирая числа , отличные от «диагональных»:

,

,

………………….

,

………………….,

но так, чтобы все и(то есть, чтобыи). Ясно, что такой выбор возможен.

4. Очевидно, что .

5. Если предположение о счётности дробей интервала верно, тоN, такой что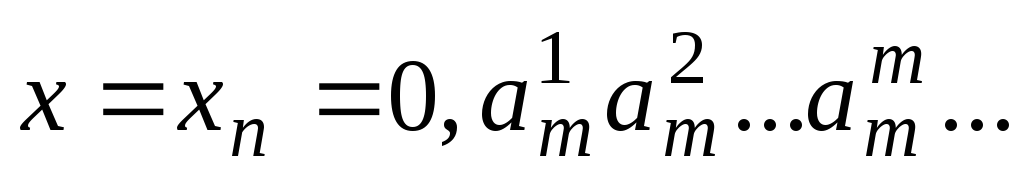, откуда следует равенство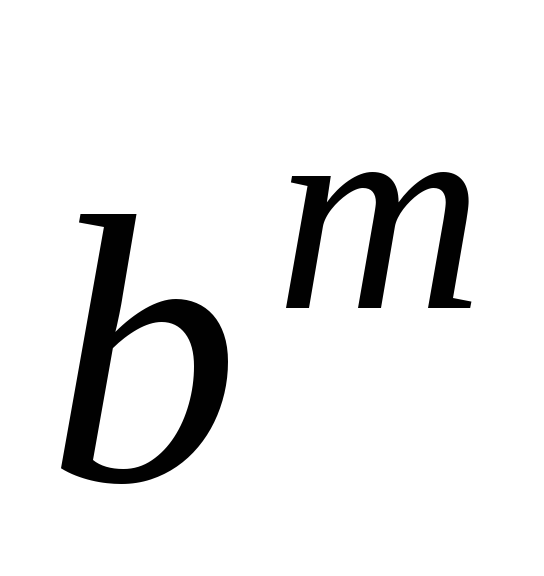некоторому «диагональному элементу»: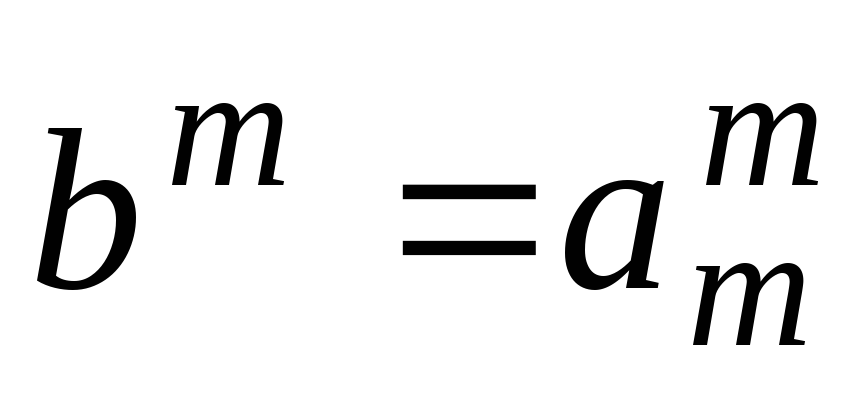, что противоречит выбору числа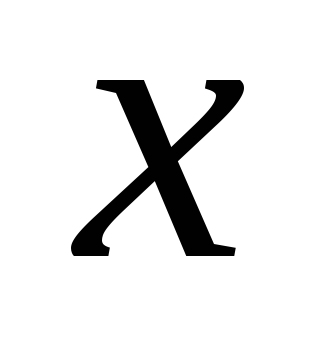. Следовательно, десятичная дробь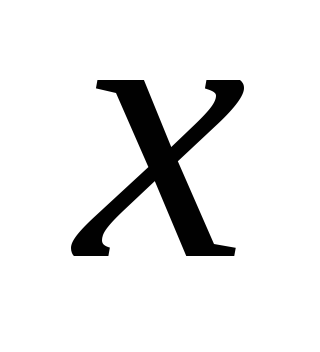, определённая выше, не входит в счётное множеств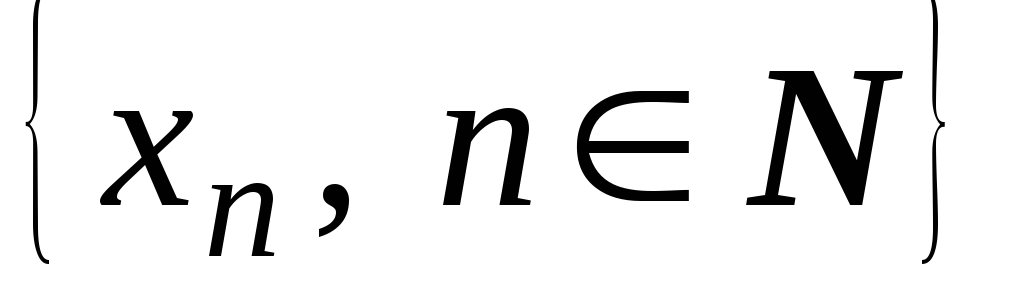о, но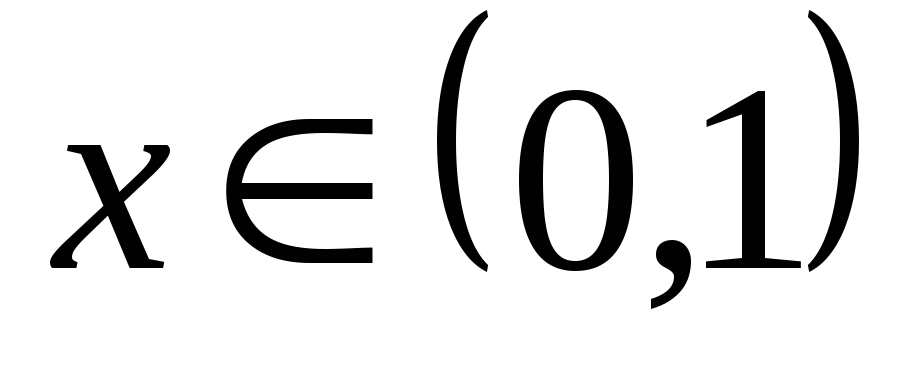. Итак, все числа интервала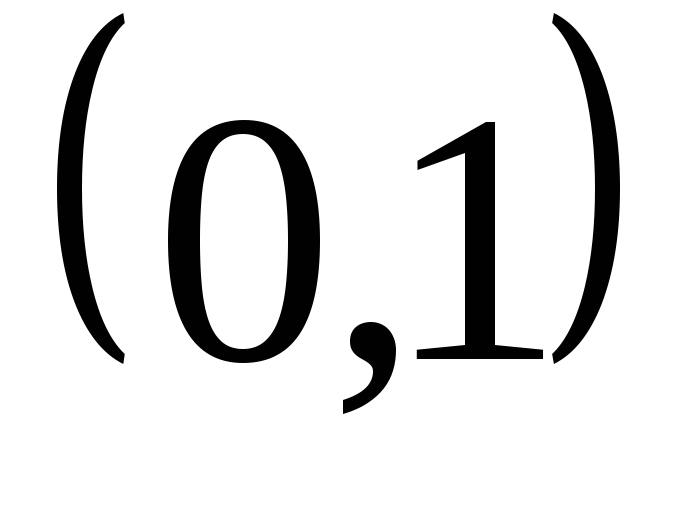занумеровать нельзя, то есть не существует биективного отображенияNв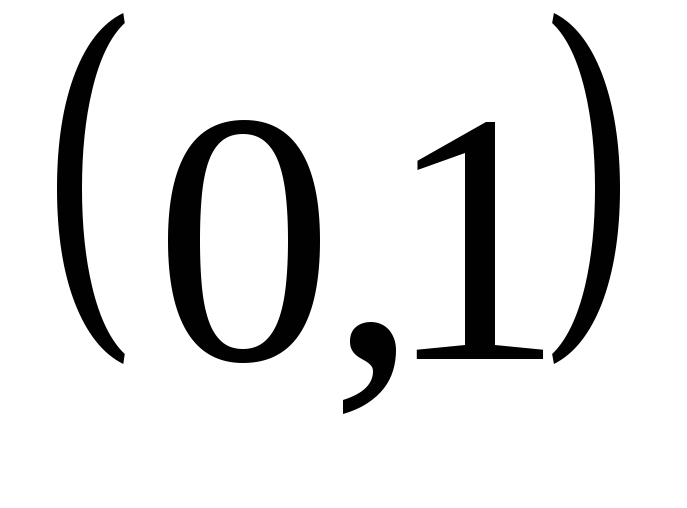, и множество точек такого интервала несчётно.

II. Пустьf- произвольное отображение изNвR:f: NR.Обозначим черезВ образ множестваNпри отображенииf, то естьВ=f(N)={f(1),f(2),…,f(n),…}={f(n)}. Рассмотрим отрезок. Разобьём его точками на три равных отрезка. По крайней мере, один из отрезков не содержитf(1). Обозначим его через. Еслиf(1)не принадлежит ни одному из отрезков, то в качествевыбираем произвольный. Далее делим отрезокна три равные части и черезобозначаем тот отрезок, который не содержитf(2)и так далее. Продолжая этот процесс неограниченно, получим последовательность вложенных отрезков:

. (1)

Последовательность отрезков (1) является стягивающейся. По теореме Кантора существует единственная точка с, принадлежащая всем отрезкам данной последовательности, то есть

.

Так как , а, то, то есть, но. Значит существует действительное число, не являющееся образом никакого натурального числа при отображенииf, следовательно,fбиекцией не является,Nне равномощноR.

Так как Nсчётно, тоRнесчётно. Так как, то. Так какNне равномощноR,.

Определение 5. Множество R называется числовым континуумом. Множество, равномощное множеству R называется множеством мощности континуума.

Мощность континуума обозначается с.

Примеры множеств мощности континуум

1. Все промежутки;

2. Множество иррациональных чисел I:,Rнесчётно,Qсчётно, по теореме 11, то есть;

3. Множество трансцендентных чисел Т:,Rнесчётно,Асчётно, по теореме 11, то есть.

Основные свойства множеств мощности континуум

Теорема 2. Декартово произведение счётной совокупности счётных множеств имеет мощность континуум.

Теорема 3. Декартово произведение счётной совокупности конечных множеств, каждое из которых имеет не менее двух элементов, имеет мощность континуум.

Теорема 4. Объединение конечной или счётной совокупности множеств мощности континуум имеет мощность континуум.

Теорема 5. Декартово произведение конечной или счётной совокупности множеств мощности континуум имеет мощность континуума.