Примеры эквивалентных множеств

Если множества состоят из конечного числа элементов, то сравнить их, то есть установить, существует ли биективное отображение одного в другое, не составляет большого труда. Однако для множеств, число элементов которых бесконечно, задача отыскания такого отображения непроста даже в очевидных случаях.

Пример 1.Пусть- множества точек на двух параллельных сторонах прямоугольника. Тогда.

П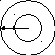ример 2.Пусть- множества точек двух концентрических окружностей. Тогда.

Пример 2 уже не так тривиален, как пример 1: если «распрямить» обе окружности, то одна из них буде короче другой, и, казалось бы, что на ней точек «меньше». Однако, это не так.

Пример 3.ПустьА- множество точек гипотенузы, аВ– множество точек катета прямоугольного треугольника. Тогда, хотя катет короче гипотенузы. Если наложить катет на гипотенузу, то множествоВокажется собственным подмножеством множестваА.

Пример 4.Ответим на вопрос: каких чисел больше: натуральных или чётных положительных? Казалось бы, ответ очевиден:2NN, то есть чётных натуральных чисел «меньше», чем натуральных. Однако эти множества равномощны. Действительно,

N,2N.

1. это отображение, так как каждому элементу первого множества соответствует единственный элемент второго множества;

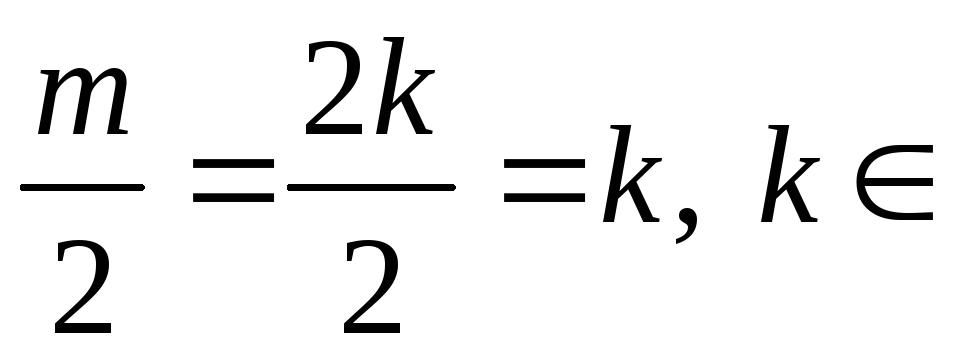2. отображение сюрьективно, так как 2N (для любого элемента, то есть для любого чётного числа есть прообраз во множестве натуральных чисел N).

3. отображение инъективно, так как

N, .

Из 1)-3) следует, что отображение биективно.

В примерах 2-4 содержится один из парадоксов бесконечных множеств: бесконечное множество может быть равномощно своему собственному подмножеству. Этот парадокс во время создания теории множеств ставил в тупик многих математиков. Например, Больцано (чешский математик, 1781-1848) в связи с этим парадоксом отказался от взаимной однозначности как от критерия равномощности и, таким образом, остался вне основной линии развития теории множеств.

Ясно, что конечное множество не имеет равномощных ему собственных подмножеств. Этим свойством обладают именно бесконечные множества. Исходя из этого можно дать строгое определение конечных и бесконечных множеств.

Определение 2 (Дедекинд).Множество называетсябесконечным,если в нём имеется собственное подмножество, равномощное данному множеству. В противном случае множество называетсяконечным.

Пример 5. Все отрезки равномощны.

Пример 6. Все интервалы равномощны.

Пример 7.Множества точек полуокружности и её диаметра (общие, диаметрально противоположные точки выколоты) равномощны.

Пример 8.Множества точек прямой и касающейся её полуокружности без диаметрально противо-положных точек равномощны.

Пример 9.Множества точек прямой и любого её интервала (примеры 7+8).

Упражнение. Привести «геометрические» доказательства примеров 5-9.

Пример 10.ПустьZ₀=N. Докажем, чтоZ₀ ~N. Зададим отображение формулой

Z₀.

Очевидно, что fсюрьективно и инъективно, а следовательно, и биективно.

В примере 10 к множеству натуральных чисел добавили один элемент и получили равномощное ему множество. Этот факт можно обобщить на любое бесконечное множество.

Теорема 1. Если к бесконечному множествуАдобавить один элемента, то получим множествоВ, равномощное данному.

Доказательство:

По условию . Докажем, что. Так какА- бесконечное множество, то из него можно выделить последовательность элементов

,

где все элементы попарно различны. Последовательность – функция натурального аргумента. Следовательно,А₀N.Обозначим . Построим отображение изZ₀по закону: N ,. Отображение- биекция, следовательно,В₀  Z₀илиZ₀ ~ В₀.Таким образом,А₀  N, N Z₀(пример 10), B₀  Z₀. Следовательно, A₀  B₀, то есть междуA₀и B₀существует биекция. Обозначим еёh:

.

Пусть далее . Тогда ,и .Зададим отображение изАвВследующим образом:

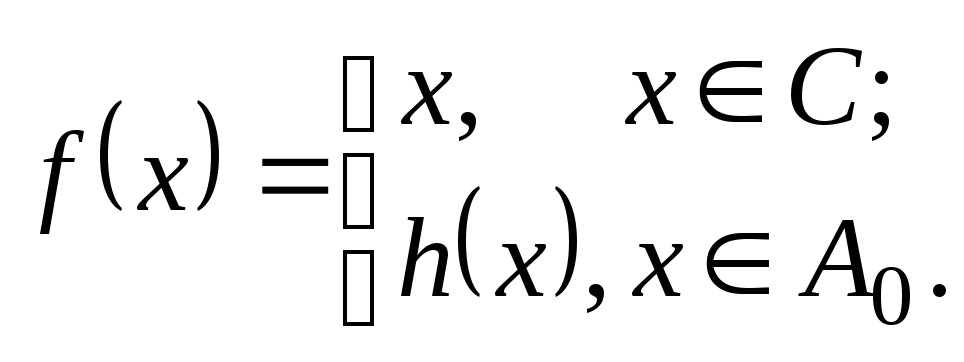
Отображение fбиективно. Следовательно,.

Следствие.Все промежутки (отрезки, интервалы, полуинтервалы) равномощны.

Покажем, например, что . Действительно,

.

Пример 11. Понятно, что точек как на прямой, так и на плоскости бесконечно много. Но где «больше»? Приведём рассуждения Кантора по этому поводу.

1. Способом, аналогичным доказательству равномощности прямой и интервала, можно показать равномощность множеств точек плоскости и квадрата без ограничивающих его отрезков. Это сводит задачу сравнения мощностей прямой и плоскости к сравнению равномощных им множеств точек интервала и квадрата.

2. Множество точек квадрата естественным образом отождествимо с множеством пар ,где- бесконечные десятичные дроби вида, которые предполагаются записанными в бесконечном виде, то есть исключается запись дробей с конечным числом значащих цифр. Это возможно сделать, т.к. всякую конечную десятичную дробь можно представить в виде бесконечной с периодом 9. Будем рассматривать такую запись во избежание неоднозначности.

Идея Кантора заключалась в том, чтобы слить эти дроби в одну десятичную дробь, по которой однозначно восстанавливались бы (инъекция) и которая принимала бы все положительные значения, не превосходящие единицы (сюрьекция), по одному разу (отображение), когда точкапробегает по всему квадрату (область определения). Тем самым было бы получено биективное отображение квадрата без границ на единичный интервал.

Первая попытка.

Казалось бы такое соответствие просто установить, положив

.

Проверим, является ли fбиективным отображением:

а) Так как парой однозначно определяется число, то указанное соответствие является отображением.

б) По дроби , отделяя числа на чётных и нечётных местах после запятой, можно восстановитьиоднозначно, что означает инъективность отображения.

3) Однако, оказывается, что такое отображение не сюрьективно, так как существуют бесконечные десятичные дроби, например, дроби вида , которые получаются только из конечных дробей (в данном случае- конечная десятичная дробь), а конечные дроби для однозначной записи чисел мы исключили из рассмотрения.

Вторая попытка.

Обойти это противоречие можно, взяв в качестве не отдельные цифры, а «молекулы десятичные дроби» (по Кантору), соединяя в одно целое любую ненулевую значащую цифру с предшествующими нулями. Например, если

, то.

Изменим правило: пусть теперь означают теперь не цифры, стоящие соответственно на нечётных и чётных местах после запятой, а такие «молекулы». Тогда любой пареоднозначно соответствует бесконечная дробьz, которая в свою очередь однозначно определяет ихиy, распадаясь на две дроби с бесконечным числом «молекул», то есть на бесконечные десятичные дроби. Такое отображение инъективно, то есть пох иyможет возникнуть только однажды.

Это биективное отображение и устанавливает равномощность квадрата и интервала, что в конечном счёте приводит к утверждению, что плоскость и прямая имеют одинаковую мощность. Итак,

R² ~ R.

Обобщение этого доказательства на произвольную степень Rⁿвполне очевидно. Интересно, что Кантор с 1874 года пытался доказать невозможность биективного отображения между множествамиRⁿиRпри, пока он к своему удивлению не построил его.«Я это вижу, но не верю в это», - писал он Дедекинду.

Пример 12. Множество натуральных чисел равномощно множеству рациональных чисел:

N ~ Q.

Любое рациональное число, не равное нулю, однозначно записывается в виде несократимой дроби , где. Из возможных записей для нуля выберем одну, например,. Тогда запись видаоднозначно определена для всех рациональных чисел (в частности, приполучаются все целые числа). Высотой числаназовём натуральное число, тогда все рациональные числа можно расположить в одну последовательность в порядке возрастания высоты, а числа с одинаковой высотой - в порядке возрастания числителя. Таким образом, получим последовательность

Так как чисел данной высоты hлишь конечное число (а именно, не более2(h-1)+1, так как числитель меняется от–(h-1)до(h-1)), то перед каждым фиксированным числом в последовательности стоит лишь конечное число чисел, следовательно, нумеруя числа последовательности по порядку натуральными числами, мы занумеруем все рациональные числа.