§5. Сравнение мощностей множеств

Теорема 1 (о мощности промежуточного множества).ЕслиА₂А₁А и А₂А А₁А (А₂А₁).

Доказательство:

Так как А₂А, то между этими множествами можно установить взаимно однозначное соответствие. Пусть по принятому закону соответствия собственному подмножествуА₁множестваАбудет соответствовать некоторое собственное подмножество множестваА₂, которое обозначимА₃. Итак,

А₂А, А₁А₃,, гдеА₃А₂.

Далее по тому же закону соответствия множеству А₂А₁будет соответствовать некоторое собственное подмножествоА₄А₃, то есть

А₂А₄,А₄А₃.

Продолжая этот процесс неограниченно, получим последовательность убывающих множеств

АА₁А₂…А_n…,

таких, что каждое последующее множество является собственным подмножеством предыдущего и

АА₂,

А₁А₃,

А₂А₄,

…

А_nА_n+2….

Кроме того, в силу принятого закона соответствия

А\А₁  А₂\А₃,

А₁\А₂  А₃\А₄,

А₂\А₃  А₄\А₅, (1)

…

А_n\А_n+1  А_n+2\А_n+3….

Действительно, nNпо принятому закону взаимно-однозначного соответствия элементов множестваА_nи элементов множестваА_n+2, элементы множестваА_n+1, составляющие собственное подмножество множестваА_n, ставятся в соответствие элементам множестваА_n+3, являющегося собственным подмножеством множестваА_n+2. Следовательно, и элементы оставшихся частей множествА_nиА_n+2 после удаления из них соответствующих множествА_n+1иА_n+3 оказываются поставленными во взаимно однозначное соответствие. Пусть далее

.

Множества АиА₁ можно представить в виде объединения попарно непересекающихся множеств:

,

.

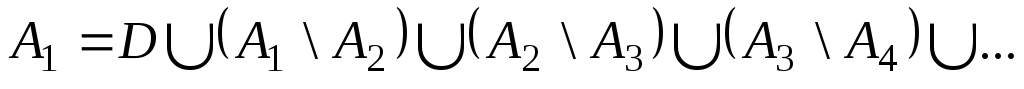Слагаемые первой строки либо совпадают с соответствующими слагаемыми второй, либо равномощны им на основании (1). Следовательно, АА₁.

Замечание.В общем случае изАА₂ иА₁А₃ не следует, чтоА\А₁  А₂\А₃. Например, пустьА=N,А₂=2N,А₁=2N,А₃=2N. ТогдаАА₂, А₁А₃, ноА\А₁=2n-1, n3, nN -бесконечное множество, аА₂\А₃= . Следовательно, множестваА\А₁ и А₂\А₃ не равномощны.

Теорема 2 (Кантора-Бернштейна). Если каждое из двух данных множеств равномощно некоторой части другого, то они равномощны:

АВ₁В, ВА₁А  АВ.

Доказательство:

Подмножества А₁иВ₁предполагаем собственными, так как в ином случае справедливость теоремы очевидна: еслиА₁=А, тоАВ₁В, ВАА  АВ.

Так как АВ₁, то элементы множестваАможно поставить по некоторому закону во взаимно-однозначное соответствие с элементами множестваВ₁. Обозначим черезВ₂собственное подмножество множестваВ₁, которое составлено из элементов, соответствующих по принятому закону элементам множестваА₁. Тогда

ВА₁, А₁В₂  ВВ₂.

Но

В₂В₁ВиВВ₂.

По теореме 1 ВВ₁или В₁В. Итак,АВ₁, В₁В. Следовательно,АВ.

Пусть Аи В - произвольные множества,m(А)=, m(В)=. Возможны следующие случаи:

1. А;

2. АиВ не равномощны, но вАесть подмножество, равномощноеВ, то естьВА₁А;

3. АиВне равномощны, ноА В₁В;

4. АВ₁В,ВА₁А;

5. В А нет части, равномощнойВ и вВнет части, равномощнойА.

Для конечных множеств АиВвозможны случаи 1-3, невозможны случаи 4,5. Для бесконечных множеств невозможен случай 5, а в случае 4 по теореме Кантора-Бернштейна множества равномощны, то есть случай 4 совпадает со случаем 1. Итак, для любых множествАиВ возможны только три случая 1-3.

Определение 1.Если для множеств АиВимеет место случай 1, тоm(А)=m(В).

Если для множеств АиВимеет место случай 2, тоm(А)m(В).

Если для множеств АиВимеет место случай 3, тоm(А)m(В).

Так как для любых множеств АиВосуществляется один и только один из трёх случаев 1-3,то для их мощностей возможно только одно из соотношений:

= > <.

Если А, тоm(А)m(В). Из теоремы Кантора-Бернштейна следуетчто еслиm(А)m(В)иm(В)m(А),тоm(А)=m(В).