§ 5. Бесконечно большие последовательности (ббп)

Определение 1. Последовательность называется бесконечно большой, если выполняется .

Для обозначения ББП используется запись .

Замечание 1. ББП не является сходящейся и запись не означает, что последовательность имеет предел. Это только обозначение ББП.

Геометрический смысл определения ББП

Геометрически определение ББП означает, что в любой (сколь угодно большой) окрестности нуля находится лишь конечное число членов ББП, а вне ее – все члены последовательности, начиная с некоторого номера(или, другими словами, все члены, начиная с некоторого номера, находятся в окрестности точки ∞) .

Замечание 2. Всякая ББП является неограниченной, так как вне любой окрестности нуля имеется член этой последовательности (даже все члены, начиная с некоторого).

Обратное утверждение не верно:

если - неограниченная последовательность, то , для которого выполняется, (1)

если -ББП, то выполняется (2)

Отсюда видно, что из (2)(1), а из (1) не следует(2).

Пример 1. Доказать, что - ББП.

∆выполнено .

Возьмем (сколь угодно большое) и найдем номерN, начиная с которого . Ясно, что надо взять, тогда дляn=N+1, N+2, и т.д. n>M   .∆

Определение 2. Последовательность называется бесконечно большой положительной, если выполняется .

Обозначается .

Определение 3. Последовательность называется бесконечно большой отрицательной, если выполняется .

Обозначается .

Например, .

Теорема 1. 1) Если - ББП, причем , то- БМП,

2) если - БМП и , то-ББП.

Доказательство.

1) Пусть . Возьмем и положим.

Тогда по определению ББП для выбранного  выполняется .

2) Доказательство аналогично.

Пример 2. Доказать, что .

∆ выполняется .

Возьмем , тогда, начиная с номеравыполнено.∆

§ 6. Свойства пределов, связанные с арифметическими операциями над сходящимися последовательностями

I. Предположим, что последовательности и имеют конечные пределы.

Теорема 1. Если,,то

1) ,

2)

Доказательство.

По теореме 3 § 4 (необходимое и достаточное условие сходимости) ,, где,.

1) .

Так как - БМП (по теореме 1 и следствию 2 из § 4), то по теореме 3 § 4.

2)

- БМП по следствию 1 §4, - БМП по следствию 3 §4,-БМП по теореме 1 §4. Следовательно, по теореме 3 §4.

Следствие 1. Если и, то.

Следствие 2. Если и, то.

Теорема 2. 1)Пусть ,

2) ,.

Тогда .

Некоторые известные пределы: 1. , гдеa>0. 2. .

II. В теоремах 1 и 2 предполагалось, что последовательности (x_n) и (y_n) имеют конечные пределы и, кроме того, в теореме 2 . Теперь рассмотрим случай, когда последовательности могут быть, ББП, а в теореме 2- БМП.

1. Частное .

1) ,.

- БМП, так как - сходящаяся, а-БМП.

2) ,.

. Последовательность 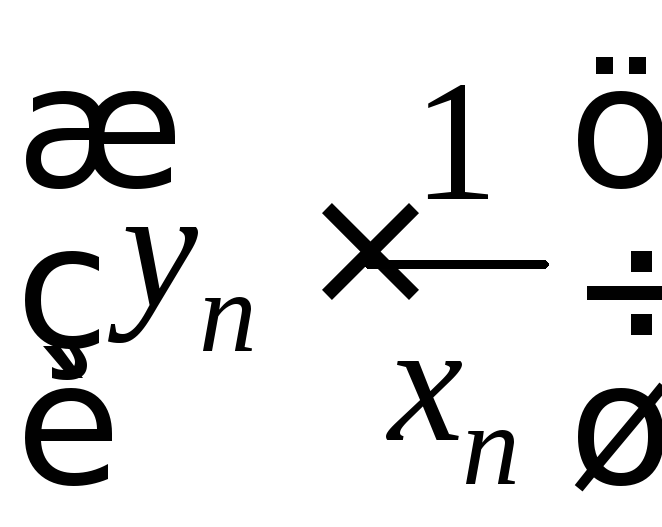- БМ, так как

- БМП, а - сходящаяся, значит,- ББП.

3) ,.

, - сходящаяся последовательность,- БМП.

Значит, БМП. Следовательно,- ББП.

4) ,(аналогично).

5) .

Рассмотрим примеры:

а) ,

б) ,

в) ,

г) не.

В этом случае имеем отношение двух БМП. Это отношение может иметь предел (конечный или бесконечный), а может и не иметь предела в зависимости от конкретного способа задания последовательностей и . Поэтому отношение двух БМП называетсянеопределенностью вида .

Если предел отношения найден или доказано, что он не существует, то говорят, что неопределенность раскрыта.

6)

- отношение двух ББП – неопределенность вида

2. Сумма .

1) ,,

2) ,,

3) ,-неопределенность вида .