
- •Введение в анализ
- •§1. Действительные числа
- •1. Понятие действительного числа
- •2. Модуль действительного числа и его свойства Определение. Модулем действительного числа а называется неотрицательное число, обозначаемое |а|, определяемое формулой:
- •Геометрический смысл: Пример 1.А);
- •По свойству 3
- •Число хнаходится от точкиана расстоянии меньшем, чемb.
- •3. Числовые множества. Промежутки. Окрестности
- •§ 2. Ограниченные и неограниченные множества. Верхние и нижние грани числовых множеств
- •§ 3. Предел последовательности
- •2. Предел последовательности. Пусть дана последовательность :(1)
- •3. Единственность предела
- •4. Ограниченность сходящейся последовательности
- •Доказательство.
- •5. Свойства сходящихся последовательностей
- •§ 4. Бесконечно малые последовательности
- •§ 5. Бесконечно большие последовательности (ббп)
- •§ 6. Свойства пределов, связанные с арифметическими операциями над сходящимися последовательностями
- •3. Произведение .
- •§7. Предел монотонной последовательности (признаки существования предела последовательности)
- •§ 8. Принцип вложенных отрезков
- •§ 9. Число е.
- •§10. Подпоследовательности
- •§11. Критерий Коши сходимости числовой последовательности
2. Модуль действительного числа и его свойства Определение. Модулем действительного числа а называется неотрицательное число, обозначаемое |а|, определяемое формулой:

Г еометрический
смысл модуля:
|
еометрический
смысл модуля:
|![]() |-
расстояние от точки 0 до точкиа
на числовой оси.
|-
расстояние от точки 0 до точкиа
на числовой оси.
Из определения модуля вытекают его свойства.
Cвойства модуля
1![]() .
|a|=|-a|.
.
|a|=|-a|.
![]() 1)
Пусть а>0.
Тогда |а|
= а. Если
а>0, то –а<0
и
1)
Пусть а>0.
Тогда |а|
= а. Если
а>0, то –а<0
и
![]() |-а|=-(-а)=а
|-а|=-(-а)=а
![]() |а|=|-а|=
а.
|а|=|-а|=
а.
2) Пусть а<0.
Тогда |а|=
-а.
Если а<0,
то -а>0
и
![]() |-а|=
-а
|-а|=
-а
![]() |а|=|-а|
= -а.
|а|=|-а|
= -а.
![]()
2![]() .
-|а|
.
-|а|![]() а
а![]() |а|.
|а|.
![]() I.
Докажем, что -|а|
I.
Докажем, что -|а|![]() а
а
а>0 . Тогда -|а| = -а, -а<а, то есть -|а|<а,
а<0. Тогда -|а|= -(-а). Итак, -|а| а.
Докажем, что а
 |а|
|а|
a>0. Тогда |а| = а и получаем равенство
a<0. Тогда |а| = -а, -а>0 и
 а <-а
a<|а|.
а <-а
a<|а|.
Итак,
в
любом случае
а![]() |а|.
|а|.![]()
3![]() .
.
![]() b
b![]() 0
неравенство |х|
0
неравенство |х|![]() b
равносильно -b
b
равносильно -b![]() х
х![]() b
(при b<0
неравенство |х|
b
(при b<0
неравенство |х|![]() b
не верно ни
при каком х).
b
не верно ни
при каком х).
![]() 1)
Докажем (1) |х|
1)
Докажем (1) |х|![]() b
b![]() -b
-b![]() х
х![]() b
(2).
b
(2).
(1)![]() -|х|
-|х|![]() -b.
По свойству
2
-b.
По свойству
2![]() -|х|
-|х|![]() х
х![]() |х|
|х|
![]() -b
-b![]() -|х|
-|х|![]() х
х![]() |х|
|х|![]() b,
то есть -b
b,
то есть -b![]() х
х![]() b.
b.
2) Докажем,
что (2)![]() (1).
(1).
И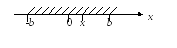 меем-b
меем-b![]() х
х![]() b.
Так как х
b.
Так как х![]() b
и b
b
и b![]() 0,
то-х
0,
то-х![]() b.
Но |х|
равен либо х,
либо –х
b.
Но |х|
равен либо х,
либо –х![]() |х|
|х|![]() b.
b.![]()
![]()
Геометрический смысл: Пример 1.А);
б)
|х|<![]() <x<7.
<x<7.![]()
4![]() .
.
![]() b
b![]() 0
|х|b
0
|х|b
 .
(если b<0,
то неравенство верно для любого х)
.
(если b<0,
то неравенство верно для любого х)
![]() 1)
Необходимость.
1)
Необходимость.
Имеем |х|![]() b.
b.
Если
![]() ,
то |х|=
,
то |х|=![]()
Если
![]() ,
то |х|=
,
то |х|=![]()
2 )
Достаточность.
)
Достаточность.
Имеем
 ,
но |х|=х
или |х|=-х
,
но |х|=х
или |х|=-х
![]() |х|
|х|![]() .
.![]()
Геометрический смысл:
Пример 2.
а)
 б)
б)
5![]() .
(неравенство треугольника) |а+b|
.
(неравенство треугольника) |а+b|![]() |а|+|b|
|а|+|b|
(Модуль суммы двух чисел не превосходит суммы модулей этих чисел).
![]() По свойству 2
По свойству 2![]() :
+
:
+![]()
![]()

По свойству
3![]()
![]() |а+b|
|а+b|![]() |а|+|b|.
|а|+|b|.
![]()
Замечание. С
помощью метода математической индукции
неравенство треугольника можно обобщить
![]() конечного числа слагаемых:
конечного числа слагаемых:
![]() .
.
![]() 1)
Для п=2
неравенство доказано.
1)
Для п=2
неравенство доказано.
2) Предположим, что оно верно для п=k . Докажем, что оно верно для п=k+1.
![]()
верно для п=к+1.
![]()
6![]() .
|а-b|
.
|а-b|![]() |а|+|b|
|а|+|b|
Доказательство
![]() из 5
из 5![]() заменойb
на -b.
заменойb
на -b.
7![]() .
|а-b||а|-|b|
.
|а-b||а|-|b|
![]()
![]()
![]()
![]()
![]()
8![]() .|а+b||а|-|b|
.|а+b||а|-|b|
Доказательство.
![]() из
7
из
7![]() заменойb
на -b.
заменойb
на -b.
Из 5![]() -8
-8![]()
![]()
9![]() .
.![]()
![]() По
свойству 7
По
свойству 7![]() |а-b||а|-|b|
|b-a||b|-|a|
или |а-b||b|-|a|
Умножим на (-1)
|а-b||а|-|b|
|b-a||b|-|a|
или |а-b||b|-|a|
Умножим на (-1)
-|а-b||а|-|b|
Получим:
![]() По свойству 3
По свойству 3![]()
![]() .
.![]()
10![]()
![]()

![]() Докажем
для произведения (частное аналогично).
Докажем
для произведения (частное аналогично).
Возможны 4 случая:
1)
![]()
2)
![]()
3)
![]() аналогично 2)
аналогично 2)
4)
![]() .
.![]()
11![]() .
.
![]()
П ример
3.а)
ример
3.а)
![]()
б)
![]()
в)![]()
![]()
12![]() . 1)
. 1)
![]()
2)
![]()
![]()
![]() 1)
1)![]()
![]() ,
,
2)![]()

![]() .
.![]()
Геометрический
смысл величины
![]() .
.
![]() - расстояние между
точками а и
b
на числовой прямой.
- расстояние между
точками а и
b
на числовой прямой.
Г еометрический
еометрический
смысл неравенства
![]() .
.
По свойству 3
![]() -b<x-a<b
-b<x-a<b
a-b<x<a+b
![]() .
.
Число хнаходится от точкиана расстоянии меньшем, чемb.
3. Числовые множества. Промежутки. Окрестности
Определение. Числовое множество- множество, элементами которого являются действительные числа.
Примеры числовых множеств.
![]() .
.
Отрезок (сегмент, замкнутый промежуток)

Интервал (открытый промежуток)

Полуинтервалы
 ,
,
1)-3) называются
промежутками и обозначаются
![]() .
.
Бесконечные промежутки:
![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]() - вся числовая
прямая.
- вся числовая
прямая.
Окрестность точки
Пусть
![]()
Определение 1.
окрестностью
точки а называется
![]() интервал, содержащий точкуа.
Обозначается V(a).
интервал, содержащий точкуа.
Обозначается V(a).
 Определение
2.
Определение
2.![]() -окрестностью
точки а
-называется
интервал, с центром в точке
а и
радиусом
-окрестностью
точки а
-называется
интервал, с центром в точке
а и
радиусом
![]() .
Обозначается
V(a;).
.
Обозначается
V(a;).
V(a;)=(a-;a+)
или
V(a;)=![]() ,
V(a;)=
,
V(a;)=![]() .
.
У каждой точки
![]() существует бесконечно много
существует бесконечно много
![]() -окрестностей.
-окрестностей.
Если
![]() ,
то
,
то![]() .
Но среди
.
Но среди
![]() -окрестностей
нет самой маленькой.
-окрестностей
нет самой маленькой.
Любые две различные
точки имеют непересекающиеся
![]() -окрестности.
-окрестности.
Пусть
![]() .
.
Возьмём
![]() .
Например, положим
.
Например, положим![]() .
.
Тогда


![]() (так как
(так как
![]() )
)![]() .
.
Определение 3.
Проколотой
![]() -окрестностью
точки а
называется
-окрестностью
точки а
называется
![]()
 -окрестность
без точки а.
-окрестность
без точки а.
Обозначается
![]()
![]()

![]()
![]() =
=![]()
Определение 4.
![]() -
-
![]() -окрестность
точки +
-окрестность
точки +![]() ,
,
![]() -
-
![]() -окрестность
точки -
-окрестность
точки -![]() ,
,
![]()
![]() -
-
![]() -окрестность
точки
-окрестность
точки![]() .
.
 Определение
5.Односторонние
окрестности точки а:
Определение
5.Односторонние
окрестности точки а:
![]() - левая
проколотая
- левая
проколотая
![]() -окрестность
точки
а,
-окрестность
точки
а,
![]() - правая
проколотая
- правая
проколотая
![]() -окрестность
точки а.
-окрестность
точки а.
В дальнейшем будем
рассматривать только
![]() -окрестности.
Будем называть их просто окрестностями.
-окрестности.
Будем называть их просто окрестностями.
