- •Экзамен по матану
- •1) Частные виды матриц.
- •2) Определители. Правила вычисления
- •3) Свойства определителей
- •4) Обратная матрица, вычисление, приложение.
- •5)Теорема о существовании и единственности обратной матрицы.
- •6) Теорема Кронекера – Капели
- •7) Метод крамера (вывод) решения систем линейных уравнений.
- •8)Метод Гаусса решения систем линейных уравнений
- •9) Решение неопределённых систем линейных уравнений.
- •10) Однородные системы линейных уравнений
- •11. Векторы. Линейные операции над векторами
- •12. Скалярное произведение векторов, свойства, приложения.
- •13. Векторное произведение векторов
- •14.Смешанное произведение векторов
- •15.Прямая линия на плоскости, её общее уравнение и его исследование.
- •16.Вывести параметрическое и каноническое уравнение прямой на плоскости.
- •17.Общее уравнение плоскости вывод исследование
- •18.Эллипс, гипербола парабола. Каноническое уравнение.
- •19.Каноническое и общее уравнение прямой в пространстве
- •20.Цилиндрические и канонические поверхности
- •21. Теорема о разности между переменной и её пределом ( Основная т. О пределах)
- •22.Теорема о связи бесконечно больших и бесконечно малых величин
- •23.Первый замечательный предел
- •24.Сравнение бесконечно малых функция и свойства эквивалентных
- •25.Точки разрыва и их классификации
- •26.Теоремы о производных суммы, произведения и частного двух функций.
- •27.Вывод производных тригонометрических функций sincostgctg
- •28 Производная обратной функции
- •29.Вывод производной и логарифмический показатель функции (axиlogax)
- •31. Производная неявной функции. Производная функции заданной параметрически.
- •32.Теорема ферма
- •33.Теорема Роля
- •34.Теорема Коши
- •35. Теорема Лопиталя
- •36. Раскрытие неопределённости вида 0*∞, ∞-∞, 1∞
- •37. Условие монотонности. Необходимое условие экстремума.
24.Сравнение бесконечно малых функция и свойства эквивалентных
Пусть
![]() и
и![]() – бесконечно малые функции при
– бесконечно малые функции при![]() .
Предел отношения этих величин может
принимать любые значения – в зависимости
от быстроты убывания одной величины
относительно другой. Для сопоставления
скоростей убывания этих величин при
стремлении x точке a можно использовать
предел отношения
.
Предел отношения этих величин может
принимать любые значения – в зависимости
от быстроты убывания одной величины
относительно другой. Для сопоставления
скоростей убывания этих величин при
стремлении x точке a можно использовать
предел отношения
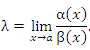
Если этот предел
представляет собой конечное ненулевое
число, то
![]() и
и![]() называются бесконечно малыми одного и
того же порядка.
Особый интерес
представляет частный случай, когда λ =
1. Тогда говорят, что
называются бесконечно малыми одного и
того же порядка.
Особый интерес
представляет частный случай, когда λ =
1. Тогда говорят, что![]() и
и![]() являются эквивалентными бесконечно
малыми при
являются эквивалентными бесконечно
малыми при![]() и
записывают это утверждение в виде
и
записывают это утверждение в виде
![]()
Если λ = 0, то
говорят, что
![]() является бесконечно малой более высокого
порядка по сравнению с
является бесконечно малой более высокого
порядка по сравнению с![]() при
при![]() а функция
а функция![]() имеет меньший порядок малости.
Термин “порядок малости” допускает
уточнение, если
имеет меньший порядок малости.
Термин “порядок малости” допускает
уточнение, если![]() и
и![]() представляют собой бесконечно малые
одного и того же порядка. В этом случае
говорят, что
представляют собой бесконечно малые
одного и того же порядка. В этом случае
говорят, что![]() является бесконечно малой n-го порядка
по сравнению с
является бесконечно малой n-го порядка
по сравнению с![]() .
Например, функция
.
Например, функция![]() является бесконечно малой 4-го порядка
по сравнению с
является бесконечно малой 4-го порядка
по сравнению с![]() при x → 0.
Если λ = ∞, то бесконечно
малые
при x → 0.
Если λ = ∞, то бесконечно
малые![]() и
и![]() как бы меняются своими ролями. В этом
случае функция
как бы меняются своими ролями. В этом
случае функция![]() является бесконечно малой более высокого
порядка по сравнению с
является бесконечно малой более высокого
порядка по сравнению с![]() при
при![]() .
Сформулируем некоторые полезные
свойства эквивалентных бесконечно
малых.
.
Сформулируем некоторые полезные
свойства эквивалентных бесконечно
малых.
Если
![]() и
и![]() – эквивалентные бесконечно малых при
– эквивалентные бесконечно малых при![]() то их разность есть бесконечно малая
более высокого порядка. Действительно,
то их разность есть бесконечно малая
более высокого порядка. Действительно,![]()
Для записи
такого утверждения используется
выражение
![]()
Бесконечно
малые
![]() и
и![]() являются эквивалентными, если
являются эквивалентными, если![]() и
и![]() являются бесконечно малыми одного и
того же порядка. Если
являются бесконечно малыми одного и
того же порядка. Если![]() – бесконечно малая более высокого
порядка по сравнению с
– бесконечно малая более высокого
порядка по сравнению с![]() при
при![]() то
то![]()
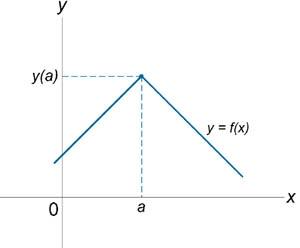
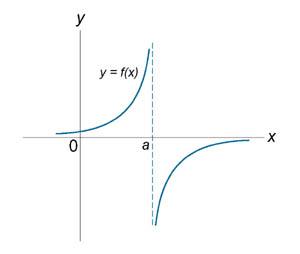
25.Точки разрыва и их классификации
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
|
|
|
|
|
Непрерывна при x = a. |
|
Имеет разрыв при x = a. |
|
|
|
|
|
Непрерывна при x = a. |
|
Имеет разрыв при x = a. |
|
Рисунок 1. | ||
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Существуют
левосторонний предел
![]() и
правосторонний предел
и
правосторонний предел![]() ;
;
Эти односторонние пределы конечны.
При этом возможно следующие два случая:
Левосторонний предел и правосторонний предел равны друг другу:
![]()
Такая точка называется точкой устранимого разрыва.
Левосторонний предел и правосторонний предел не равны друг другу:
![]()
Такая точка
называется точкой конечного разрыва.
Модуль разности значений односторонних
пределов
![]() называется
скачком функции.
называется
скачком функции.
Функция f (x) имеет точку разрыва второго рода при x = a , если, по крайней мере, один из односторонних пределов не существует или равен бесконечности.
26.Теоремы о производных суммы, произведения и частного двух функций.
Пусть функции
u = u(x), v= v(x) дифференцируемы. Тогда
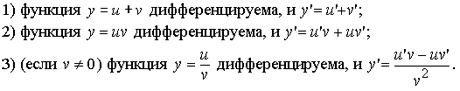
Доказательство
Если аргумент x получит приращение Δx, то функции u, v получат приращения
![]()
Пусть y = u + v,
тогда
![]()
Воспользовавшись свойством предела суммы функции, получаем
![]()
Утверждение 1) теоремы доказано.
Если y = u v, то
![]() Прибавив
и отняв в правой части этого равенства
произведение
Прибавив
и отняв в правой части этого равенства
произведение![]() ,
после перегруппировки слагаемых получим
,
после перегруппировки слагаемых получим![]() .
Воспользовавшись свойствами предела
функции, получаем
.
Воспользовавшись свойствами предела
функции, получаем

Утверждение 2) теоремы доказано.
Теперь, если
![]()
Прибавив и
отняв в правой части этого равенства
частное
![]() ,
после перегруппировки слагаемых получим
,
после перегруппировки слагаемых получим
![]()
Далее аналогично доказываем утверждение 3). Теорема доказана.
Из теорем 2,3 следует, что постоянную можно выносить за знак производной, т.е. (cy)' = cy'