32.Теорема ферма

33.Теорема Роля

Если функция f(x) непрерывна на замкнутом интервале [а, b], имеет внутри интервала производную и если

f(a) = f(b)

то внутри интервала [а, b] найдется хотя бы одно такое значение x0 (a < x0 < b), что

f ' (x0) = 0.

Доказательство. Рассмотрим два случая. 1. Функция f(x) постоянна на интервале [а, b]; тогда f ' (x) = 0 для любого x (a < x < b), т.е. утверждение теоремы Ролля выполняется автоматически. 2. Функция f(x) не является постоянной (Рисунок 1); тогда наибольшего или наименьшего или обоих этих значений она достигает во внутренней точке интервала, ибо f(b) = f(a), и если f(a) - наименьшее значение, то наибольшее значение значение функция f(x) примет внутри интервала.

Рис.1

Пусть например f(x0) - наибольшее значение функции f(x) на интервале [а, b] и x0 - внутренняя точка этого интервала. Тогда f(x0) является максимумом функции: f(x0) і f(x) для всех x из достаточно малой окрестности x0 [за эту окрестность можно впрочем, взять интервал (а, b)].
Так как, по условию, f(x) имеет в точке x0 производную, то по теореме о необходимом признаке экстремума,

f ' (x0) = 0,

и теорема Ролля доказана.

34.Теорема Коши

Если функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b) и g¢(x) ¹ 0 на интервале (a, b), то существует по крайней мере одна точка e, a < e < b, такая, что

.

Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке e.

Для доказательства этой теоремы на первый взгляд очень удобно воспользоваться теоремой Лагранжа. Записать формулу конечных разностей для каждой функции, а затем разделить их друг на друга. Однако, это представление ошибочно, т.к. точка e для каждой из функции в общем случае различна. Конечно, в некоторых частных случаях эта точка интервала может оказаться одинаковой для обеих функций, но это- очень редкое совпадение, а не правило, поэтому не может быть использовано для доказательства теоремы.

Доказательство. Рассмотрим вспомогательную функцию

,

которая на интервале [a, b] удовлетворяет условиям теоремы Ролля. Легко видеть, что при х = а и х = b F(a) = F(b) = 0. Тогда по теореме Ролля существует такая точка e,

a < e < b, такая, что F¢(e) = 0. Т.к.

, то

А т.к., то

35. Теорема Лопиталя

Если функции иобладают следующим набором условий:

или;

;

в некоторой окрестности точки,

тогда существует . При этом теорема верна и для других баз (для указанной будет приведено доказательство).

Докажем теорему для случая, когда пределы функций равны нулю (т. н. неопределённость вида ).

Поскольку мы рассматриваем функции итолько в правой проколотой полуокрестности точки, мы можем непрерывным образом их доопределить в этой точке: пусть. Возьмём некоторыйиз рассматриваемой полуокрестности и применим к отрезкутеорему Коши. По этой теореме получим:

,

но , поэтому.

Дальше, записав определение предела отношения производных и обозначив последний через , из полученного равенства выводим:

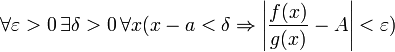для конечного предела и

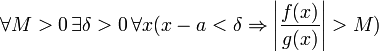для бесконечного,

что является определением предела отношения функций.

2. Докажем теорему для неопределённостей вида .

Пусть, для начала, предел отношения производных конечен и равен . Тогда, при стремленииксправа, это отношение можно записать как, где— O(1). Запишем это условие:

.

Зафиксируем из отрезкаи применим теорему Коши ко всемиз отрезка:

, что можно привести к следующему виду:

.

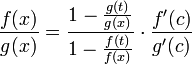Для , достаточно близких к, выражение имеет смысл; предел первого множителя правой части равен единице (так каки— константы, аистремятся к бесконечности). Значит, этот множитель равен, где— бесконечно малая функция при стремленииксправа. Выпишем определение этого факта, используя то же значение, что и в определении для:

.

Получили, что отношение функций представимо в виде , и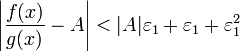. По любому данномуможно найти такое, чтобы модуль разности отношения функций ибыл меньше, значит, предел отношения функций действительно равен.

Если же предел бесконечен (допустим, он равен плюс бесконечности), то

.

В определении будем брать; первый множитель правой части будет больше 1/2 при, достаточно близких к, а тогда.

Для других баз доказательства аналогичны приведённым.