
- •Экзамен по матану
- •1) Частные виды матриц.
- •2) Определители. Правила вычисления
- •3) Свойства определителей
- •4) Обратная матрица, вычисление, приложение.
- •5)Теорема о существовании и единственности обратной матрицы.
- •6) Теорема Кронекера – Капели
- •7) Метод крамера (вывод) решения систем линейных уравнений.
- •8)Метод Гаусса решения систем линейных уравнений
- •9) Решение неопределённых систем линейных уравнений.
- •10) Однородные системы линейных уравнений
- •11. Векторы. Линейные операции над векторами
- •12. Скалярное произведение векторов, свойства, приложения.
- •13. Векторное произведение векторов
- •14.Смешанное произведение векторов
- •15.Прямая линия на плоскости, её общее уравнение и его исследование.
- •16.Вывести параметрическое и каноническое уравнение прямой на плоскости.
- •17.Общее уравнение плоскости вывод исследование
- •18.Эллипс, гипербола парабола. Каноническое уравнение.
- •19.Каноническое и общее уравнение прямой в пространстве
- •20.Цилиндрические и канонические поверхности
- •21. Теорема о разности между переменной и её пределом ( Основная т. О пределах)
- •22.Теорема о связи бесконечно больших и бесконечно малых величин
- •23.Первый замечательный предел
- •24.Сравнение бесконечно малых функция и свойства эквивалентных
- •25.Точки разрыва и их классификации
- •26.Теоремы о производных суммы, произведения и частного двух функций.
- •27.Вывод производных тригонометрических функций sincostgctg
- •28 Производная обратной функции
- •29.Вывод производной и логарифмический показатель функции (axиlogax)
- •31. Производная неявной функции. Производная функции заданной параметрически.
- •32.Теорема ферма
- •33.Теорема Роля
- •34.Теорема Коши
- •35. Теорема Лопиталя
- •36. Раскрытие неопределённости вида 0*∞, ∞-∞, 1∞
- •37. Условие монотонности. Необходимое условие экстремума.
18.Эллипс, гипербола парабола. Каноническое уравнение.
Алгебраической кривой второго порядка называется кривая Г, уравнение которой в декартовой системе координат имеет вид:
Аx2 + 2Вxy + Сy2 + 2Dx + 2Еy + F = 0,
где не все коэффициенты А, В и С равны одновременно нулю.
Если кривая Г невырожденная, то для неё найдется такая декартова прямоугольная система координат, в которой уравнение этой кривой примет один из следующих трех видов (каноническое уравнение):
![]() - эллипс,
- эллипс,
![]() - гипербола,
- гипербола,
![]() px
- парабола.
px
- парабола.
Эллипс –
геометрическое множество точек плоскости,
сумма расстояний от которых до двух
точек
![]() и
и![]() ,
называемых фокусами, есть величина
постоянная 2a, большая, чем расстояние
между фокусами 2c:
,
называемых фокусами, есть величина
постоянная 2a, большая, чем расстояние
между фокусами 2c:![]() .
.
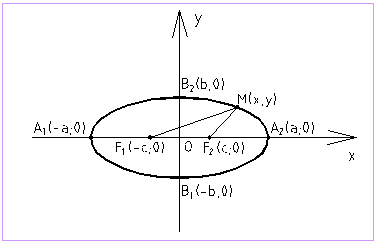
Эллипс,
заданный каноническим уравнением:![]()
симметричен
относительно осей координат. Параметры
а и b называются полуосями эллипса
(большой и малой соответственно), точки
![]() ,
,![]() ,
,![]() ,
,![]() называются его вершинами.
называются его вершинами.
Если а>b, то
фокусы находятся на оси ОХ на расстоянии
![]() от центра эллипса О.
от центра эллипса О.
Число
![]() (
(![]() )
)
называется
эксцентриситетом эллипса и является
мерой его «сплюснутости» (при
![]() эллипс является окружностью, а при
эллипс является окружностью, а при![]() он вырождается в отрезок длиною
он вырождается в отрезок длиною![]() ).
).
Если а<b, то
фокусы находятся на оси ОY и
![]() ,
,![]() .
.
Гипербола –
геометрическое множество точек плоскости,
модуль разности расстояний от которых
до двух точек
![]() и
и![]() ,
называемых фокусами, есть величина
постоянная 2a, меньшая, чем расстояние
между фокусами 2c:
,
называемых фокусами, есть величина
постоянная 2a, меньшая, чем расстояние
между фокусами 2c:![]() .
.
Г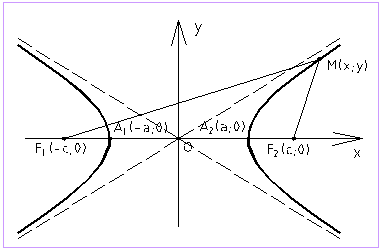 ипербола,
заданная каноническим уравнением:
ипербола,
заданная каноническим уравнением:
![]()
симметрична
относительно осей координат. Она
пересекает ось ОХ в точках
![]() и
и![]() - вершинах гиперболы, и не пересекает
оси ОY.
- вершинах гиперболы, и не пересекает
оси ОY.
Параметр а называется вещественной полуосью, b – мнимой полуосью.
Число
![]() ,
(
,
(![]() )
)
называется эксцентриситетом гиперболы.
Прямые
![]() называются асимптотами гиперболы.
называются асимптотами гиперболы.
Гипербола,
заданная каноническим уравнением :
![]() ( или
( или![]() ),
),
называется
сопряжённой ( имеет те же асимптоты ).
Её фокусы расположены на оси OY. Она
пересекает ось ОY в точках
![]() и
и![]() - вершинах гиперболы, и не пересекает
оси ОX.
- вершинах гиперболы, и не пересекает
оси ОX.
В этом случае
параметр b называется вещественной
полуосью, a – мнимой полуосью. Эксцентриситет
вычисляется по формуле:
![]() ,
(
,
(![]() ).
).
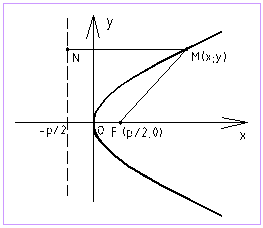
Парабола – множество точек плоскости, равноудаленных от данной точки F, называемой
фокусом, и
данной прямой, называемой директрисой:
![]() .
.
Парабола, заданная указанным каноническим уравнением, симметрична относительно оси ОХ.
Уравнение
![]() задает параболу, симметричную относительно
оси ОY.
задает параболу, симметричную относительно
оси ОY.
Парабола
![]() имеет фокус
имеет фокус![]() и директрису
и директрису![]() .
.
Парабола
![]() имеет фокус
имеет фокус![]() и директрису
и директрису![]() .
.
Если р>0, то в обоих случаях ветви параболы обращены в положительную сторону соответствующей оси, а если р<0 – в отрицательную сторону.
19.Каноническое и общее уравнение прямой в пространстве
Прямая в пространстве может быть задана:
1) как линия пересечения двух плоскостей,т.е. системой уравнений:
A 1 x + B 1 y + C 1 z + D 1 = 0, A 2 x + B 2 y + C 2 z + D 2 = 0; (3.2)
2) двумя своими точками M 1 (x 1, y 1, z 1 ) и M 2 (x 2, y 2, z 2 ), тогда прямая, через них проходящая, задается уравнениями:
![]() =
=![]() ;
(3.3)
;
(3.3)
3) точкой M 1 (x 1, y 1, z 1 ), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:
![]() .
(3.4)
.
(3.4)
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор aназывается направляющим вектором прямой.
Решая систему (3.2) как систему линейных уравнений относительно неизвестных x и y, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой :
x = mz + a, y = nz + b. (3.6)
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:
![]() .
.
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n = [ n 1, n 2 ], где n 1 (A 1, B 1, C 1 ) и n 2 (A 2, B 2, C 2 ) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система
![]()
равносильна
системе
![]() ;
такая прямая перпендикулярна к оси Ох.
;
такая прямая перпендикулярна к оси Ох.
Система
![]() равносильна системе x = x 1, y = y 1 ; прямая
параллельна оси Oz.
равносильна системе x = x 1, y = y 1 ; прямая
параллельна оси Oz.
