16.Вывести параметрическое и каноническое уравнение прямой на плоскости.

Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy. Поставим себе задачу: получить уравнение прямой a, если- некоторая точка прямой a и- направляющий вектор прямой a.

Пусть - плавающая точка прямой a. Тогда векторявляется направляющим вектором прямой a и имеет координаты. Очевидно, что множество всех точекна плоскости определяют прямую, проходящую через точкуи имеющую направляющий вектортогда и только тогда, когда векторыиколлинеарные.

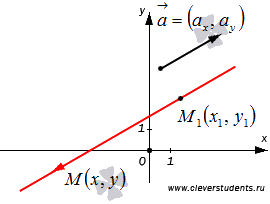
Запишем необходимое и достаточное условие коллинеарности векторов и:. Последнее равенство в координатной форме имеет вид.

Если и, то мы можем записать

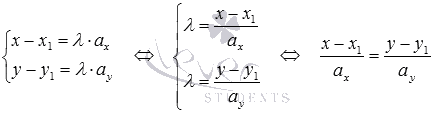
Полученное уравнение вида 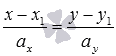называют каноническим уравнением прямой на плоскости в прямоугольной системе координат Oxy. Уравнение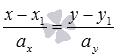также называют уравнением прямой в каноническом виде.

Итак, каноническое уравнение прямой на плоскости вида 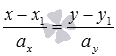задает в прямоугольной системе координат Oxy прямую линию, проходящую через точкуи имеющую направляющий вектор.

Параметрическим уравнением прямой являеться:

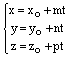,, (7)

где – координаты произвольной фиксированной точки данной прямой,– соответствующие координаты произвольного направляющего вектора данной прямой, t – параметр.

Доказательство. В соответствии с определением уравнения любого множества точек координатного пространства, мы должны доказать, что уравнениям (7) удовлетворяют все точки прямой L и, с другой стороны, не удовлетворяют координаты точки не лежащей на прямой.

Пусть произвольная точка . Тогда векторыиявляются по определению коллинеарными и по теореме о коллинеарности двух векторов следует, что один из них линейно выражается через другой, т.е. найдется такое число, что. Из равенства векторовиследует равенство их координат:

,,, ч.т.д.

Обратно, пусть точка . Тогдаи по теореме о коллинеарности векторов ни один из них не может быть линейно выражен через другой, т.е.и хотя бы одно из равенств (7) не выполняется. Таким образом, уравнениям (7) удовлетворяют координаты только тех точек, которые лежат на прямой L и только они, ч.т.д.

Теорема доказана.

Следствие. Следующая система уравнений является уравнениями прямой:

. (8)

Доказательство. Выразив параметр t из уравнений (7), получаем:

,,, (9)

откуда и следуют уравнения (8). Ясно, что системы уравнений (7) и (8) равносильны, т.е. их множества решений совпадают и система (8), так же как и система (7), являются уравнениями прямой, ч.т.д.

17.Общее уравнение плоскости вывод исследование

Всякое уравнение вида , где A, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в заданной прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве определяется уравнением видапри некотором наборе чисел A, B, C и D.

Теорема состоит из двух частей. В первой части нам дано уравнениеи нужно доказать, что оно определяет плоскость. Во второй части, нам дана некоторая плоскость и требуется доказать, что ее можно определить уравнениемпри некотором выборе чисел А, В, С и D.

Начнем с доказательства первой части теоремы.

Так как числа А, В и С одновременно не равны нулю, то существует точка , координаты которой удовлетворяют уравнению, то есть, справедливо равенство. Отнимем левую и правую части полученного равенства соответственно от левой и правой частей уравнения, при этом получим уравнение видаэквивалентное исходному уравнению. Теперь, если мы докажем, что уравнениеопределяет плоскость, то этим будет доказано, что эквивалентное ему уравнениетакже определяет плоскость в заданной прямоугольной системе координат в трехмерном пространстве.

Равенство представляет собой необходимое и достаточное условие перпендикулярности векторови. Иными словами, координаты плавающей точкиудовлетворяют уравнениютогда и только тогда, когда перпендикулярны векторыи. Тогда, учитывая факт, приведенный перед теоремой, мы можем утверждать, что если справедливо равенство, то множество точекопределяет плоскость, нормальным вектором которой является, причем эта плоскость проходит через точку. Другими словами, уравнениеопределяет в прямоугольной системе координат Oxyz в трехмерном пространстве указанную выше плоскость. Следовательно, эквивалентное уравнениеопределяет эту же плоскость. Первая часть теоремы доказана.

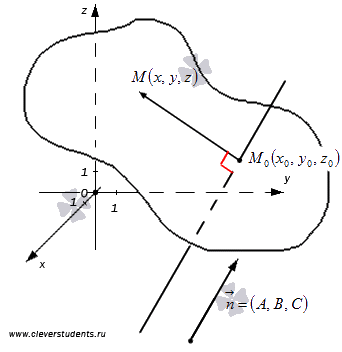
Приступим к доказательству второй части.

Пусть нам дана плоскость, проходящая через точку , нормальным вектором которой является. Докажем, что в прямоугольной системе координат Oxyz ее задает уравнение вида.

Для этого, возьмем произвольную точку этой плоскости. Пусть этой точкой будет . Тогда векторыибудут перпендикулярны, следовательно, их скалярное произведение будет равно нулю:. Приняв, уравнение примет вид. Это уравнение и задает нашу плоскость. Итак, теорема полностью доказана.