34.Формула Грина

формула устанавливает связь между криволинейными и двойными интегралами.

Пусть имеется некоторая правильная замкнутая область Д, ограниченная контуром L и пущая ф-ции P(x,y) и Q(x,y) непрерывны вместе со своими частными производными: в данной области. тогда имеет место ф-ла:

И вот вся эта фигулина и есть формула Грина.

Контур L определяющий область д может быть задан показательными уравнениями х = х1(у), х=х2(у) с<=y<=d x1(y)<=x2(y) или

y = y1(x), y=y2(x) a<=x<=b y1(x)<=y2(x).

Рассмотрим область Д ограниченную неравенствами: a<=x<=b и y1(x)<=y2(x). и преобразуем двойной интеграл к криволинейным для чего сведем его к повторному и ф-ле Невтона-Лыебница выполним интегрирование по у и получим:

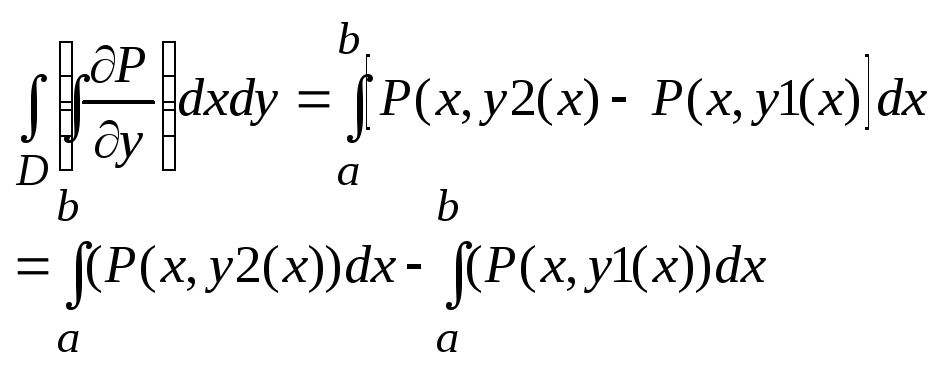каждый из 2 определенных интегралов в правой части последнего равенства = криволинейному интегралу 2 рода взятому по соответствующей кривой а именно:

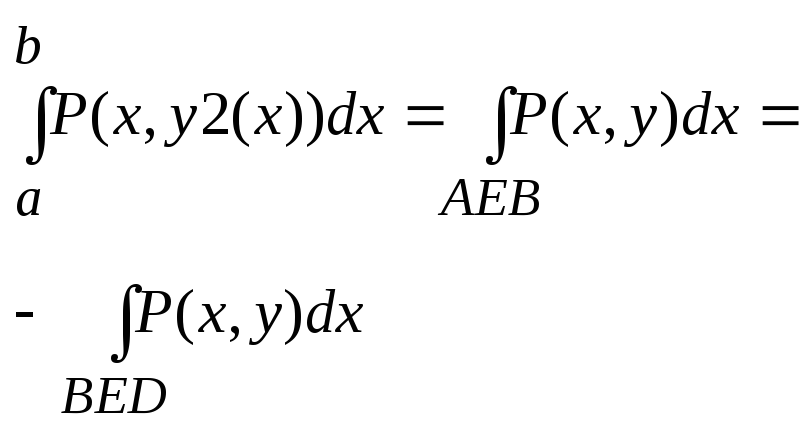
Итак двойной интеграл:

Формула Грина остается справедливой для всякой замкнутой области Д, которую можно разбить проведением дополнительных линий на конечной число правильных замкнутых областей.

35.Теорема Стокса

одна из основных теорем дифференциальной геометрии и математического анализа об интегрировании дифференциальных форм, которая обобщает несколько теорем анализа.

Пусть S является гладкой поверхностью, ограниченной гладкой кривой C. Тогда для любой непрерывно дифференцируемой векторной функции справедлива теорема Стокса:( гдеn единичный вектор нормали к поверхности S, направление которого таково, что при обходе контура l = dS поверхность S остается слева.)

где − ротор векторного поляF. Символ показывает, что криволинейный интеграл вычисляется по замкнутой кривой.

Будем предполагать, что ориентация поверхности и направление обхода кривой соответствуют правилу правой руки. В этом случае при обходе кривой поверхность всегда остается слева, если голова направлена в ту же сторону, что и вектор нормали n.

Теорема Стокса связывает между собой криволинейные интегралы второго рода и поверхностные интегралы второго рода.

В координатной форме теорема Стокса может быть записана в следующем виде:

36.Формула Остроградского

Фо́рмула Острогра́дского — формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, замкнутого под поверхностью: ( где дV = S - внешняя сторона поверхности, ограничивающей тело V;n - единичный вектор внешней нормали к ней.)то есть интеграл от дивергенции векторного поля F, распространённый по некоторому объёму T, равен потоку вектора через поверхность S, ограничивающую данный объём.

Формула применяется для преобразования объёмного интеграла в интеграл по поверхности, ограничивающей данный объём, то есть замкнутых, таких как поверхность воздушного шарика, и не применима к поверхностям, таким как воздушный шар с подогревом.

В работе Остроградского формула записана в следующем виде: где ω и s — дифференциалы объёма и поверхности соответственно.

37.Скалярным полем

называется плоская или пространственная область, с каждой точкой М которой связано определенное зна­чение некоторой скалярной физической величины и=и(М). Задание поля скалярной величины и равносильно заданию скалярной (числовой) функции и (М).

Функция и(М), определяющая плоское скалярное поле, как функция точки М(х,у), зависит от двух переменных и=и(х,у), а функция, определяющая пространственное скалярное поле,

как функция точки М (х,у,z), зависит от трех переменных и=и(х, у, z).

Линией уровня плоского скалярного поля называется совокуп­ность точек плоскости, в которых функция этого поля имеет одинаковые значения. Линия уровня, во всех точках которой функция поля и (х, у) имеет одно и то же значение С, опреде­ляется уравнением и(х, у) = С; различным постоянным значе­ниям С_1, С₂, С₃, ... функции поля соответствуют различные линии уровня: и(х, у) = С₁, и(х, у)=С₂, и(х, у)=С₃, ...