28. Замена переменных в тройном интеграле.

Если ограниченная замкнутая область пространства V = f(x,y,z) взаимно однозначно отображается на область V’ пространства = (u,v,w) Если непрерывно дифференцируемы функции: x=x(u,v,w), y=y(u,v,w), z=z(u,v,w) и существует якобиан

то справедлива формула:

При переходе к цилиндрическим координатам, с вязанными с x,y,z формулами: x=rcos, y=rsin, z=z (0<=r<=+, 0<= <= 2, -<=z<=+)

Якобиан преобразования:

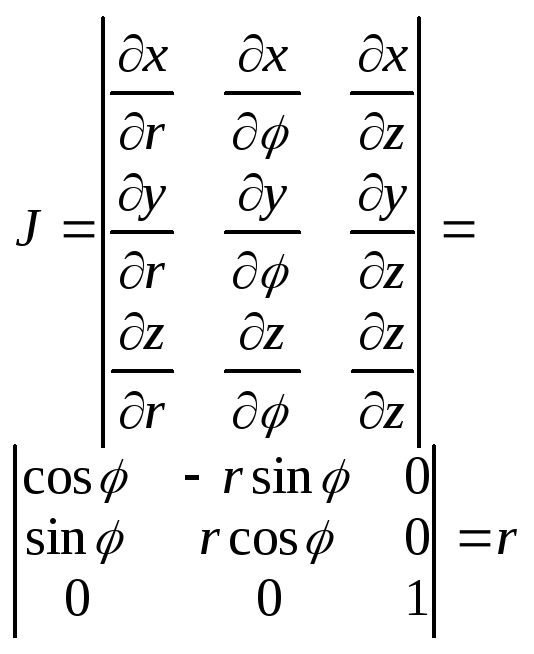И поэтому в цилиндрических координатах переход осуществляется так: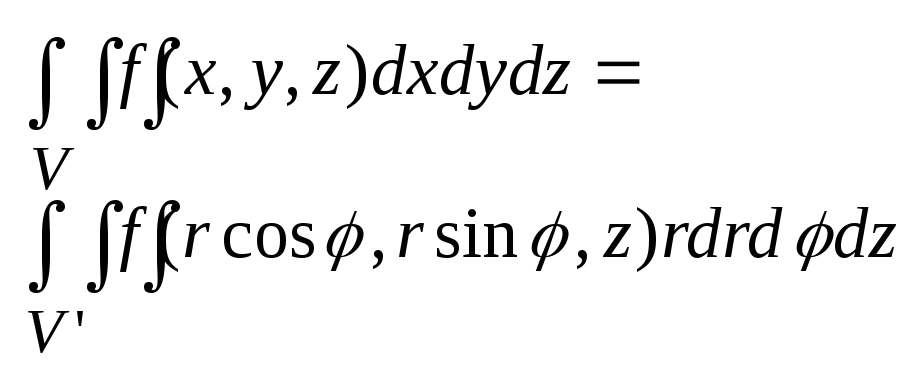При переходе к сферическим координатам:r?  , связанными с z,y,z формулами x=rsincos,

y=r sinsin, z=rcos.

(0<=r<=+, 0<= <= 2,

0<= <=2)

Якобиан преобразования:

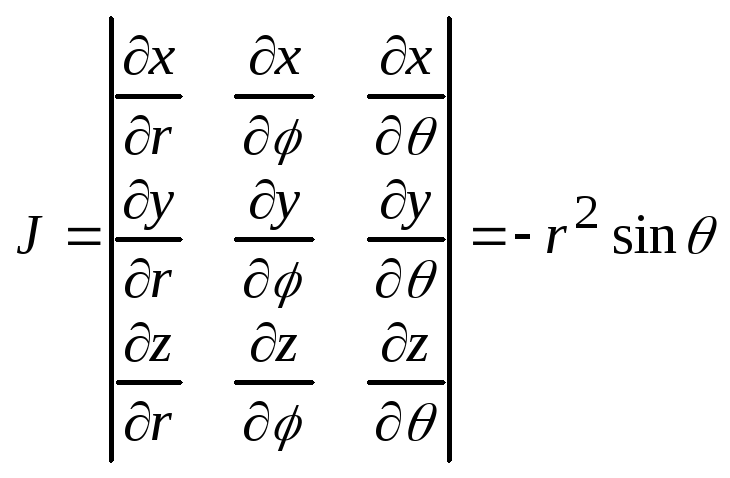
Т. е. |J|=r²sin.

Итак, в сферических координатах сие будет:

29. Свойства криволинейных интегралов

Пусть l — гладкая, без особых точек и самопересечений кривая (допускается одно самопересечение — случай замкнутой кривой), заданная параметрически. (отрезок параметризации) – рассматриваем часть кривой. Пусть– разбиение отрезка параметризации, причем. Зададим разбиение кривой

За l_k обозначим часть кривой от точки M_k до точки,.Введем мелкость разбиения отрезка параметризацииθ: Введем набор промежуточных точек разбиения отрезка параметризации l:Зададим набор промежуточных точек разбиения кривойПусть нам также даны 4 функции, которые определены вдоль кривой l:Рассмотрим 4 интегральные суммы.

1) Интегральная сумма криволинейного интеграла первого рода:

2) Три интегральных суммы криволинейного интеграла второго рода:

Если, то говорят, что функция f интегрируема в смысле криволинейного интеграла первого рода по кривой l, а сам предел называют криволинейным интегралом первого рода функции f по кривой l и обозначают. Здесьdl — дифференциал кривой.

Если,, то говорят, что функции P, Q и R интегрируемы в смысле криволинейного интеграла второго рода по кривой l, а сами пределы называют криволинейными интегралами второго рода функций P, Q и R по кривой l и обозначаютСумму криволинейных интегралов второго рода функций P, Q и R также называют криволинейным интегралом второго рода вектор-функциии обозначают:

Св-ва криволинейных интегралов 1 рода:

1.Константа выносится за знак интеграла, а интеграл суммы можно представить в виде суммы интегралов:

2. Если дуга АВ состоит из двух дуг Ас и Св не имеющих общих внутренних точек и если для ф-ции f(x,y) сущ криволинейный интеграл по АВ, то для для сей ф-ции сущ криволинейные интегралы по АС и по ВС причем:

3.

4.Ф-ла среднего значения

если ф-ция f(x,y) непрерывна вдоль кривой АВ, то на этой кривой найдется точка М, такая, что:

, где l – длина кривой

Криволинейный интеграл 2 рода обладает всеми свойствами интегралов 1 рода, и ещё при изменении направления прохождения кривой он меняет знак.

5. Изменение направления обхода кривой интегрирования не влияет на знак интеграла:

6. Криволинейный интеграл первого рода не зависит от параметризации кривой.

30.Вычисление криволинейного интеграла

Пусть l — гладкая,спрямляемая кривая, заданная параметрически (как в определении). Пусть функция f(x,y,z) определена и интегрируема вдоль кривой l в смысле криволинейного интеграла первого рода. Тогда Здесь точкой обозначена производная по t: